[ 통계 ] Bias, Variance, MSE

개요

이번 포스팅에서는 통계학에서 자주 등장하지만 헷갈리는 용어들을 정리하고 알아보려고 한다. 통계학이나 머신러닝을 공부하다보면, bias, variance, residual, error 등의 용어들을 많이 접할 수 있다. 모두 비슷한 것처럼 알고 있지만 모두 다른 의미를 가지고 있다. 그래서 이번 포스팅에서는 각각의 용어들을 정리하고 이와 연관된 개념들을 알아볼 것이다.

Bias

Bias는 한 마디로 잘못된 가정(wrong assumptions)으로 발생하는 error라고 생각할 수 있다. 예를 들어서 어떤 데이터에 대해서 linear regression model로 적용했을 때, 우리는 여기서 데이터가 'linear'한 특징이 있다고 가정을 한 것이다. 여기서 만약 데이터가 linear 하지 않고 굉장히 복잡한 형태라면, 잘못된 가정을 한것이다.

Bias : amount of assumptions your model has.

$Y$를 우리가 알고싶어 하는 true value of parameter라고 하고, $\hat{Y}$을 sample data로부터 추정한 $Y$라고 하면, 추정량 $\hat{Y}$의 bias는 다음과 같이 주어진다.

위 식을 그림으로 표현하면 대략적으로 다음과 같이 표현할 수 있다.

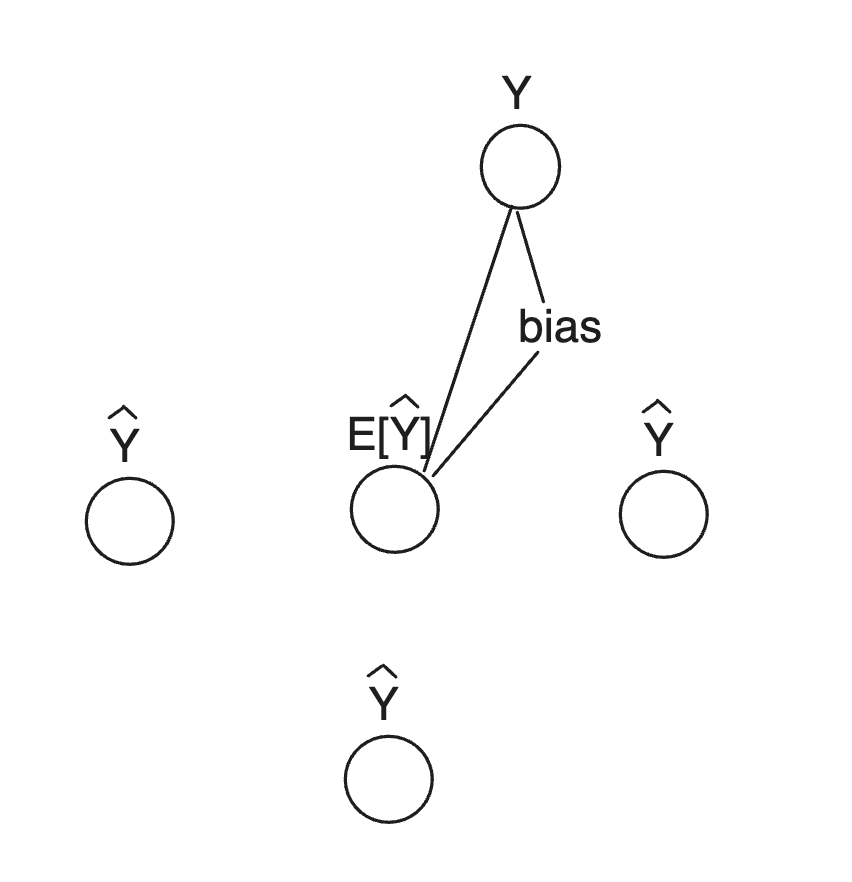
High-bias(more assumption)

bias 값이 크다는 것은 많은 가정이 들어갔음을 의미한다. 이러한 경우에는 모델은 training dataset에 제대로 fit했다고 볼 수 없다. 따라서 high-bias model은 dataset의 경향성을 제대로 포착하지 못하고, 이는 underfitting으로 여겨진다. 보통은 linear regression처럼 매우 단순한 알고리즘을 modeling에 사용했기 때문에 발생한다.(단순한 알고리즘의 모델링은 데이터셋에 많은 가정이 들어간 것이기 때문)

Low Bias(fewer assumption)

bias가 작다는 것은 적은 가정이 들어갔음을 의미한다. 이런 경우에는 model은 training dataset에 잘 fit한다.

Biased estimator & Unbiased estimator

대표적으로 모평균을 추정할 때, 표본평균을 사용하는 것이 표본 평균의 모평균의 unbaised estimator이기 때문이라는 개념을 포함해서 통계를 공부하다보면 biased estimation unbiased estimation에 대해서 한 번쯤은 들어봤을 것이다.

각각에 대해서 알아보면,
Unbiased estimator는 파라미터의 추정량의 평균에 대해서 bias값이 0인 경우를 말하고 biased estimator는 bias값이 0이 아닌 경우를 말한다.

즉,파라미터를 $\theta$ estimator를 $\hat{\theta}$라 하면, 위에서 살펴본 bias가 0이어야 하므로 식으로 나타내면 다음과 같다.
$Bias(\theta) = E(\hat{\theta}) - \theta = 0$이므로 $E(\hat{\theta}) = \theta$ 이면 추정량 $\hat{\theta}$을 $\theta$의 unbiased estimator라고 한다.

예를들어서 모평균 $\mu$에 대해서 추정량 $\hat{\theta}$을 다음과 같이 정의했을 때, $\hat{\theta} = \frac{X_1+X_2+X_3}{3}$

따라서 $\hat{\theta}$은 모수 $\theta$에 대해서 unbiased estimator이다.

Unbiased가 무조건 좋은가?

unbiased estimator인 경우에 앞서 언급했듯이 추정량의 평균이 모수와 일치함을 의미한다. 따라서 추정량으로 unbiased 성질을 갖고 있는 것 이를 '불편성'이라고 하는데, 우리가 추정량이 갖추었으면 하는 바람직한 성질들 중 불편성을 만족하는지 확인하는 이유이다.

불편성을 만족하기 위해서 모분산 $\sigma^2$에 대한 추정량 $S^2 = \frac{\sum_{i=1}^n(X_i-\bar{X})^2}{n-1}$ 여기서 분모에 n이 아닌 n-1이 들어간다.

그렇다면 unbiased estimator가 무조건 좋은가에 대한 궁금증이 생긴다.
답부터 이야기하자면, 무조건 좋다고 판단할 수 없다. 왜냐하면 결국 추정량의 평균이기 때문인데, 만약 우리가 추정한 파라미터가 (1, -1, 1, -1)이 나온 것과 (100, -100, 100, -100)이 나온게 있다고 하면, 이 둘의 Bias는 0으로 같지만, 각각의 추정치들끼리의 변화량이 매우 크기 때문에, bias가 낮다고 무조건 좋다고 말할 수 없다.

Variance

Variance는 data의 평균에서 얼마나 퍼져있는지를 나타내는 척도인데, model 관점 또는 machine learning 관점에서 variance는 training dataset의 다른 하위집합을 모델이 만났을 때, 얼마나 민감한지에 대한 것을 나타낸다.
$Y$를 target 변수의 실제 값이라 하고, $\hat{Y}$를 target 변수의 예측값이라 하면, model의 variance는 실제값과 예측값의 차이의 제곱의 기댓값으로 표현할 수 있다.
$Variance = E[(\hat{Y}-E[\hat{Y}])^2]$

Variance : Sensitivity of the model to the training data.

Low variance

low variance는 model이 일반화 능력이 좋다고 볼 수 있다.

high variance

high variance는 모델이 매우 민감하기 때문에, training data의 변화는 결과에 큰 변화를 줄 수 있다.

Bias와 Variance

지금까지 Bias와 Variance에 대해서 알아봤는데, model 입장에서 결국 loss이기 때문에 둘다 작게 만드는 것이 좋다. bias와 분산에서 가장 유명한 그림을 보면 4가지 경우로 분류하여 설명한다.

• 1. Low Bias, Low Variance : 추정값들이 모수와 가깝고 서로 모여 있음.
• 2. Low Bias, High Variance : 추정값들이 모수와 가깝고, 서로 떨어져 있음.
• 3. High Bias, Low Variance : 추정값들이 모수와 멀고, 서로 모여 있음.
• 4. High Bias, High Variance : 추정값들이 모수와 멀고, 서로 떨어져 있음.

Bias와 Variance의 Trade-Off 관계

만약 우리가 복잡한 데이터를 가지고 회귀 모델을 고려한다면, 1차 회귀 모델로는 데이터를 완벽하게 설명할 수 없기 때문에 high bias(실제 데이터와 모델의 예측값의 차이가 큼)를 가질 것이다. 하지만, 이 모델은 간단하기 때문에, training data에 대한 변동성이 낮을 것이다. 따라서 low variance를 가진다.
bias를 낮추기 위해서 고차원의 선형 회귀 모델을 고려하면, low bias가 되겠지만, 데이터에 overfitting되기 쉽다. 따라서 새로운 data에 대해서 높은 변동성을 보이고 이는 high variance를 가진다.
따라서 bias와 variance는 서로 trade-off 관계에 있다.

bias를 줄이면 vriance가 증가하고, vriance를 줄이면 bias가 증가한다.

MSE(Mean Square Error)

MSE는 model의 total loss를 측정하는 지표이다. MSE는 다음과 같은 수식으로 나타낸다.
$MSE = E[(y-\hat{y})^2]$ 즉 오차제곱의 평균이다.

Random Variable X에 대해서 $Var(X) = E(X^2) - E(X)^2$ 이고 $E(X^2) = Var(X) + E(X)^2$이다.

$MSE = E[(y-\hat{y})^2] =Var(y-\hat{y})+E[y-\hat{y}]^2$
$=Var(\hat{y}) + (y-E(\hat{y}))^2$
이는 결국
$=Variance(\hat{y}) + Bias^2(\hat{y})$ 으로 나타낼 수 있다.

즉 Bias와 Variance의 Trade-off 관계로 인해서 MSE에는 Variance와 Bias를 적절하게 조율할 수 있도록 두 개의 텀이 들어가 있다.

참고

https://gaussian37.github.io/machine-learning-concept-bias_and_variance/
https://for-my-wealthy-life.tistory.com/31
https://en.wikipedia.org/wiki/Mean_squared_error
https://youtu.be/nbY2KqXSsaE