통계학

중심극한정리는 많은 확률변수들의 합이 근사적으로 정규분포를 따르는 조건을 결정하는 것과 관련이 있다.중심극한정리는 독립인 확률변수들의 합에 대한 근사적인 확률을 계산하는 간단한 방법을 제공할 뿐만 아니라 대부분의 모집단의 경헙적 도수분포표들이 종모양(즉, 정규) 곡선을

$X = X(\\omega)$가 표본공간 $\\Omega$ 위에서 정의된 실수치 함수일 때, 임의의 실수 $x$에 대하여 사상 ${X \\leq x}$가 확률사상이면, $X$를 확률변수(random variable)라 한다. (확률이 정의되는 사상을 확률사상이라 한다.

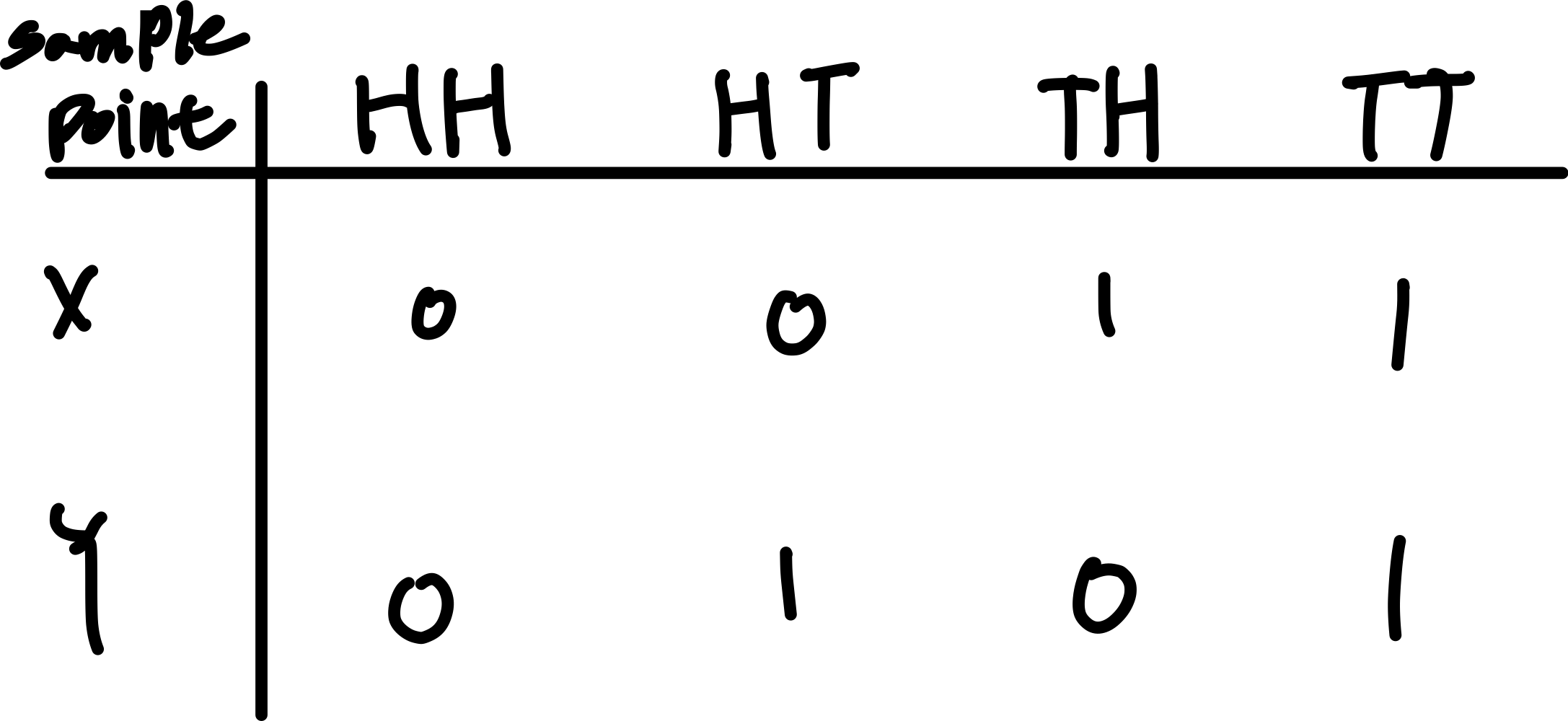
지난 포스트에서 확률 변수와 확률 분포에 대해서 다루었다. 지난번까지 공부한 내용에서는 하나의 표본 공간에 하나의 확률 변수를 정의한 경우를 살펴봤었는데, 이번 포스트에서는 하나의 표본공간에 대해서 1개 이상의 확률변수를 정의한 경우에 대해서 공부하려고 한다. 예를 들

지난 포스팅에서는 결합확률분포와 주변확률분포에 대해서 알아봤다. 포스팅참고이번 포스팅에서는 확률변수가 이산확률변수일 때와 연속확률변수일 때 조건부확률함수와 조건부밀도함수에 대해서 알아보려고 한다. 사상 A가 주어진 조건에서 사상 B의 조건부확률 $P(B|A)$는$$P(

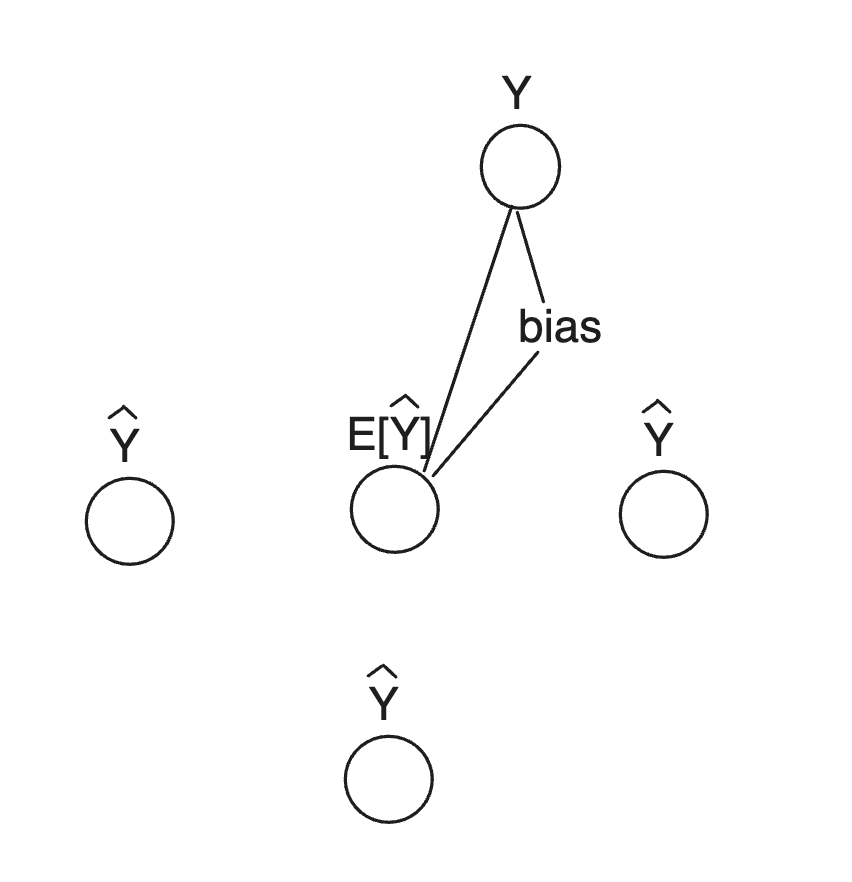
이번 포스팅에서는 통계학에서 자주 등장하지만 헷갈리는 용어들을 정리하고 알아보려고 한다. 통계학이나 머신러닝을 공부하다보면, bias, variance, residual, error 등의 용어들을 많이 접할 수 있다. 모두 비슷한 것처럼 알고 있지만 모두 다른 의미를