미분이 뭔가요?
변수의 움직임에 따른 함수값의 변화를 측정하기 위한 도구로 최적화에서 제일 많이 사용하는 기법
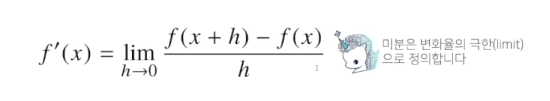

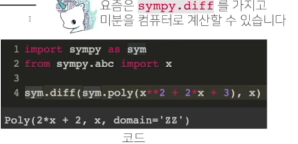
- 최근엔 미분을 손으로 직접 계산하는 대신 컴퓨터가 계산해 줄 수 있습니다.
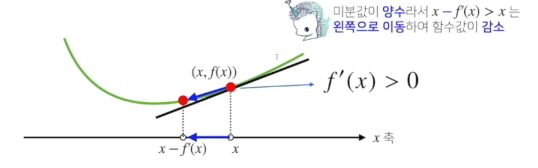
- 미분은 함수f의 주어진 점(x, f(x))에서의 접선의 기울기를 구한다.
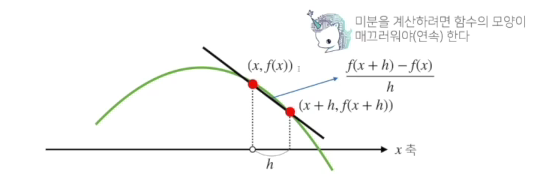
- 한 점에서 접선의 기울기를 알면 어느 방향으로 점을 움직여야 함수 값이 증가하는지/ 감소하는지 알수 있다
- 증가사키고 싶다면 미분값을 더하고, 감소시키고 싶으면 미분값을 뺍니다.
- 증가
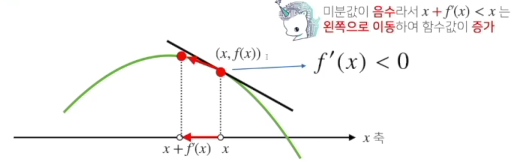
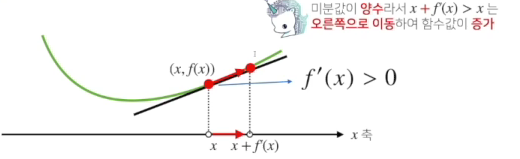
- 감소
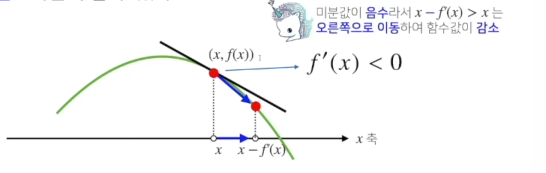
- 증가
- 증가사키고 싶다면 미분값을 더하고, 감소시키고 싶으면 미분값을 뺍니다.
- 미분값을 더하면 경사상승법이라하며 함수의 극대값의 위치를 구할 때 사용한다.
- 미분값을 빼면 경사하강법이라 하며 함수의 극소값의 위치를 구할때 사용한다.
- 극값에 도달하면 움직임을 멈춘다.
- 극값에서 미분값이 0이므로 더 이상 업데이트가 안된다. 그러므로 목적함수 최적화가 자동으로 끝난다.
경사하강법의 알고리즘

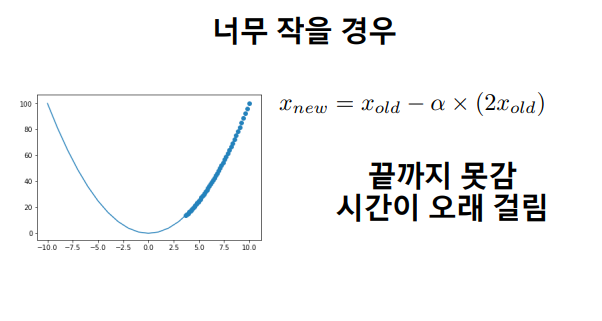
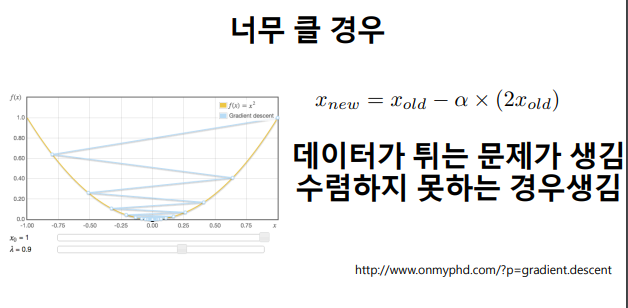
- 학습률은 조심스럽게 조정하여야 함
변수가 벡터이면요?
- 미분은 변수의 움직임에 따른 함수값의 변화를 측정하기 위한 도구로 최적화에서 제일 많이 사용하는 기법입니다.
- 벡터가 입력인 다변수 함수의 경우 편미분을 사용한다

- 각 변수별로 편미분을 계산한 그레디언트 벡터를 이용하여 경사하강/경사상승법에 사용할 수 있다.
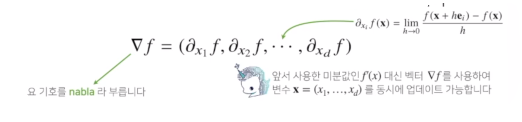
그레디언트 벡터
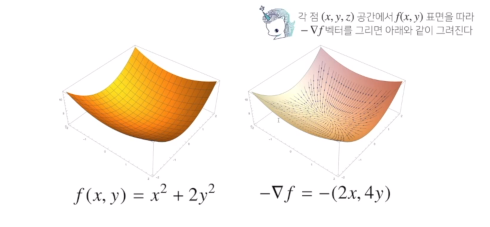
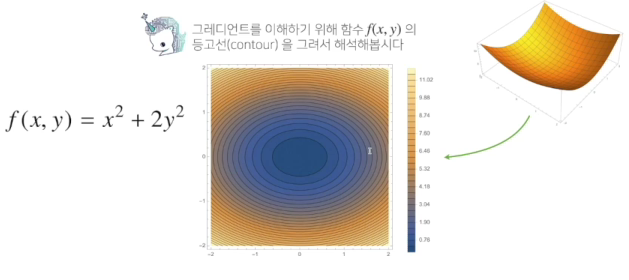
- 가장 빨리 증가하는 방향
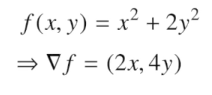
- 가장 빨리 감소하게 되는 방향
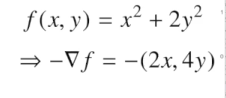

[참고]
1.Andrew Ng 강의
경사하강법
- 비용함수가 전체 데이터셋의 예측이 얼마나 잘 평가되었는지 보는 것이라면, 경사하강법은 이를 가능케하는 파라미터 w와 b를 찾아내는 방법 중 하나 입니다.
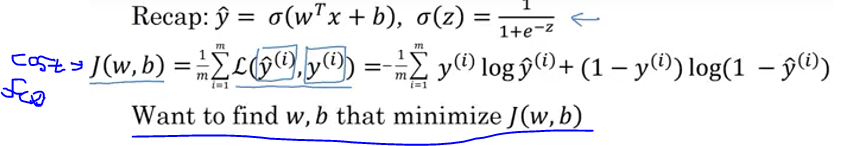
- 우선, 비용 함수는 볼록한 형태여야 합니다. 볼록하지 않은 함수를 쓰게 되면, 경사하강법을 통해 최적의 파라미터를 찾을 수 없습니다.

- 함수의 최소값을 모르기 때문에, 임의의 점을 골라서 시작합니다.
- 경사하강법은 가장 가파른(steepest) 방향, 즉 함수의 기울기를 따라서 최적의 값으로 한 스텝씩 업데이트하게 됩니다.
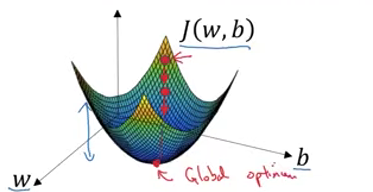

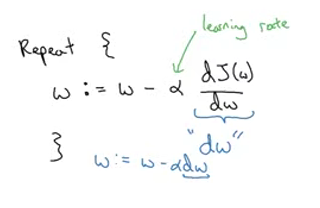
- 만약 dw >0 이면, 파라미터 w 는 기존의 w 값 보다 작은 방향으로 업데이트 될 것이고, 만약 dw <0 이면, 파라미터 w 는 기본의 w 값 보다 큰 방향으로 업데이트 될 것입니다.
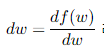

로지스틱 회귀의 경사하강법
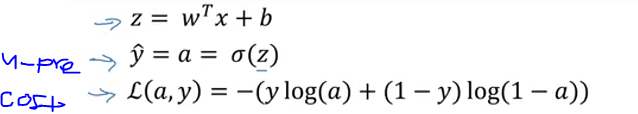
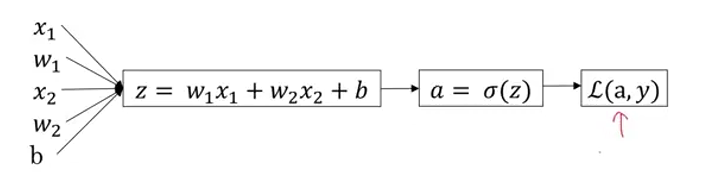
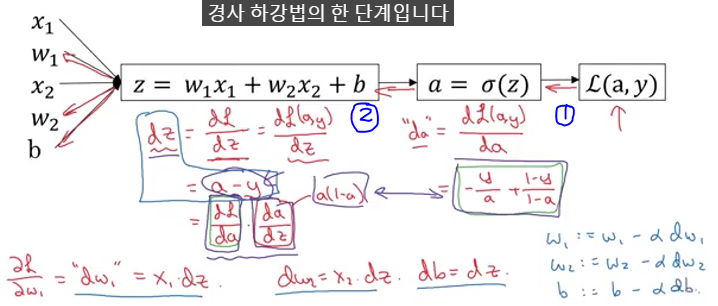
m개 샘플의 경사하강법
- 로지스틱 회귀에서 비용 함수
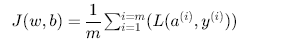

- 특성의 개수를 2개로 가정하였지만, 만약 특성의 개수가 많아진다면 이 또한 for문을 이용해 처리해야 합니다. 즉, 이중 for문을 사용하게 되며 이로인해 계산속도가 느려지게 됩니다.
- ectorization을 통해 for문을 사용하지 않고 처리할 수 있는 방법 있음
신경망 네트워크와 경사 하강법


- 파이토치로 시작하는 딥러닝
Linear regression
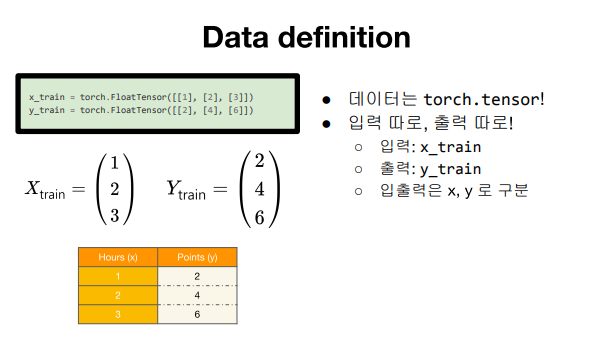




3.머신러닝을 위한 파이썬
Linear Regression - Gradient Descent
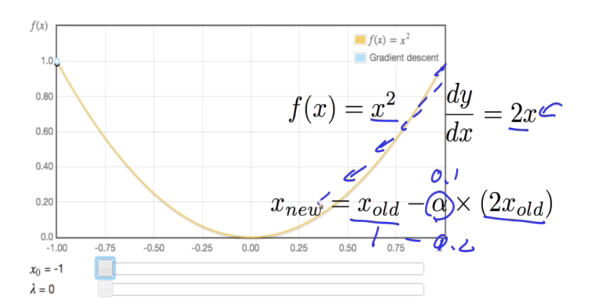
- 정해야할것 : learning rate, 얼마나 많이 loop을 돌것인가?