Warm-up
선형회귀분석 기초
Tabular Data
tabular data 는 쉽게 생각해 데이터프레임
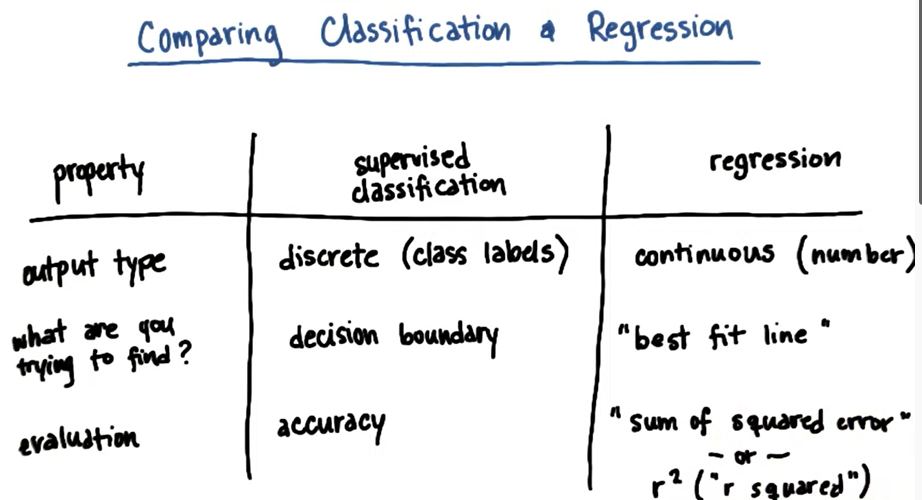
classification vs Regression
선형회귀분석
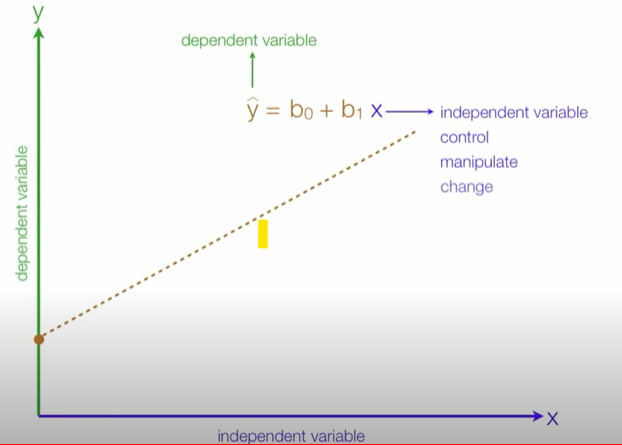
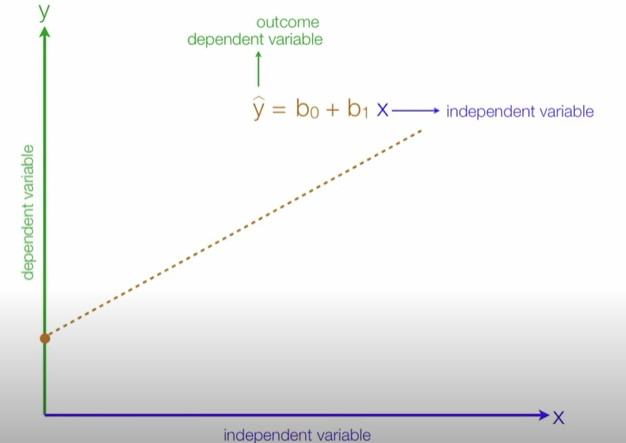
주어진 독립변수와 종속변수간의 관계를 파악하여 그 관계를 가장 잘 설명(best-fit)할수 있는 회귀선(Regression line,best-fit-line)찾고 이 선을 통해 새로운 input변수를 기반으로 output변수를 예측
- 종속변수의 개수는 언제나 한개, 단순선형회귀분석은 독립변수가 한개, 다중선형회귀분석은 독립변수가 두개 이상
이미지 출처
기준모델
예측 모델을 구체적으로 만들기 전에 가장 간단하면서도 직관적이면서 최소한의 성능을 나타내는 기준이 되는 모델
- 분류문제: 타겟의 최빈 클래스
- 회귀문제: 타겟의 평균값
- 시계열회귀문제: 이전 타임스탬프의 값
predict = df['Price'].mean() #평균을 기준모델로
Mean Absolute Error(MAE, 평균절대오차)
MAE정리errors = predict - df['SalePrice'] mean_absolute_error = errors.abs().mean()
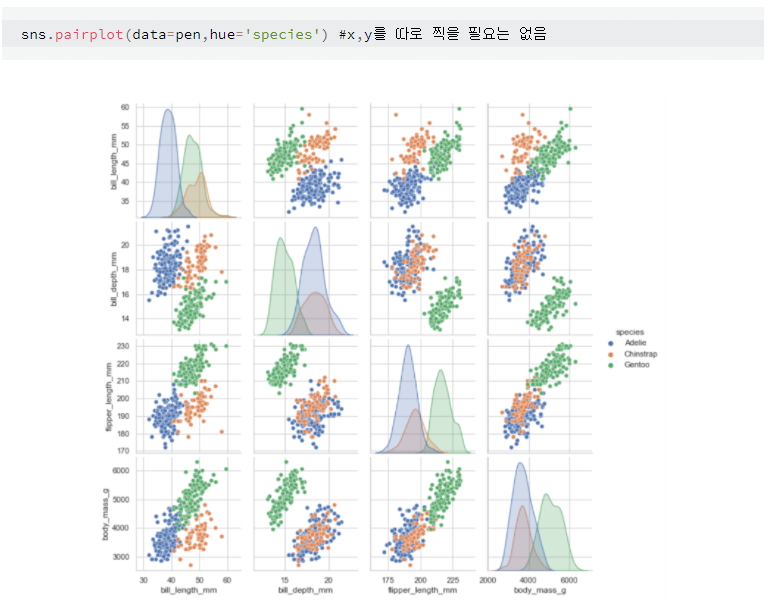
pairpolt
주어진 데이터의 각 feature들 사이의 관계를 표시하는 Plot. 출처
예측모델
훈련 vs 테스트
모든 데이터를 기계에게 학습시켜서는 안 됌
테스트용으로 데이터 중 일부는 남겨 두고 훈련용 데이터만 훈련에 사용
why? 그래야만 기계가 학습을 하고나서,현재 성능이 얼마나 되는지를 측정할수 있으며 과적합을 막을수 있습니다
- 검증용 데이터:검증용 데이터는 현재 모델의 성능, 기계가 훈련용 데이터로 얼마나 제대로 학습이 되었는지를 판단하는 용으로 사용되며 검증용 데이터를 사용하여 모델의 성능을 개선하는데 사용(모의고사)
- 테스트용 데이터: 모델의 최종 성능을 평가하는 데이터로 모델의 성능을 개선하는 일에 사용되는 것이 아니라, 모델의 성능을 수치화하여 평가하기위해 사용(수능)
출처데이터셋 분리하기
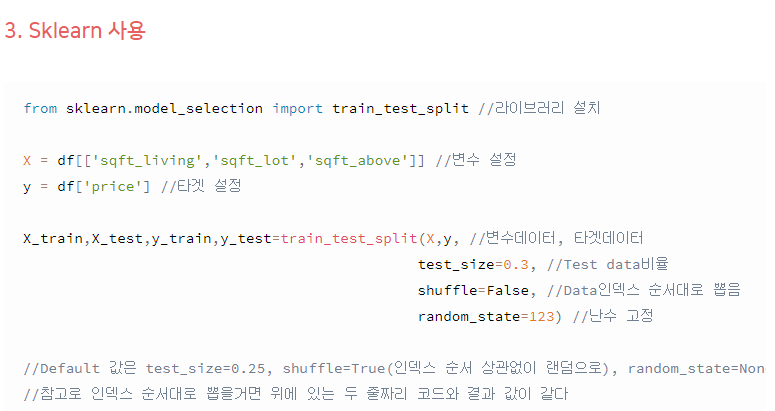
위 링크에서 SKlearn 사용하는 법
sklearn.model_selection.train_test_split (train/test = 80%/20%)
from sklearn.model_selection import train_test_split X=df.drop(columns='Price') #'price'를 제외한 df를 특성으로 지정 y=df['Price'] X_train, X_test, y_train, y_test = train_test_split(X,y, test_size=0.2, random_state=2)
용어
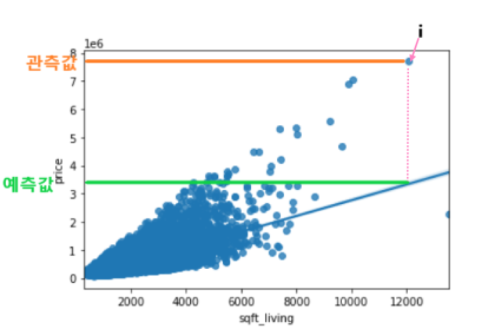
- 예측값: 만들어진 모델이 추정하는 값
- 잔차: 예측값과 관측값 차이
- 오차(error): 모집단에서의 예측값과 관측값 차이
- RSS(residual sum of squares): 잔차 제곱들의 합= SSE(Sum of Square Error)
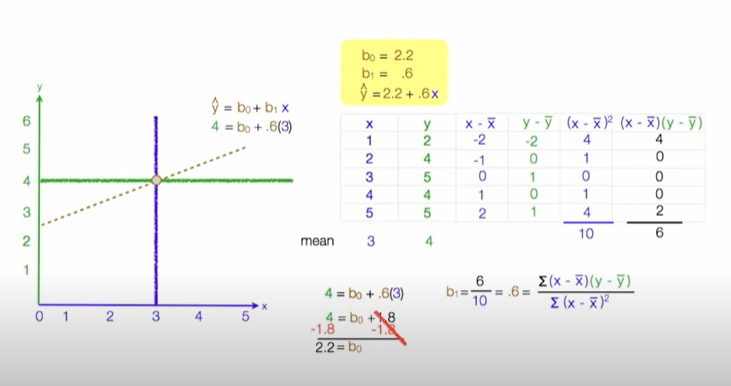
는 회귀계수, 는 y의 절편
계수 와 는 RSS를 최소화 하는 값으로 모델 학습을 통해서 얻어지는 값
- 비용함수: RSS를 함수로 표현한 것
- 회귀선:RSS를 최소화 하는 직선
- 학습(in 머신러닝): 비용함수를 최소화 하는 모델을 찾는 과정
- Ordinary least squares(OLS): 잔차제곱합을 최소화하는 방법
- 선형회귀는 주어져 있지 않은 점의 함수값을 보간(interpolate) 하여 예측하는데 도움
- 선형회귀모델은 기존 데이터의 범위를 넘어서는 값을 예측하기 위한 외삽(extrapolate)도 제공
선형회귀 직선은 독립변수(independent variable, x)와 종속변수(dependent variable, y) 간의 관계를 요약해 줍니다.
- 종속변수는 반응(Response)변수, 레이블(Label), 타겟(Target)등
- 독립변수는 예측(Predictor)변수, 설명(Explanatory), 특성(feature) 등
seborn으로 regplot 그리기
improt seaborn as sns sns.regplot(x=df['GrLivArea'], y=df['SalePrice']);
scikit-learn을 사용해서 선형회귀모델
기본 데이터 구조

- 특성 데이터와 타겟 데이터를 나눔
- 특성행렬은 주로 X 로 표현하고 보통 2-차원 행렬
([n_samples, n_features]). 주로 NumPy 행령이나 Pandas 데이터프레임으로 표현합니다.
-타겟배열은 주로 y로 표현하고 보통 1타원 형태(n_samples) 입니다. 주로 Numpy 배열이나 Pandas Series로 표현합니다.모델구현 프로세스
우선 풀어야 하는 문제를 풀기에 적합한 모델을 선택하여 클래스를 찾아본 후 관련 속성이나 하이퍼파라미터를 확인해 봅니다.
문제에 따라서 약간 차이가 있겠지만 위에서 살펴본 것과 같이 데이터를 준비
fit() 메소드를 사용하여 모델을 학습
'predict()' 메소드를 사용하여 새로운 데이터를 예측
1) 모델 정의 : model = LineRegression()
2) 데이터 학습 : model.fit(x,y)
3) 모델 적용 : model.predict(new 변수)##Scikit-Learn 라이브러리에서 사용할 예측모델 클래스를 Import 합니다from sklearn.linear_model import LinearRegression ## 예측모델 인스턴스를 만듭니다 model = LinearRegression()## X 특성들의 테이블과, y 타겟 벡터를 만듭니다 feature = ['GrLivArea'] target = ['SalePrice'] X_train = df[feature] y_train = df[target]## 모델을 학습(fit)합니다 model.fit(X_train, y_train)#새로운 데이터 한 샘플을 선택해 학습한 모델을 통해 예측 pred= model.predict([[50]])model.coef_ #계수 --------------- array([[107.13035897]]) #107이라는 수치 크기가 한 유닛 커질수록 가격이 107달러 오른다는 것을 알 수 있음## 절편(intercept) model.intercept_예측 함수 만들기
def explain_prediction(sqft): y_pred = model.predict([[sqft]]) pred = f"{int(sqft)} sqft 주택 가격 예측: ${int(y_pred[0])} (1 sqft당 추가금: ${int(model.coef_[0])})" return predipywidgets 사용
from ipywidgets import interact # 데코레이터 interact를 추가합니다. @interact def explain_prediction(sqft=(500,10000)): y_pred = model.predict([[sqft]]) pred = f"{int(sqft)} sqft 주택 가격 예측: ${int(y_pred[0])} (1 sqft당 추가금: ${int(model.coef_[0])})" return pred