Warm-up

훈련/테스트 데이터

Train VS Test

• 모델의 성능을 평가하기 위해 훈련/테스트 데이터로 나눔
• 모델 학습에 사용한 훈련(train) 데이터를 잘 맞추는 모델이 아니라, 학습에 사용하지 않은 테스트(test) 데이터를 얼마나 잘 맞추는지
• 데이터를 훈련/테스트 데이터로 나누어야 우리가 만든 모델의 예측 성능을 제대로 평가
• 데이터 나누는 방법:
  1.데이터를 무작위로 선택해 나누는 방법이 일반적
  2.시계열 데이터를 가지고 과거에서 미래를 예측하려고 하는 경우 이때는 훈련 데이터 보다 테스트 데이터가 미래의 것
  (주의: 시간 데이터가 있다고 해서 항상 시계열 데이터는 아님)

Validation VS Test
1.검증 데이터 (validation data): 모델 검증용 데이터

• 한 모델 안에서 최적의 하이퍼파라미터(사용자가 임의로 지정해야 하는 파라미터)를 찾아주는 데이터
• 선형회귀모델 같은 경우 하이퍼파라미터가 존재하지 않고 유일하게 존재하는 간단한 모델이라 검증 데이터를 쓸 필요가 없음
• but, 추후에 배우는 복잡한 모델에서는 Train data를 다시 분리하거나 미리 나눠 검증 데이터를 만든 후 검증 데이터에 대한 성능을 통해 하이퍼파라미터를 조정하는 과정을 거침

2. 테스트 데이터 (test data): 한번 딱 검정하는 것

• 다른 모델끼리의 성능을 평가하는 데이터
• 어떤 모델이 더 좋은 지에 대해 모델 마다 같은 test data를 적용하여 성능을 비교하는 것입니다.

검증 데이터: 반 1등(같은 모델안에서)을 뽑는데 쓰이는 데이터
테스트 데이터:전교 1등(여러 다른 모델 간)을 뽑는데 쓰이는 데이터

무작위로 나누기

## 데이터의 75% 갯수
len(df)*0.75

train = df.sample(frac=0.75,random_state=1)
test = df.drop(train.index)

시계열 데이터 나누기

test = df.loc[df.date>='2019-05-13']
train = df.loc[df.date<'2019-05-13'] #'2019-05-13'을 기준으로 나누기

참고

다중선형회귀모델 학습

기준모델

predict = y_train.mean() # 평균값으로 예측(기준모델)

# 기준모델로 훈련 에러(MAE) 계산
from sklearn.metrics import mean_absolute_error
y_pred = [predict] * len(y_train)
mae = mean_absolute_error(y_train, y_pred)

scikit-learn으로 다중선형회귀 모델

# 다중모델 학습을 위한 특성
features = ['feature1', 
            'feature2']
X_train = train[features]
X_test = test[features]

# 모델 fit
model.fit(X_train, y_train)
y_pred = model.predict(X_train)
mae = mean_absolute_error(y_train, y_pred)
print(f'훈련 에러: {mae:.2f}')

# 모델 fit
model.fit(X_train, y_train)
y_pred = model.predict(X_train)
mae = mean_absolute_error(y_train, y_pred)
print(f'훈련 에러: {mae:.2f}')

하나의 특성을 사용한 단순선형회귀모델보다 테스트 오류가 더 줄어듬

회귀계수

• 단순선형회귀식: $y= \beta_0 + \beta_1 x$
• 2특성의 다중선형회귀 식: $y = \beta_0 + \beta_1x_1 + \beta_2x_2$

model.intercept_, model.coef_
---------------------------
(-102743.02342270731, array([54.40145532, 33059.44199506]))

#회귀식
b0 = model.intercept_
b1, b2 = model.coef_
print(f'y = {b0:.0f} + {b1:.0f}x\u2081 + {b2:.0f}x\u2082')
---------------------------------------------
y = -102743 + 54x₁ + 33059x₂

• x2 계수가 더 크니까 더 y 값에 영향을 더 많이 줌
• $\beta_1$과 $\beta_2$ 모두 양수이므로 $x_1$, $x_2$이 증가할 때마다 $y$ 도 증가한다

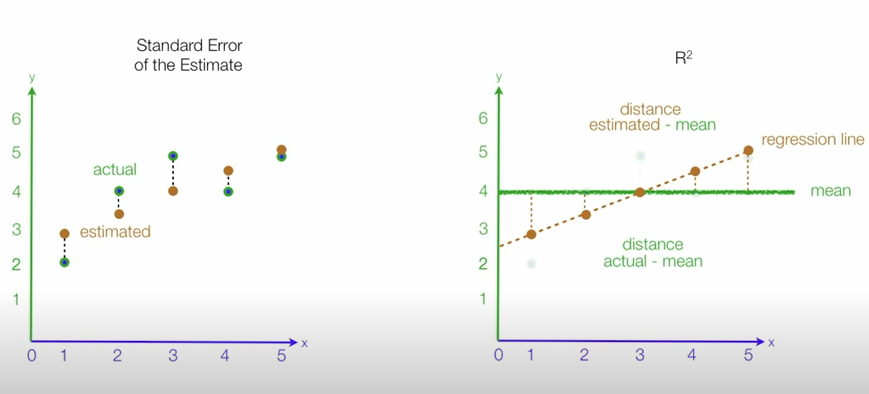
평가지표(evaluation metric)

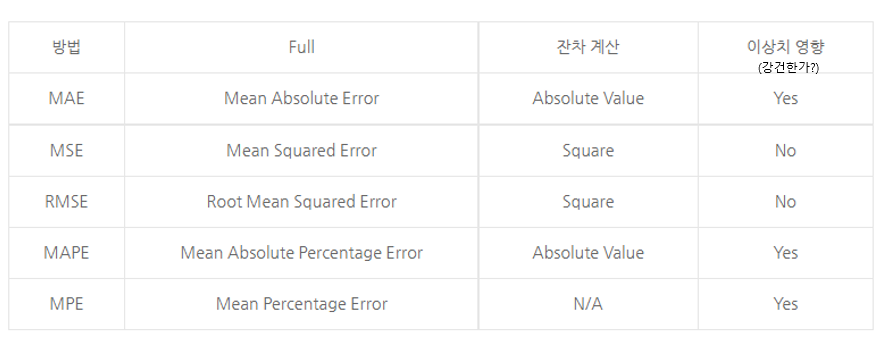
1. MSE (Mean Squared Error) = $\frac{1}{n}\sum_{i=1}^{n}(y_{i} - \hat{y_{i}})^{2}$

from sklearn.metrics import mean_absolute_error
mean_absolute_error(y_test, y_pred)

• 예측값과 실제값 차이의 면적의 합
• 특이값이 존재하면 수치가 많이 늘어난다.
• 제곱을 하기때문에 단위가 변해서 오류를 확인할때 어느정도 오류인지 확인어려움, 너무 큰 변수 같은 이상치에 매우 민감하다는 단점

2. MAE (Mean absolute error) = $\frac{1}{n}\sum_{i=1}^{n}\left | y_{i} - \hat{y_{i}} \right |$

from sklearn.metrics import mean_squared_error 
mean_squared_error(y_test, y_pred)

• MAE는 에러에 절대값을 취하기 때문에 에러의 크기 그대로 반영된다. 그러므로 예측 결과물의 에러가 10이 나온 것이 5로 나온 것보다 2배가 나쁜 도메인에서 쓰기 적합한 산식이다.
• 에러에 따른 손실이 선형적으로 올라갈 때 적합하다.
• 이상치가 많을 때
• 오류가 나왔을때 직관적으로 확인할수 있음

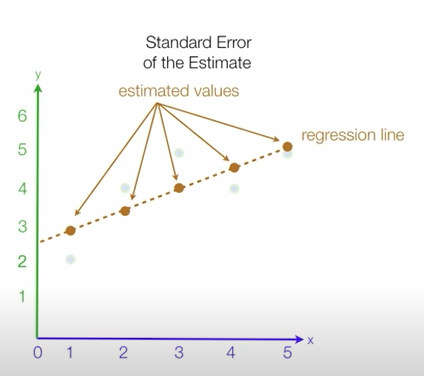
3. RMSE (Root Mean Squared Error) = $\sqrt{MSE}$

from sklearn.metrics import mean_squared_error 
MSE = mean_squared_error(y_test, y_pred) 
np.sqrt(MSE)

• MSE 값은 오류의 제곱을 구하므로 실제 오류 평균보다 더 커지는 특성이 있어 MSE에 루트를 씌운 RMSE 값을 쓴다.
• 에러에 제곱을 하기 때문에 에러가 크면 클수록 그에 따른 가중치가 높이 반영된다. 그러므로 예측 결과물의 에러가 10이 나온 것이 5로 나온 것보다, 정확히 2^2(4)배가 나쁜 도메인에서 쓰기 적합한 산식이다.
• 에러에 따른 손실이 기하 급수적으로 올라가는 상황에서 쓰기 적합하다.
• 이창치에서 많이 활용

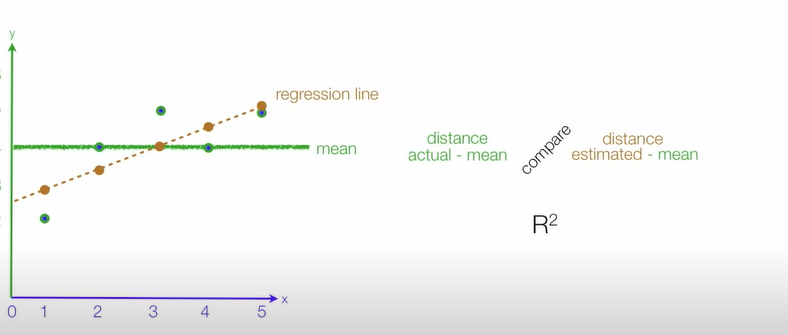
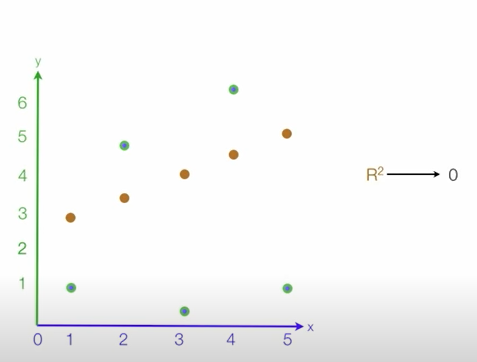
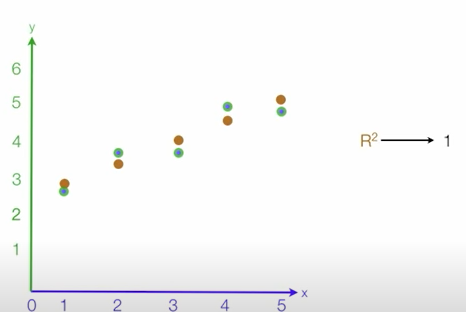
4. R-squared (Coefficient of determination: 결정계수) =
   $1 - \frac{\sum_{i=1}^{n}(y_{i} - \hat{y_{i}})^{2}}{\sum_{i=1}^{n}(y_{i} - \bar{y_{i}})^{2}} = 1 - \frac{SSE}{SST} = \frac {SSR}{SST}$

rom sklearn.metrics import r2_score
r2 = r2_score(y_train, y_pred)

• 다른 지표들과 달리 scale영향을 받지 않아 상대적으로 성능이 어느정도 판단할 수 있음
• 회귀모델의 설명력을 표현(0~1) 1에 가까울수록 모델이 데이터에 대한 설명력이 높다라고 설명가능
  
  출처

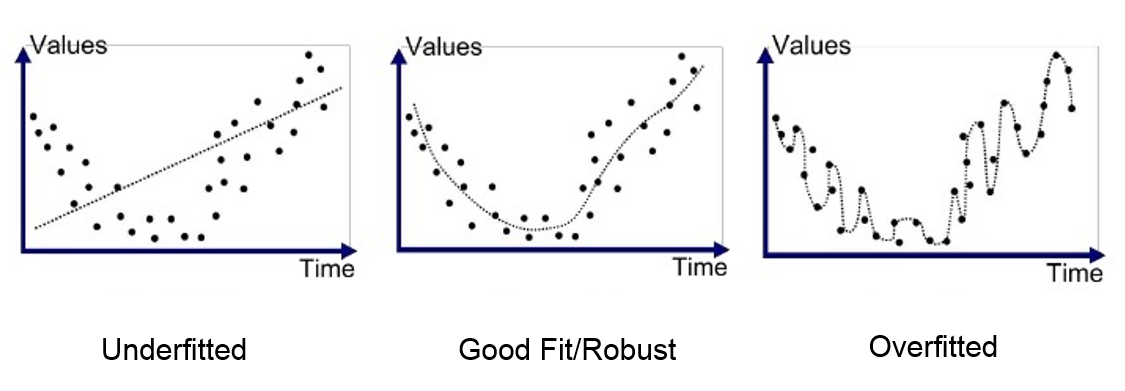
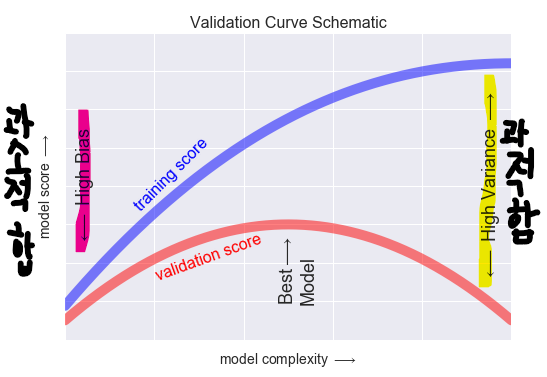
과접합 VS 과소접합

1. 훈련데이터에서와같이 테스트데이터에서도 좋은 성능을 내는 모델은 일반화가 잘 된 모델
2. 과적합(Overfitting): 모델이 훈련데이터에만 특수한 성질(노이즈)을 과하게 학습해 일반화를 못해 결국 테스트데이터에서 오차가 커지는 현상
3. 과소적합(Underfitting): 훈련데이터에 과적합도 못하고 일반화 성질도 학습하지 못해, 훈련/테스트 데이터 모두에서 오차가 크게 나오는 경우를 말합니다. -너무 간단해서 나타나는 문제

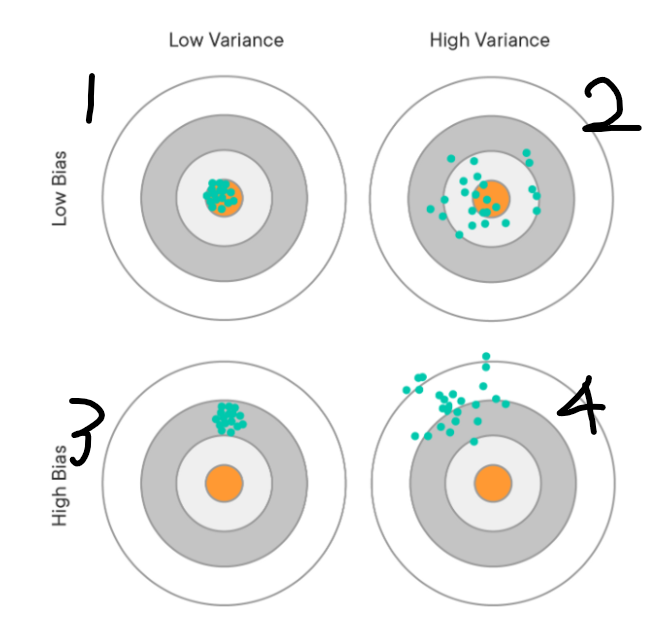
• 분산이 높은경우는, 모델이 학습 데이터의 노이즈에 민감하게 적합하여 테스트데이터에서 일반화를 잘 못하는 경우 즉 과적합 상태입니다.
• 편향이 높은경우는, 모델이 학습 데이터에서, 특성과 타겟 변수의 관계를 잘 파악하지 못해 과소적합 상태입니다.
  
  
  1번같이 편향도 분산도 적은 모델이 바람직(지향점)
  2번처럼 분산은 높고 편향이 낮은 것:Overfitting
  3번처럼 편향이 높고 분산이 낮은 것:Underfitting
  4번처럼 편향도 분산도 높은것은 피해야하는 모델
  
• 모델이 복잡해질 수록 훈련데이터 성능은 계속 증가하는데 검증데이터 성능은 어느정도 증가하다가 증가세가 멈추고 오히려 낮아진다.
• 보통 이 시점을 과적합이 일어나는 시점으로 파악하고 더 복잡한 모델은 불필요함
  이미지출처
  이미지 출처

Plotly 설치

!pip install plotly chart_studio --upgrade