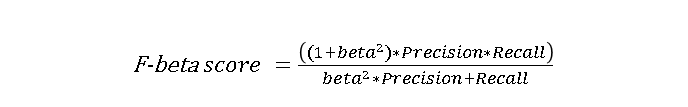DAY28

Warm-up

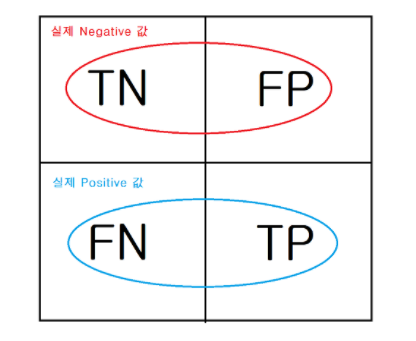
Confusion matrix

• TP: 예측(1)한 대로 실제로도 함(1)
• FP: 예측(1)을 했지만 실제로는 아님(0)
• TN: 예측(0)을 못했는데 실제로 안함(0)
• FN: 예측(0)을 못했는데 실제로 함(1)

Confusion matrix 시각화

from sklearn.metrics import plot_confusion_matrix
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
pcm = plot_confusion_matrix(pipe, X_val, y_val,                           cmap=plt.cm.Blues,
                            ax=ax, values_format = '');
plt.title(f'Confusion matrix, n = {len(y_val)}', fontsize=15)
plt.show()

이미지 출처

평가지표

• 정확도(Accuracy): 전체 범주를 모두 바르게 맞춘 경우를 전체 수로 나눈 값
  • 예측을 맞게 했는가?(직관적)
  • 이진 분류의 경우 데이터 구성에 따라 모델의 성능을 왜곡 할 수 있음
  • TN,TP에 좌우
  • 좋지 않은 예: 적은 수의 결과값에 postive(1)를 성정하고 그렇지 않는 경우(0)-암 진단, 보험 사기 등

$\large \frac{TP + TN}{Total}$

• 정밀도(Precision):Positive로 예측한 경우 중 올바르게 Positive를 맞춘 비율

  • FP를 낮추는 데 초점을 맞춤

  $\large \frac{TP}{TP + FP}$

from sklearn.metrics import recision_score
precision_score(y_test, pred)

• 재현율(Recall, Sensitivity): 실제 Positive인 것 중 올바르게 Positive를 맞춘 것의 비율

  • = TPR(True Positive Rate)
  • FN를 낮추는 데 초점을 맞춤

  $\large \frac{TP}{TP + FN}$

from sklearn.metrics import recall_score
recall_score(y_test, pred)

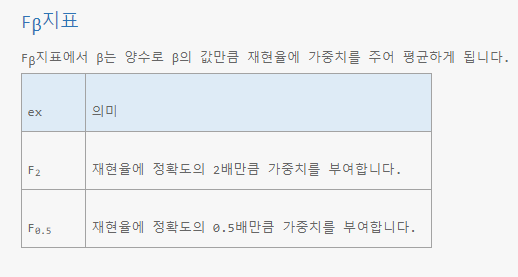
• F1점수(F1 score): 정밀도와 재현율의 조화평균(harmonic mean)
  (F 베타 스코어에서 베타가 1인 경우)

  • 정밀도와 재현율의 수치가 적절하게 조합돼 분류의 종합적인 성능 평가에 사용될 수 있는 평가 지표
  • 재현율와 정밀도 어느 한쪽으로 치우치지 않은 수치를 나타날때 F1 score은 상대적으로 높은 값을 가짐

  $2\cdot\large\frac{precision\cdot recall}{precision + recall}$

from sklearn.metrics import f1_score
f1 = f1_score(y_test, pred)

precision, recall, f1-score 한번에 보기

from sklearn.metrics import classification_report
print(classification_report(y_val, y_pred)) 

출처

정확도만으로 평가가 충분하지 않은 이유

데이터셋의 label값이 불균형(unbalance)한 경우엔 정확도는 좋은 측정을 할 수 없다

• 90명의 건강한사람과 10명의 환자가 있을 경우, 머신러닝이 모든 사람을 건강한 사람으로 예측할 경우에도 정확도는 90%가 된다. but, 환자 10명 모두가 건강하다고 분류됨

재현율 vs 정밀도

• 둘 다 Positive 데이터 세트의 예측 성능에 좀 더 초점을 맞춘 평가 지표
  • TP가 0이면 정밀도와 재현율 값이 모두 0이 된다.
  • 재현율과 정밀도 모두 TP를 높이는 데 동일한 초점
• Precision(정밀도)이 중요 지표인 경우
  : 실제 Negative 음성인 데이터 예측을 Positive 양성으로 잘못 판단하게 되면 업무상 큰 영향이 발생하는 경우
  • 예시)스펨메일 여부 판단하는 모델
• Recall(재현율)이더 중요 지표인 경우
  :실제 Positive 양성 데이터를 Negative로 잘못 판단하게 되면 업무상 큰 영향이 발생하는 경우
  • 초기 암 판단 모델, 보험 사기 적발 모델
• 가장 좋은 성능평가는 재현율과 정밀도 모두 높은 수치를 얻는 것이며, 반면에 둘 중 어느 한 평가 지표만 매우 높고, 다른 수치는 매우 낮으면 바람직 하지 않은 결과

정밀도&재현율 Trade-off

:둘의 상호 보완적인 특성 때문에 어느 한쪽을 강제로 높이면 다른 하나의 수치는 떨어지는 현상

• 정밀도 또는 재현율이 특별히 강조돼야 할 경우 분류의 결정 임곗값(Threshold)을 조정해 수치를 높일 수 있다
• 일반적으로 이진 분류에서는 임곗값을 0.5 (50%)로 정하고 임곗값보다 확률이 크면 Positive, 작으면 Negative로 결정
  • Randomforestclassifier 기본 임계값은 0.5
    출처

임계값(thresholds)

예측 확률 확인하기

• predict() : 예측 결과 클래스값
• predict_probba() : 예측 확률 결과

class 1인 확률 시각화

threshold = 0.5
y_pred_proba = pipe.predict_proba(X_val)[:, 1]
y_pred = y_pred_proba > threshold
ax = sns.histplot(y_pred_proba)
ax.axvline(threshold, color='red')
pd.Series(y_pred).value_counts()

해석
연두색부분은 0이 나올 확률, 분홍색 부분은 1이 나올 확률

임계값 조절해보기

from sklearn.preprocessing import Binarizer
thresholds = [0.5, 0.55, 0.60, 0.65, 0.70]
pred_proba = pipe.predict_proba(X_val)
def get_eval_by_threshold(y_val, pred_proba_c1, thresholds):
  for custom_threshold in thresholds:
    binarizer = Binarizer(threshold=custom_threshold).fit(pred_proba_c1)
    custom_predict = binarizer.transform(pred_proba_c1)
    print("\n임곗값 :", custom_threshold)
    get_clf_eval(y_val, custom_predict)

• 임계값이 낮을수록 정밀도는 낮아지고 재현율은 높아진다.
• 임계값이 높을수록 정밀도는 높아지고 재현율은 낮아진다

최적의 threshold 찾기

# threshold 최대값의 인덱스, np.argmax()
optimal_idx = np.argmax(tpr - fpr)
optimal_threshold = thresholds[optimal_idx]
print('idx:', optimal_idx, ', threshold:', optimal_threshold)

# 최적 임계치 적용하여 점수 확인
y_pred_optimal = y_pred_proba >= optimal_threshold
print(classification_report(y_val, y_pred_optimal))

출처

ROC 곡선과 AUC 점수

ROC 곡선

• 모든 임계값을 한눈에 보고 모델을 평가할 수 있는 방법, 머신러닝의 의 이진 분류 모델의 예측 성능을 판단하는 중요한 평가 지표이기도 함
  

1. FPR 이 변할 때, TPR 이 어떻게 변하는지를 나타내는 곡선
2. Roc 곡선이 가운데 직선에 가까울수록 성능이 떨어지는 것이며, 멀어질수록 성능이 뛰어난 것
3. 임곗값이 1이면 FP가 0이 되기 때문에 FPR은 0
4. 임곗값이 0이면 TN이 0이 되기 때문에 FPR은 1
5. 임계값을 1부터 0까지 변화시켜 FPR을 구한 후, FPR 값 변화에 따른 TPR 구하는 것이 ROC곡선
   

• 재현율을 높이기 위해서는 Positive로 판단하는 임계값을 계속 낮추어 모두 Positive로 판단하게 만들면 됨. but, 이렇게 하면 동시에 Negative이지만 Positive로 판단하는 위양성률도 같이 높아집니다.
• 재현율은 최대화 하고 위양성률은 최소화 하는 임계값이 최적의 임계값입니다.
• ROC curve는 다중분류문제에서 각 클래스를 이진클래스 분류문제로 변환(One Vs All)하여 구할 수 있습니다.
  • 3-class(A, B, C) 문제 -> A vs (B,C), B vs (A,C), C vs (A,B) 로 나누어 수행

from sklearn.metrics import roc_curve
# roc_curve(타겟값, prob of 1)
fpr, tpr, thresholds = roc_curve(y_val, y_pred_proba)
roc = pd.DataFrame({
    'FPR(Fall-out)': fpr, 
    'TPRate(Recall)': tpr, 
    'Threshold': thresholds
})
roc

plt.scatter(fpr, tpr)
plt.title('ROC curve')
plt.xlabel('FPR(Fall-out)')
plt.ylabel('TPR(Recall)');

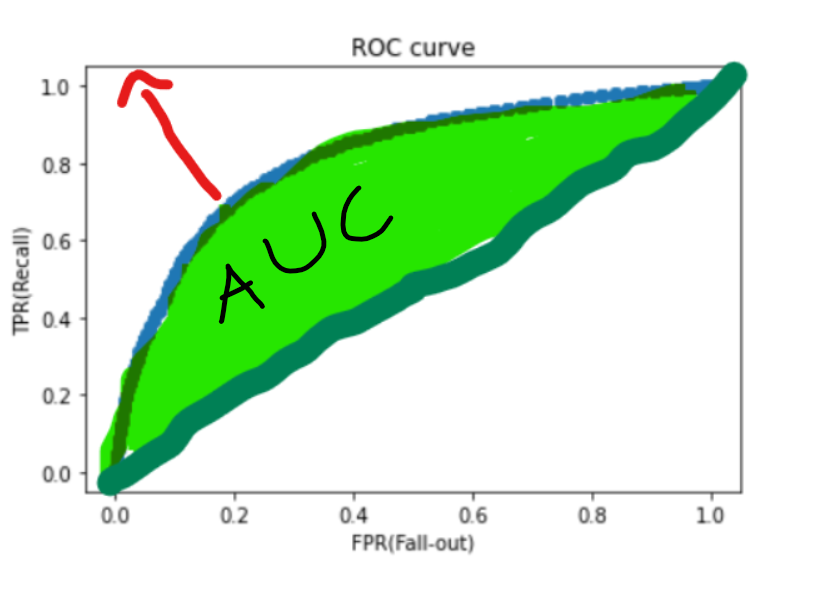
AUC 곡선

: ROC curve의 아래 면적

• 1에 가까울 수록 좋은 수치
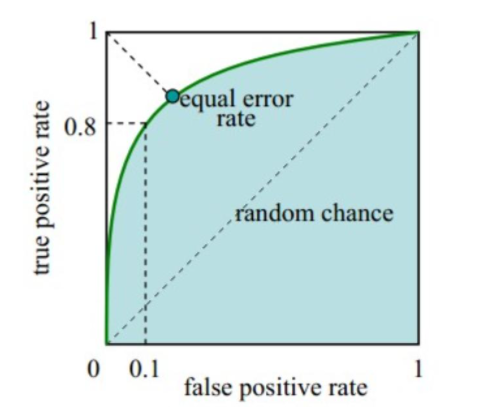
• AUC 수치가 커지려면 FPR이 작은 상태에서 얼마나 큰 TPR을 얻을 수 있느냐가 중요
• 가운데 직선에서 멀어지고 왼쪽 상단 모서리 쪽으로 가파르게 곡선이 이동할 수록 직사각형에 가까운 곡선이 되어 면적이 1에 가까워지는 좋은 ROC AUC성능 수치를 얻게 됨
• 가운데 대각선 직선은 ACU값으로 0.5이다. 따라서 보통 분류의 AUC 값은 0.5 이상

from sklearn.metrics import roc_auc_score
pred_proba = pipe.predict_proba(X_test)[:,1]
auc_score = roc_auc_score(y_test, pred_proba)
print('ROC AUC 값 : {0:.4f}'.format(auc_score))

출처

N223

출처
출처

confusion_matrix(y_val, y_pred) 코드로 시각화 하기

import matplotlib.pyplot as plt
import seaborn as sns
confusion = confusion_matrix(y_val, y_pred)
sns.heatmap(confusion, fmt= '.0f',cmap="YlGnBu", annot=True)    
plt.title(f'Confusion matrix, n = {len(y_val)}', fontsize=15)
plt.show() 

참고

대각 행렬

np.diag()

랜덤 포래스트에 최적임계값 적용하는 방법

threshold = 0.4
predicted_proba = random_forest.predict_proba(X_test)
predicted = (predicted_proba [:,1] >= threshold).astype('int')
accuracy = accuracy_score(y_test, predicted)

출처