[Dynamic Programming] Floyd Warshall 알고리즘

HOONSSAC·2024년 5월 13일

Java algorithm dijkstra dynamic programming floyd-warshall python

Algorithm

목록 보기

4/8

안녕하세요🐱

오늘은 Dynamic Programming 알고리즘 중 Floyd Warshall 알고리즘에 대해서 한 번 알아보겠습니다.

📌Floyd Warshall 알고리즘이란

Floyd Warshall 알고리즘은 모든 지점에서 다른 모든 지점까지의 최단 경로를 모두 구해야 하는 경우에 사용할 수 있는 Dynamic Programming 알고리즘입니다.

한 지점에서 다른 특정 지점까지의 최단 경로를 구할 때 사용하는 Dijkstra 최단 경로 알고리즘과 최적화 문제를 해결하는 알고리즘이라는 공통점이 있지만, 동작 방식에 있어서 차이점이 있습니다.

그 차이점을 살펴보면서 Floyd Warshall 알고리즘에 대해서 알아보겠습니다.😎

Dijkstra와의 비교

Dijkstra의 경우, 단계마다 최단 거리를 가지는 노드를 하나씩 반복적으로 선택합니다. 그리고 해당 노드를 거쳐가는 경로를 확인하며, 최단 거리 테이블을 갱신하는 방식으로 동작합니다.

이는 매 단계에서 최적의 해를 선택하는 Greedy 알고리즘에 속합니다.

Floyd Warshall의 경우 또한, 단계마다 거쳐 가는 노드를 기준으로 알고리즘을 수행합니다. 하지만, 매번 방문하지 않은 노드 중에서 최단 거리를 갖는 노드를 찾을 필요가 없다는 점이 Dijkstra와의 차이점입니다.

노드의 개수가 $N$ 개일 때 알고리즘 상으로 $N$ 번의 단계를 수행하며, 각 단계마다 $O(N^2)$ 의 연산을 통해 현재 노드를 거쳐 가는 모든 경로를 고려합니다. 따라서, Floyd Warshall 알고리즘의 총 시간 복잡도는 $O(N^3)$ 입니다.

❗그리고 Dijkstra와 한 가지 차이점이 더 있습니다.

Dijkstra 알고리즘에서는 출발 노드가 1개이므로, 다른 모든 노드까지의 최단 거리를 저장하기 위해서 1차원 리스트를 이용합니다. 반면, Floyd Warshall 알고리즘은 모든 노드에 대하여 모든 노드로 가는 최단 거리 정보를 담아야 하기 때문에, 2차원 리스트에 최단 거리 정보를 저장합니다.

📌점화식

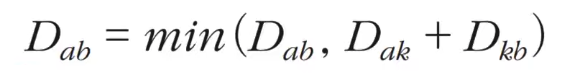
🛠️동작 과정 예시

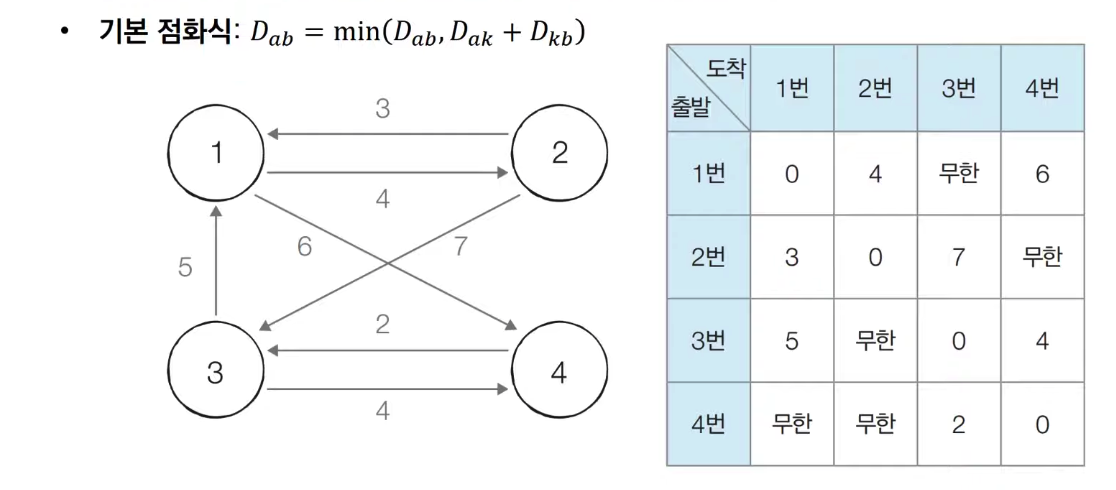
📍초기 상태

그래프를 준비하고 최단 거리 테이블을 초기화합니다.

📍Step 1

1번 노드를 거쳐 가는 경우를 고려하여 테이블을 갱신합니다.

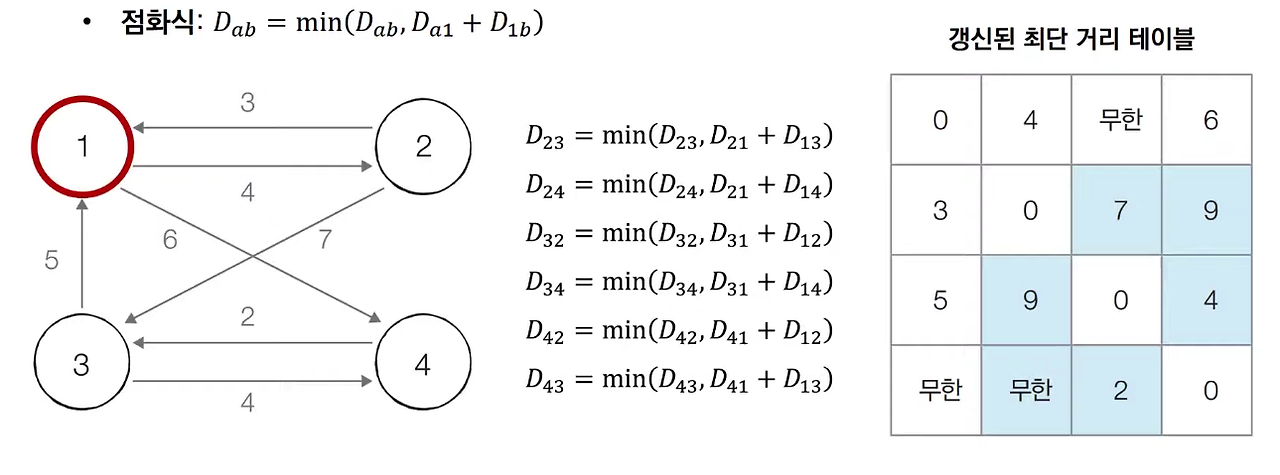
📍Step 2

2번 노드를 거쳐 가는 경우를 고려하여 테이블을 갱신합니다.

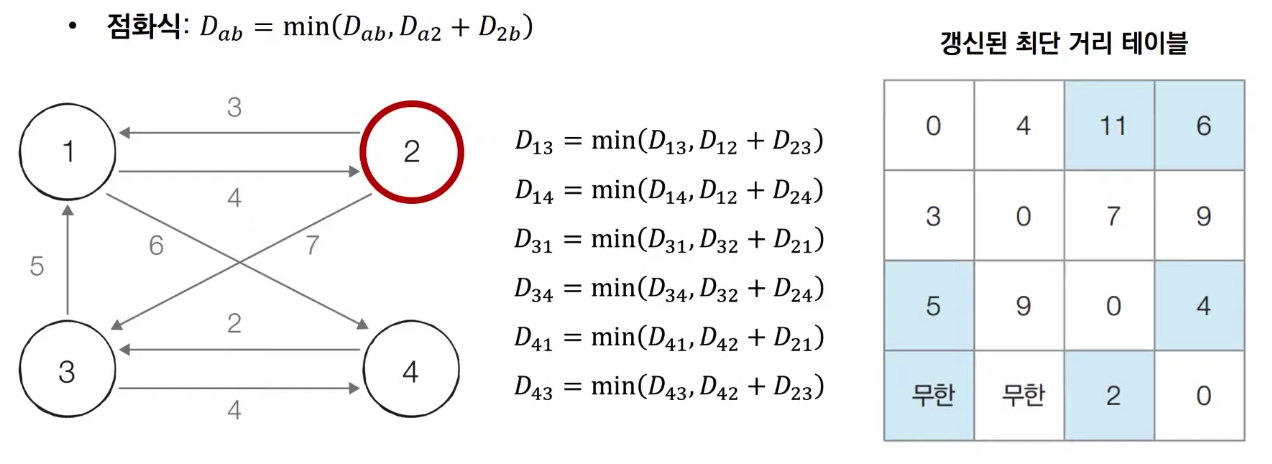
📍Step 3

3번 노드를 거쳐 가는 경우를 고려하여 테이블을 갱신합니다.

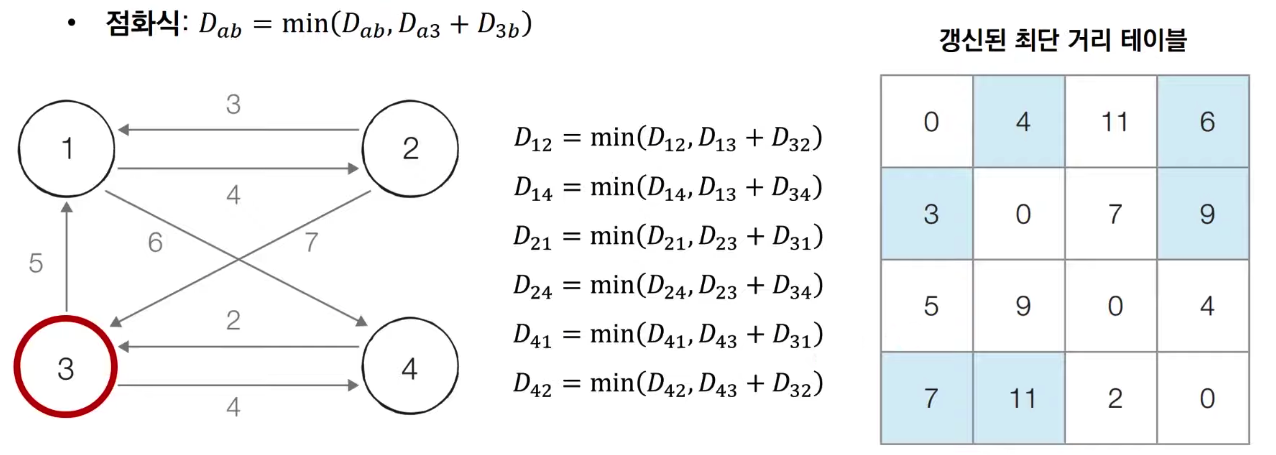
📍Step 4

4번 노드를 거쳐 가는 경우를 고려하여 테이블을 갱신합니다.

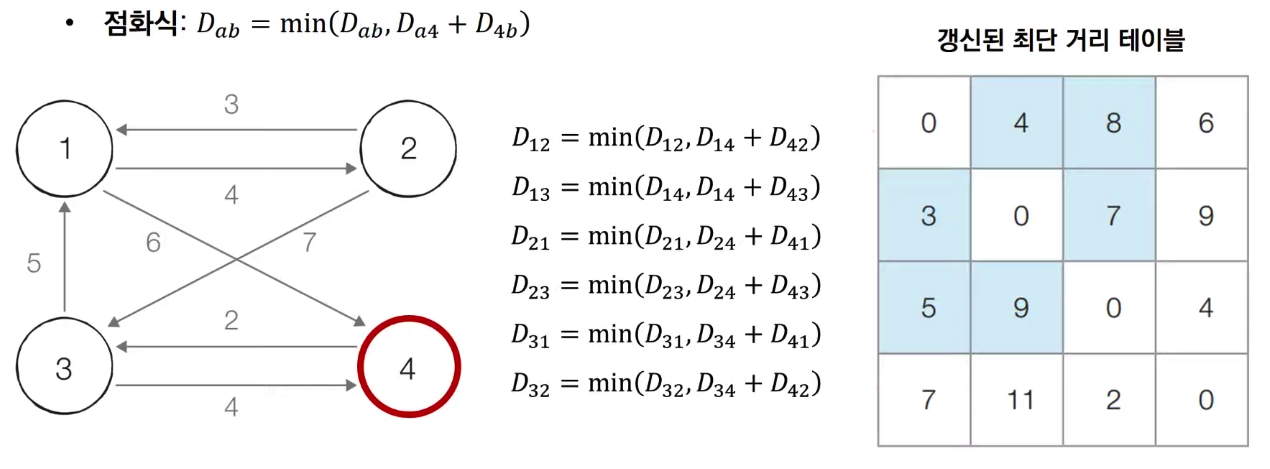
🖥️코드 구현

Python

INF = int(1e9) # 무한을 의미하는 값으로 10억을 설정

# 노드의 개수 및 간선의 개수를 입력받기
n = int(input())
m = int(input())
# 2차원 리스트(그래프 표현)를 만들고, 모든 값을 무한으로 초기화
graph = [[INF] * (n + 1) for _ in range(n + 1)]

# 자기 자신에서 자기 자신으로 가는 비용은 0으로 초기화
for a in range(1, n + 1):
    for b in range(1, n + 1):
        if a == b:
            graph[a][b] = 0

# 각 간선에 대한 정보를 입력 받아, 그 값으로 초기화
for _ in range(m):
    # A에서 B로 가는 비용은 C라고 설정
    a, b, c = map(int, input().split())
    graph[a][b] = c

# 점화식에 따라 플로이드 워셜 알고리즘을 수행
for k in range(1, n + 1):
    for a in range(1, n + 1):
        for b in range(1, n + 1):
            graph[a][b] = min(graph[a][b], graph[a][k] + graph[k][b])

# 수행된 결과를 출력
for a in range(1, n + 1):
    for b in range(1, n + 1):
        # 도달할 수 없는 경우, 무한(INFINITY)이라고 출력
        if graph[a][b] == 1e9:
            print("INFINITY", end=" ")
        # 도달할 수 있는 경우 거리를 출력
        else:
            print(graph[a][b], end=" ")
    print()

Java

import java.util.*;

public class Main {

    public static final int INF = (int) 1e9; // 무한을 의미하는 값으로 10억을 설정
    // 노드의 개수(N), 간선의 개수(M)
    // 노드의 개수는 최대 500개라고 가정
    public static int n, m;
    // 2차원 배열(그래프 표현)를 만들기
    public static int[][] graph = new int[501][501];

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);

        n = sc.nextInt();
        m = sc.nextInt();

        // 최단 거리 테이블을 모두 무한으로 초기화
        for (int i = 0; i < 501; i++) {
            Arrays.fill(graph[i], INF);
        }

        // 자기 자신에서 자기 자신으로 가는 비용은 0으로 초기화
        for (int a = 1; a <= n; a++) {
            for (int b = 1; b <= n; b++) {
                if (a == b) graph[a][b] = 0;
            }
        }

        // 각 간선에 대한 정보를 입력 받아, 그 값으로 초기화
        for (int i = 0; i < m; i++) {
            // A에서 B로 가는 비용은 C라고 설정
            int a = sc.nextInt();
            int b = sc.nextInt();
            int c = sc.nextInt();
            graph[a][b] = c;
        }

        // 점화식에 따라 플로이드 워셜 알고리즘을 수행
        for (int k = 1; k <= n; k++) {
            for (int a = 1; a <= n; a++) {
                for (int b = 1; b <= n; b++) {
                    graph[a][b] = Math.min(graph[a][b], graph[a][k] + graph[k][b]);
                }
            }
        }

        // 수행된 결과를 출력
        for (int a = 1; a <= n; a++) {
            for (int b = 1; b <= n; b++) {
                // 도달할 수 없는 경우, 무한(INFINITY)이라고 출력
                if (graph[a][b] == INF) {
                    System.out.print("INFINITY ");
                }
                // 도달할 수 있는 경우 거리를 출력
                else {
                    System.out.print(graph[a][b] + " ");
                }
            }
            System.out.println();
        }
    }
}