[Dynamic Programming] Edit Distance 알고리즘

HOONSSAC·2024년 5월 25일

algorithm dynamic programming edit distance python

Algorithm

목록 보기

5/8

안녕하세요🐱
오늘은 Dynamic Programming의 종류 중 하나인
Edit Distance 알고리즘에 대해서 한 번 알아보겠습니다.

💡개념

Edit Distance 알고리즘은 두 문자열 사이의 유사도를 판단하는 알고리즘입니다.

문자열 사이의 유사도란 여기서는 Distance 즉, 거리를 의미하는데요,
여기서의 거리란, 문자열을 다른 문자열로 변환하기 위해 필요한 최소한의 편집 연산(삽입, 삭제, 수정)의 수를 의미합니다.

Edit Distance 알고리즘은 Dynamic Programming 기법을 사용하여 바로 이 문자열 사이의 거리를 측정하는 데 사용됩니다.

🧮연산

먼저 사용할 수 있는 3가지 연산에 대해서 알아보겠습니다.

삽입(insert)

주어진 문자열이 아래와 같을 경우,
s1 : ab
s2 : abc
s1의 맨 끝에 c를 삽입(insert)해서 str2로 바꿀 수 있다.

삭제(remove)

주어진 문자열이 아래와 같을 경우,
s1 : wxyz
s2 : xy
s1에서 w와 z를 삭제(remove)해서 str2로 바꿀 수 있다.

수정(modify)

주어진 문자열이 아래와 같을 경우,
s1 : chiduen
s2 : chicken
s1에서 d와 u를 c와 k로 수정(modify)해서 str2로 바꿀 수 있다.

🛠️과정

초기화

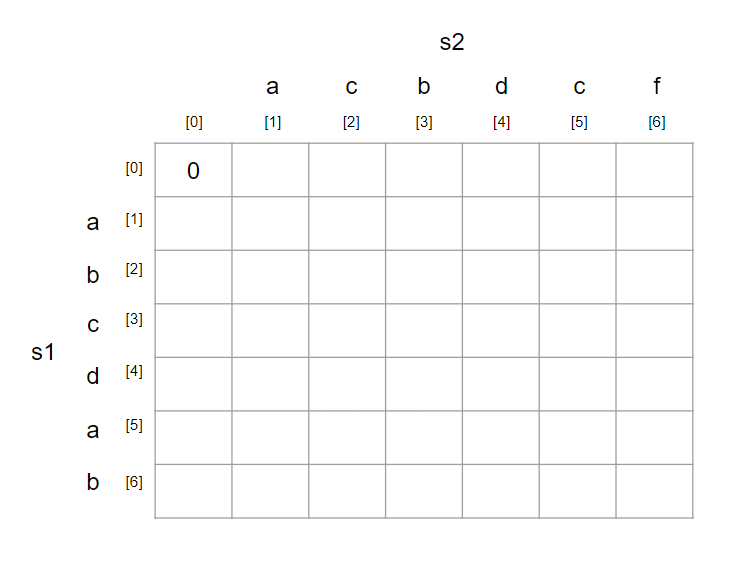
초기 표의 상태는 다음과 같습니다.

(0, 0)은 문자가 없는 빈 문자열을 의미합니다.
(0, 0)은 0으로 초기화를 해줍니다.

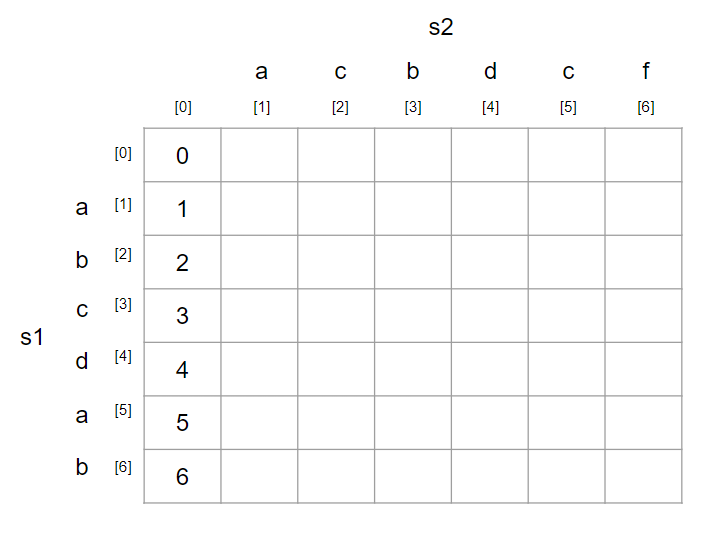
0번째 열은 s1을 빈 문자열로 바꿀 때 필요한 연산의 횟수를 의미합니다.
즉, 삭제(remove)연산을 몇 번 해야하는지를 채우면 됩니다.

0번째 행은 빈 문자열을 s2로 바꿀 때 필요한 연산의 횟수를 의미합니다.
즉, 삽입(insert)연산을 몇 번 해야하는지를 채우면 됩니다.

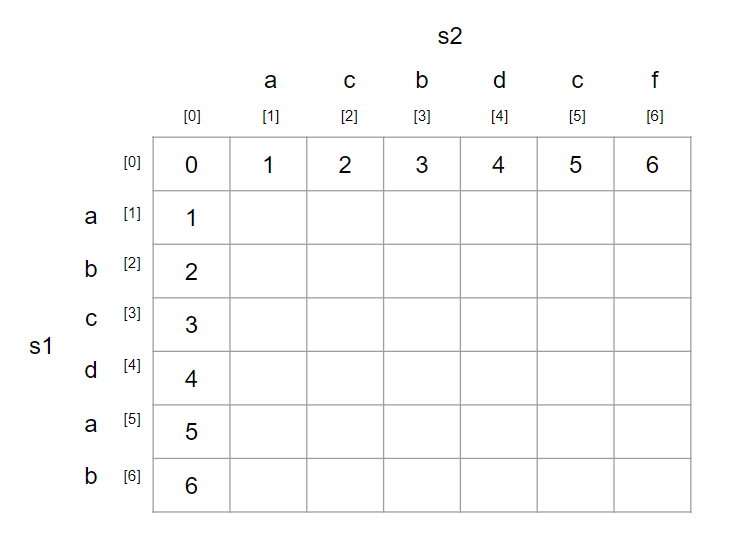
이렇게 해서 DP 테이블의 초기화 과정이 끝났습니다.

🚩알고리즘 설명

s1에서 i번째 문자와 s2에서 j번째 문자를 서로 비교합니다.

두 문자가 같은 경우, 별도의 연산을 수행할 필요가 없기 때문에 dp[i-1][j-1]의 값을 그대로 가져옵니다.

두 문자가 다른 경우, dp[i-1][j], dp[i][j-1], dp[i-1][j-1] 중 최소값에 1을 더해서 dp[i][j]에 저장합니다.

🛠️알고리즘 적용

(1, 1)부터 보겠습니다.
s1[1] = s2[1]이므로, 별도의 연산 없이 (0, 0)의 값을 가져옵니다.

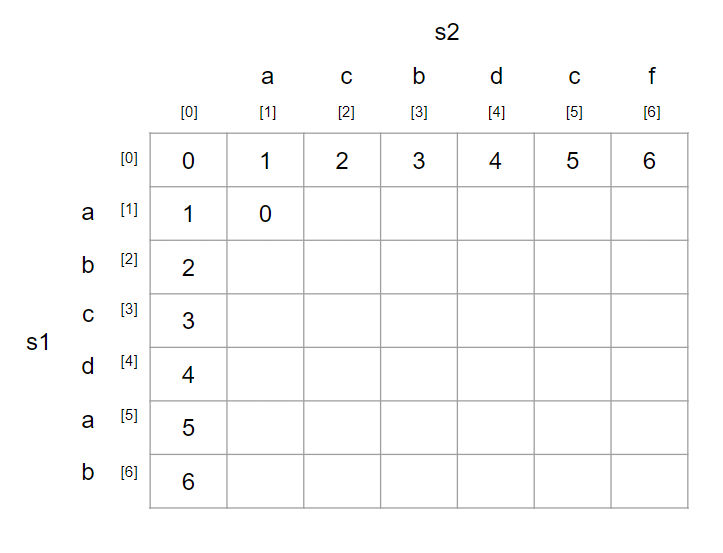
다음으로 (1, 2)를 보겠습니다.
s1[1] = a, s2[2] = c이므로 연산이 필요합니다.

앞서 언급한 3가지 연산의 각각 연산 횟수를 살펴보겠습니다.

삽입 : dp[1][1] + 1 = 1
삭제 : dp[0][2] + 1 = 3
수정 : dp[0][1] + 1 = 2

결과적으로 제일 최소인 삽입 연산을 수행하게 됩니다.

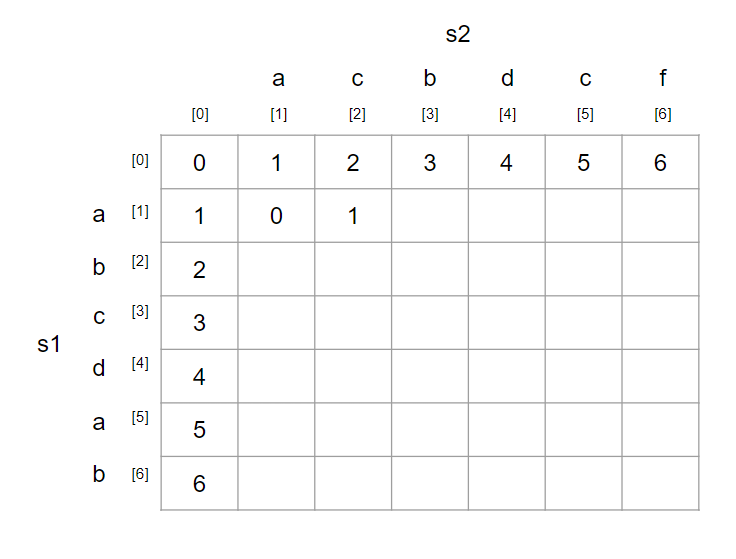
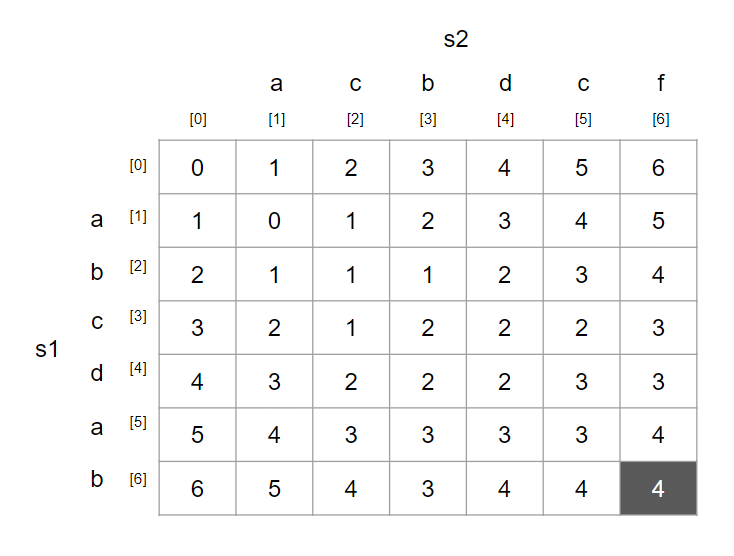
위의 과정을 반복하면, 최종적으로 표가 완성됩니다.
여기서 우리가 구하고자 하는 값은 맨 오른쪽 아래의 값이 됩니다.

🛠️코드로 구현

def edit_dist(a, b):
    n = len(a)
    m = len(b)
    
    # DP 테이블 초기화
    dp = [[0] * (m + 1) for _ in range(n + 1)]

    # DP 테이블 초기 설정
    for i in range(1, n + 1):
        dp[i][0] = i

    for j in range(1, m + 1):
        dp[0][j] = j

    # 최소 편집 거리 계산
    for i in range(1, n + 1):
        for j in range(1, m + 1):
            
            # 문자가 같다면, 왼쪽 위에 해당하는 수를 그대로 대입
            if a[i - 1] == b[j - 1]:
                dp[i][j] = dp[i - 1][j - 1]
                
            # 문자가 다르다면, 3가지 경우 중에서 최솟값을 대입
            # 삽입(왼쪽), 삭제(위쪽), 교체(왼쪽 위) 중에서 최소 비용을 찾는다.
            else:
                dp[i][j] = min(dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]) + 1
                
    return dp[n][m]