[Greedy] Kruskal, Prim 알고리즘으로 MST 구현하기

HOONSSAC·2024년 4월 5일
CMSTalgorithmgreedykruskalprim
1

Algorithm

목록 보기
3/8
post-thumbnail

안녕하세요👻
오늘은 대표적인 MST(Minimum Spanning Tree)알고리즘인 Kruskal과 Prim에 대해서 알아보고 직접 구현까지 해보겠습니다!

MST(Minimum Spanning Tree)

Spanning Tree

Spanning Tree란, 무방향 그래프 G(V,E)에서 E에 속한 간선들로 사이클을 포함하지 않으면서 모든 정점 V를 연결한 부분 그래프를 뜻합니댜.

그래프에서 Spanning Tree는 여러 형태로 존재할 수 있으며, Spanning Tree의 특징은 n개의 정점을 갖는 그래프에서 Spanning Tree에 속하는 간선의 수는 n−1n-1개이며 사이클을 이루지 않는다는 특징이 있습니다.

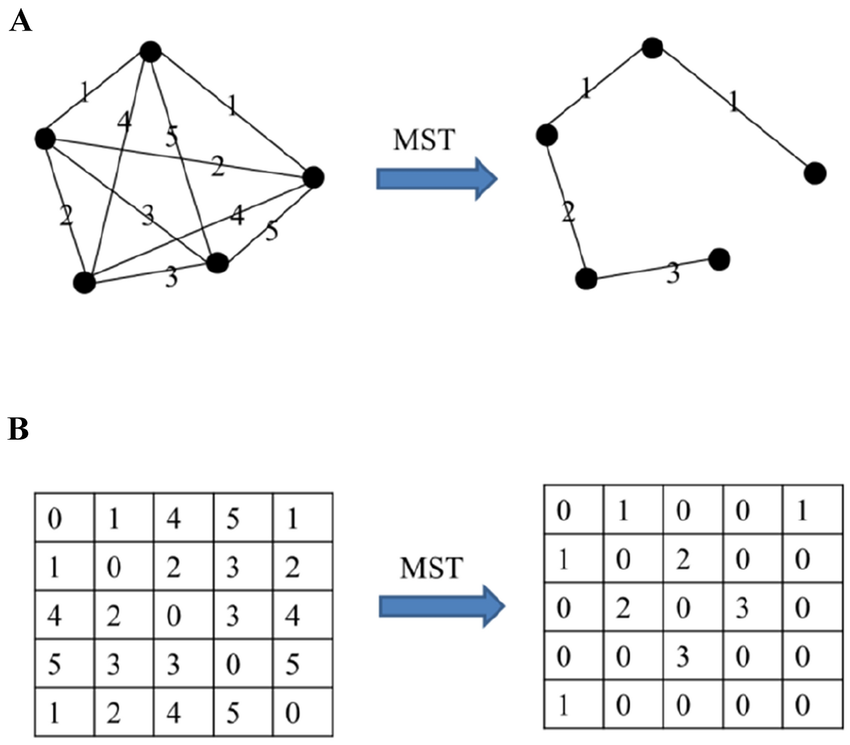
그리고 MST란, 최소 비용 신장 트리(이하 최소 신장 트리)를 뜻하며, 무방향 그래프의 간선들에 가중치가 주어진 경우, 여러 신장 트리 중에 간선들의 가중치 합이 최소인 신장 트리를 말합니다.

Kruskal

Kruskal은 이 MST의 대표적인 알고리즘입니다.

Kruskal은 결정의 순간마다 최선의 결정을 함으로써 모든 정점을 최소 비용으로 연결하여 최소 신장 트리를 구하는 알고리즘입니다.

이 Kruskal의 핵심은 모든 간선을 가중치 기준으로 오름차순으로 정렬하고,

이 간선들을 순서대로 모든 정점이 연결될 때까지 연결하는 것입니다.

Union-Find 알고리즘을 이용해서 구현할 수 있고, 이를 통해 사이클이 형성되지 않으면서 모든 정점을 연결할 수 있습니다.

동작 방식

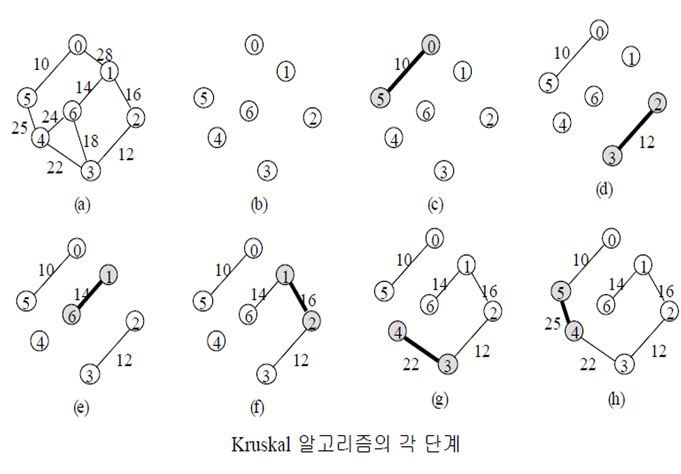
  1. 그래프의 간선들을 가중치 기준 오름차순으로 정렬합니다.

  2. 정렬된 간선 리스트를 순서대로 선택하여, 간선의 정점들을 연결합니다. 이때 정점을 연결하는 것은 Union-Find의 Union으로 구현합니다.

  3. 만약 간선의 두 정점 a,b가 이미 연결되어 있다면 스킵해줍니다.

  4. 위의 과정을 반복하여 최소 비용의 간선들만 이용하여 모든 정점이 연결됩니다.

Prim

Prim도 앞에서 언급한 최소 신장 트리를 구하는 알고리즘입니다.

Prim은 임의의 시작점에서 현재까지 연결된 정점들에서 연결되지 않은 정점들에 대해, 가장 가중치가 작은 정점을 연결하는 정점 선택 기반으로 동작합니다.

Prim의 핵심은 트리 집합을 단계적으로 확장하는 것이고, 새로운 정점을 연결할 때마다 새로운 정점에서 갈 수 있는 아직 연결되지 않은 정점들에 대한 간선을 추가해줘야 합니다.

동작 방식

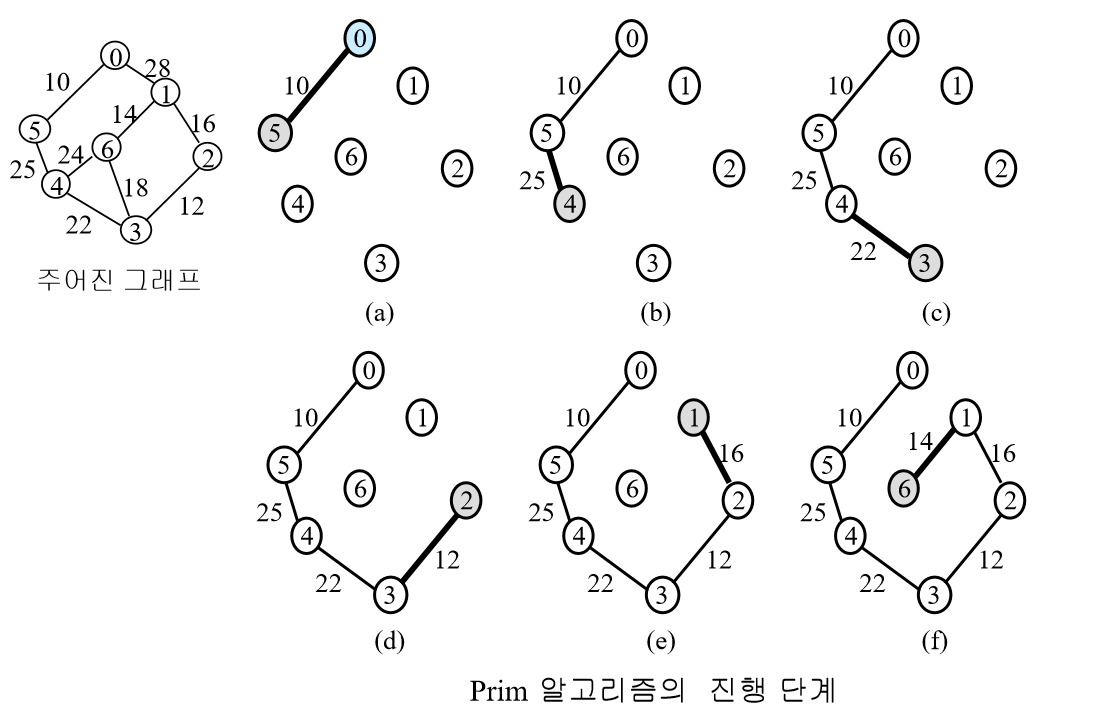
  1. 임의의 정점을 시작점으로 선택합니다.

  2. 시작점에서 갈 수 있는 정점 중 가장 가중치가 작은 정점을 연결합니다.

  3. 시작점과 연결된 정점들을 a집합이라 할 때, a집합에서 갈 수 있는 a집합에 속하지 않은 정점들에 대해 가중치가 가장 작은 정점을 연결합니다.

  4. 위의 과정을 모든 정점이 연결될 때까지 반복합니다.

이 알고리즘들을 처음 접하신 분들은 이 설명만으로는 이해하기 어려우시겠지만, 저는 시간 관계상 이렇게 간략하게만 정리하고 넘어가겠습니다😂
(검색해보시면 더 친절하고 자세한 설명들이 많습니다!)

최종 구현

setting.h

// 공통적으로 사용되는 설정값들을 정의한 헤더 파일
#ifndef SETTING_H
#define SETTING_H

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <string.h>
#include <limits.h>

#define VERTEX_COUNT 11 // 정점의 수
#define EDGE_COUNT 10 // 간선의 수

// 간선 구조체 선언
typedef struct {
    int node[2];
    int distance;
} Edge;

#endif

main.c

#include <stdio.h>
#include <windows.h>
#include "Kruskal.h"
#include "Prim.h"

int main(void){
    srand(time(NULL));

    int n = VERTEX_COUNT; // 정점의 수
    int m = EDGE_COUNT; // 간선의 수

    LARGE_INTEGER frequency; // 초당 카운트
    LARGE_INTEGER start, end; // 시작 및 종료 값
    double elapsedTime; // 실행 시간

    // 초당 카운트 획득
    QueryPerformanceFrequency(&frequency);
    QueryPerformanceCounter(&start);

    //KruskalMST(n, m); //....Kruskal을 사용할 때 활성화
    //PrimMST(n, m); //........Prim을 사용할 때 활성화

    QueryPerformanceCounter(&end); // 종료 시간 획득
    // 실행 시간 계산
    elapsedTime = (double)(end.QuadPart - start.QuadPart) / frequency.QuadPart;
    // 실행 시간 출력
    printf("Execution time: %f seconds\n", elapsedTime);

    return 0;
}

Kruskal.h

#include "setting.h"

// 부모 노드를 찾는 함수
int getParent(int parent[], int x){
    if(parent[x] == x)
        return x;
    return parent[x] = getParent(parent, parent[x]);
}

// 두 부모 노드를 합치는 함수
void unionParent(int parent[], int a, int b){
    a = getParent(parent, a);
    b = getParent(parent, b);
    if(a < b) parent[b] = a;
    else parent[a] = b;
}

// 같은 부모를 가지는지 확인
int findParent(int parent[], int a, int b){
    a = getParent(parent, a);
    b = getParent(parent, b);
    if(a == b)
        return 1;
    return 0;
}

// 간선 비교 함수
int compare(const void* a, const void* b){
    Edge* edgeA = (Edge*)a;
    Edge* edgeB = (Edge*)b;
    if(edgeA->distance > edgeB->distance) return 1;
    else if(edgeA->distance < edgeB->distance) return -1;
    else return 0;
}

void KruskalMST(int n, int m) {
    Edge edges[m]; // 간선 정보를 저장할 배열

    int exists[EDGE_COUNT][EDGE_COUNT]; // 이미 존재하는 간선을 확인하기 위한 배열, 정점의 수 + 1로 크기 설정
    memset(exists, 0, sizeof(exists)); // exists 배열을 0으로 초기화

    printf("Random Matrix Generation !!\n");

    for(int i = 0; i < m; i++) { // m개의 간선 생성을 위한 반복문
        int a, b, weight;
        do {
            a = rand() % n + 1;
            b = rand() % n + 1;
            weight = rand() % 20 + 1; // 가중치도 여기서 생성
        } while (a == b || exists[a][b]); // a와 b가 같지 않고, 해당 간선이 이미 존재하지 않을 때까지 반복
        
        // 새로운 간선을 배열에 추가
        edges[i].node[0] = a;
        edges[i].node[1] = b;
        edges[i].distance = weight;

        exists[a][b] = exists[b][a] = 1; // 간선이 존재함을 표시
        printf("%d. random edge : (%d,%d), (%d,%d), weight: %d\n", i+1, a, b, b, a, weight);
    }

    // 간선의 비용을 기준으로 오름차순 정렬
    qsort(edges, m, sizeof(Edge), compare);

    int parent[n+1]; // 인덱스를 1부터 사용하기 위해 n+1 크기로 선언
    for(int i = 1; i <= n; i++){
        parent[i] = i;
    }

    int sum = 0;

    int adjacencyMatrix[n][n]; // 인접 행렬 초기화
    memset(adjacencyMatrix, 0, sizeof(adjacencyMatrix));

    for(int i = 0; i < m; i++){
        if(!findParent(parent, edges[i].node[0], edges[i].node[1])){
            sum += edges[i].distance;
            unionParent(parent, edges[i].node[0], edges[i].node[1]);
            // 인접 행렬에 간선의 가중치를 추가합니다. 양방향으로 표시
            adjacencyMatrix[edges[i].node[0] - 1][edges[i].node[1] - 1] = edges[i].distance;
            adjacencyMatrix[edges[i].node[1] - 1][edges[i].node[0] - 1] = edges[i].distance;
        }
    }

    printf("\nNumber of Vertices: %d\n", n);
    printf("Number of Edges: %d\n\n", m);

    printf("Adjacency Matrix of Direct Graph\n");
    for(int i = 0; i < n; i++){
        for(int j = 0; j < n; j++){
            printf("%3d ", adjacencyMatrix[i][j]);
        }
        printf("\n");
    }
}

Prim.h

#include "setting.h"

// 최소 가중치 간선을 찾는 함수
int minKey(int key[], int mstSet[], int n) {
    int min = INT_MAX, min_index = -1; // min_index를 -1로 초기화
    for (int v = 0; v < n; v++)
        if (mstSet[v] == 0 && key[v] < min)
            min = key[v], min_index = v;
    return min_index;
}

// 프림 알고리즘
void Prim(int n, int graph[n][n]) {
    int parent[n]; // 최소 스패닝 트리를 저장할 배열
    int key[n]; // 최소 가중치를 저장할 배열
    int mstSet[n]; // MST 집합에 포함된 노드를 표시하는 배열

    // 초기화
    for (int i = 0; i < n; i++)
        key[i] = INT_MAX, mstSet[i] = 0;

    key[0] = 0; // 첫 번째 정점을 시작점으로 선택
    parent[0] = -1; // 첫 번째 정점은 MST의 루트이므로 부모가 없음

    for (int count = 0; count < n - 1; count++) {
        int u = minKey(key, mstSet, n);
        mstSet[u] = 1;

        for (int v = 0; v < n; v++)
            if (graph[u][v] && mstSet[v] == 0 && graph[u][v] < key[v])
                parent[v] = u, key[v] = graph[u][v];
    }

}

void PrimMST(int n, int m){

    int graph[n][n]; // 인접 행렬 초기화

    memset(graph, 0, sizeof(graph)); // graph 배열을 0으로 초기화

    printf("Random Matrix Generation !!\n");

    for (int i = 0; i < m; i++) { // m개의 간선 생성을 위한 반복문
        int a, b, weight;
        do {
            a = rand() % n;
            b = rand() % n;
            weight = rand() % 20 + 1; // 가중치도 여기서 생성
        } while (a == b || graph[a][b]); // a와 b가 같지 않고, 해당 간선이 이미 존재하지 않을 때까지 반복
        
        // 새로운 간선을 배열에 추가
        graph[a][b] = weight;
        graph[b][a] = weight; // 무방향 그래프이므로 양쪽에 가중치 추가
        printf("%d. random edge : (%d,%d), weight: %d\n", i+1, a, b, weight);
    }

    printf("\nNumber of Vertices: %d\n", n);
    printf("Number of Edges: %d\n\n", m);

    // 인접 행렬 출력
    printf("\nGenerated Adjacency Matrix:\n");
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            printf("%3d ", graph[i][j]); // 각 값 출력
        }
        printf("\n"); // 행이 끝나면 새로운 줄로
    }

    // 프림 알고리즘 실행
    Prim(n, graph);
}

실행 결과

Kruskal

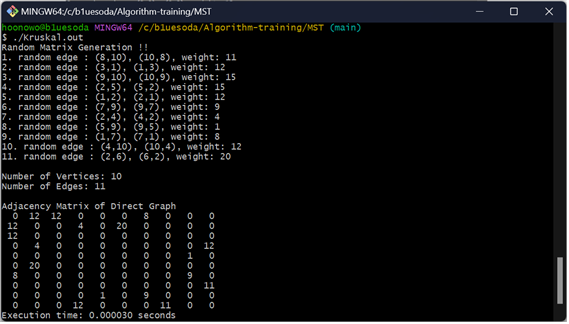
Prim

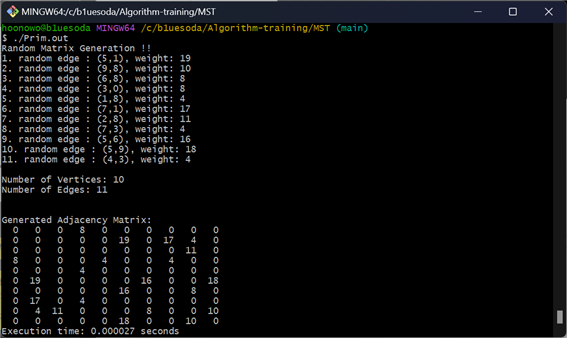
Vertex를 증가시켜 본 결과

Kruskal

Prim

고찰 및 결론

주어진 조건들을 바탕으로 Kruskal과 Prim 알고리즘을 각각 구현해 실행해 본 결과, Prim 알고리즘이 Kruskal 알고리즘보다 더 빠르게 측정되었습니다.

게다가 정점과 간선의 수가 커질수록 더 큰 차이를 보여주었습니다. 이를 통해 알 수 있는 점은 그래프의 밀도가 높을수록 Prim 알고리즘이 Kruskal 알고리즘보다 더 효율적이라는 것입니다.

그리고 정점의 수에 비해 간선의 수가 많은 경우, Kruskal 알고리즘은 모든 간선을 처음에 정렬해야 하므로 비효율적일 수 있겠다는 생각이 들었습니다. 반면, Prim 알고리즘은 각 단계에서 MST에 인접한 간선만을 고려하기 때문에, 이러한 상황에서는 더 나은 성능을 보여준 게 아닐까 추측해볼 수 있습니다😉

📚Reference
The example to explain the MST algorithm
Kruskal과 Prim

🚩Source Code
Algorithm-training

profile
HOONSSAC
훈싹의 개발여행
이전 포스트

[Divide and Conquer] Selection 알고리즘 구현하기

다음 포스트

[Dynamic Programming] Floyd Warshall 알고리즘

0개의 댓글