시각화/통계학

Andrew·2021년 1월 29일

[Contents]

1) 시각화 도구
2) 통계학 맛보기

시각화 도구

가장 대중적으로 많이 쓰이는 matplotlib, seaborn 모듈에 대해 학습

matplotlib

다소 복잡한 라이브러리 구성으로 인해 최근에는 그 사용 빈도와 대중성이 떨어지고 있으나 여전히 많은 입문자들이 청므 사용해보게 되는 좋은 시각화 라이브러리

seaborn

모든 기능을 matplotlib을 기반으로 제공되어 matplotlib과 상호 호환된다

matplotlib의 모든 기능을 사용하면서 손 쉽게 사용하고 싶다면 seaborn이 가장 적절한 대안

matplotlib overview

pyplot 객체를 사용하여 데이터를 표시
최대 단점 : argument를 kwargs 받음
고정된 argument 가 없어서 alt+tab으로 확인 어려움
graph는 원래 figure 객체에 생성됨
pyplot 객체 사용시, 기본 figure에 그래프가 그려짐
figure & Axes
- matplotlib은 figure안에 axes로 구성
- figure위에 여러개의 axes를 생성

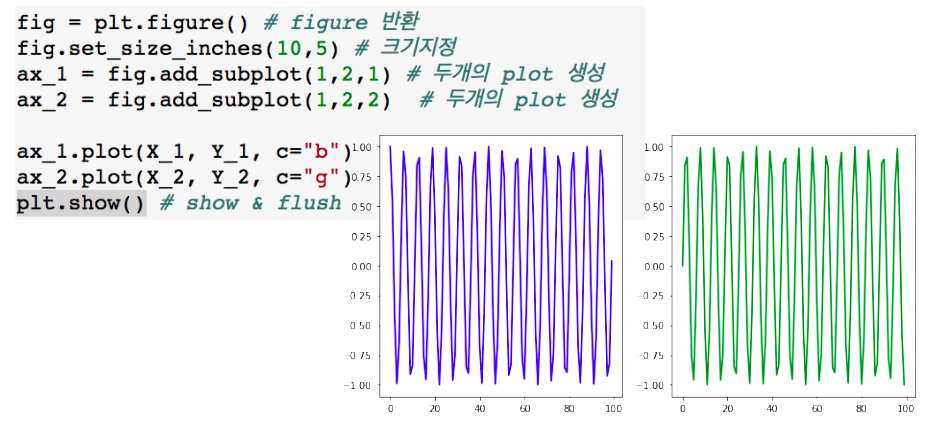
set color

color 속성을 사용
float : 흑백, rgb color, predefined color 사용

set legend

legend 함수로 범례를 표싷마, loc위치 등 속성 지정

plt.plot(x_1, Y_1, color='b', linestype='dashed', label='line_1')
plt.plot(X_2, Y_2, color='r', linestype='dotted', label='line_2')
plt.legend(shadow=True, fancybox=True, loc = 'lower right')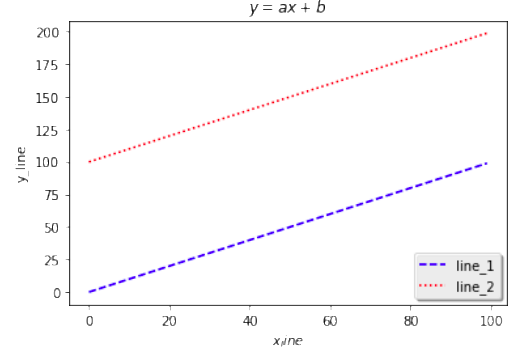

seaborn

기존 matplotlib에 기본 설정을 추가
복잡한 그래프를 간단하게 만들 수 있는 wrapper
간단한 코드 + 예쁜 결과
lineplot, scatterplot, countplot 등

seaborn predefined plots

Violinplot - boxplot에 distribution을 함께 표현
Stripplot - scatter와 category 정보를 함께 표현
Swarmplot- 분포와 함께 scatter를 함께 표현
Pointplot - categor 별로 numeri의 평균, 신뢰구간 표시
regplot - scatter + 선형함수를 함께 표시

통계학 맛보기

모수의 개념과 모수를 측정하는 방법으로 최대가능도 추정법 을 소개

정규분포, 카테고리분포에서의 예제로 최대가능도 추정법을 설명

표본분포와 표집분포, 가능도(likelihood)와 확률 등 헷갈릴 수 있는 개념들이 많이 소개되므로 각각의 정확한 의미와 차이점을 충분히 공부

최대가능도 추정법을 통해 정답에 해당하는 확률분포와 모델이 추정하는 확률분포의 거리를 최소화함으로써 모델을 학습시킬 수 있으며, 이 원리는 딥러닝/머신러닝에서 유용하게 사용된다

Further Question

1) 확률과 가능도의 차이가 무엇일까요? (개념적인 차이, 수식에서의 차이, 확률밀도함수에서의 차이)
2) 확률 대신 가능도를 사용하였을 때의 이점은 어떤 것이 있을까요?
3) 다음의 code snippet은 어떤 확률분포를 나타내는 것일까요? 해달 확률분포에서 변수가 theta가 의미할 수 있는 것은 무엇이 있을까요?

import numpy as np
import matplotlib.pyplot as plt
theta = np.arange(0,1,0.001)
p = theta ** 3 * (1 - theta) ** 7
plt.plot(theta, p)
plt.show()

모수가 뭐예요?

통계적 모델링은 적절한 가정 위에서 확률분포를 추정(inference) 하는 것이 목표이며, 기계학습과 통계학이 공통적으로 추구하는 목표이다
그러나 유한한 개수의 데이터만 관찰해서 모집단의 분포를 정확하게 알아낸다는 것은 불가능하므로, 근사적으로 확률분포를 추정 할 수 밖에 없다
- 예측모형의 목적은 분포를 정확하게 맞추는 것보다는 데이터와 추정 방법의 불확실성을 고려해서 예측의 위험을 최소화하는 것이다
- 모집단 : 정보를 얻고자 하는 관심 대상의 전체집합
데이터가 특정 확률분포를 따른다고 선험적으로(a priori) 가정한 후 그 분포를 결정하는 모수(parameter)를 추정하는 방법은 모수적(parametric) 방법론 이라 한다
- 모수 : 평균과 분산을 묶어서 모수라 부른다
특정 확률분포를 가정하지 않고 데이터에 따라 모델의 구조 및 모수의 개수가 유연하게 바뀌면 비모수(nonparametric) 방법론 이라 부른다
- 기계학습의 많은 방법론은 비모수 방법론에 속한다
- 주의사항! : 비모수는 모수가 없다는 의미가 아니라 모수가 무한이 많거나 모수의 갯수가 데이터의 따라서 바뀌는것이 비모수 방법론이다

확률분포를 가정하는 방법

우선 히스토그램을 통해 모양을 관찰
- 데이터가 2개의 값(0 또는 1)만 가지는 경우 -> 베르누이 분포
- 데이터가 n개의 이산적인 값을 가지는 경우 -> 카테고리 분포
- 데이터가 [0, 1] 사이에서 값을 가지는 경우 -> 베타 분포
- 데이터가 0 이상의 값을 가지는 경우 -> 감마 분포, 로그정규 분포 등
- 데이터가 R 전체에서 값을 가지는 경우 -> 정규 분포, 라플라스 분포 등
주의! : 기계적으로 확률분포를 가정해서는 안되며, 데이터를 생성하는 원리를 먼저 고려하는 것이 원칙 이다
- 각 분포마다 검정하는 방법들이 있으므로 모수를 추정한 후에는 반드시 검정을 해야한다

데이터로 모수를 추정해보자

데이터의 확률분포를 가정했다면 모수를 추정해볼 수 있다
정규분포의 모수는 평균 $\mu$ 과 분산 $\sigma^2$ 으로 이를 추정하는 통계량(statistic)은 다음과 같다:

표본분산과 표본평균을 정의를 하게 되면 주어진 데이터를 가지고 데이터의 확률분포의 모수를 추정해 볼 수 있고
추정된 모수를 가지고 원래 데이터에서의 성질, 정보들을 취합할 수 있으며
이를 통해 예측 또는 의사결정을 내릴때 사용할 수 있다
통계량의 확률분포를 표집분포(sampling distribution) 라 부르며, 특히 표본평균의 표집분포는 N이 커질수록(데이터를 많이 모을수록) 정규분포 $\mathcal{N}(\mu$ , $\sigma^2 \over N$ ) 를 따른다
- 이를 중심극한정리(Central Limit Theorem) 이라 부르며, 모집단의 분포가 정규분포를 따르지 않아도 성립한다
- 표집분포 : 표본평균과 표본분산의 확률분포

최대가능도 추정법

reference
표본평균이나 표본분산은 중요한 통계량이지만 확률분포마다 사용하는 모수가 다르므로 적절한 통계량이 달라지게 된다
이론적으로 가장 가능성이 높은 모수를 추정하는 방법 중 하나는 최대가능도 추정법(maximum likelihood estimation, MLE) 이다
- $\hat{\theta}_{MLE}$ = $\underset{\theta}{argmax} L(\theta; \mathrm{x})$ = $\underset{\theta}{argmax} P(\mathrm{X}|\theta)$
  - 가능도(likelihood) 함수는 모수 $\theta$ 를 따르는 분포가 $\mathcal{x}$ 를 관찰할 가능성을 뜻하지만 확률로 해석하면 안된다
데이터 집합 $\mathrm{X}$ 가 독립적으로 추출되었을 경우 로그가능도를 최적화 한다
- $L(\theta ; \mathrm{X}) =$ $\prod_{i=1}^n p(x_i|\theta) \Rightarrow log L(\theta ; \mathrm{X}) = \sum_{i=1}^n log P(x_i|\theta)$
- 이런경우 로그함수의 성질(곱을 덧셈으로 바꿔준다)을 이용해서 likelihood 에 로그를 씌어주게 되면 곱셈으로 정의된 확률분포 함수들을 로그 확률분포들의 덧셈으로 바꿀수 있다

왜 로그가능도를 사용하나?

로그가능도를 최적화하는 모수 $\theta$ 는 가능도를 최적화하는 MLE가 된다
데이터의 숫자가 적으면 상관없지만 만일 데이터의 숫자가 수억 단위가 된다면 컴퓨터의 정확도로는 가능도를 계산하는 것은 불가능하다
데이터가 독립일 경우, 로그를 사용하면 가능도의 곱셈을 로그가능도의 덧셈으로 바꿀 수 있기 때문에 컴퓨터로 여난이 가능해진다
경사하강법으로 가능도를 최적화할 때 미분 연산을 사용하게 되는데, 로그 가능도를 사용하면 연산량을 $O(n^2)$ 에서 $O(n)$ 으로 줄여준다
대게의 손실함수의 경우 경사하강법을 사용하므로 음의 로그가능도(negative log-likelihood)를 최적화 하게 된다

확률 vs 가능도

확률(probability) 는 주어진 확률분포에 대해서 특정사건(event)또는 관측값에 대한 확률을 나태내는 것이다
따라서 확률분포는 고정되어있는 상태이고 그러한 상황에서 관측에 대한 확률을 구하는 것이다
이를 조건부 확률의 표기를 빌려 표현하면 다음과 같다
확률 = $P(사건 E | 확률분포 D)$
이와 반대로 가능도(Likelihood) 는 어떤 사건에 대한 관측값이 주어졌을 때(고정), 이 관측이 해당 확률분포에서부터 나왔을 가능성에 대한 확률이다
이에 대해 조건부 확률의 표기를 빌리면 다음과 같다
가능도 = $L(확률분포 D | 사건 E)$
이 경우 고정되어 있는 관측값에 대해 확률분포 그래프의 y값(함수값)을 읽음으로써 서오 다른 확률분포의 경우 가능도를 비교할 수 있다

최대가능도 추정법 예제 : 정규분포(연속확률변수)

정규분포를 따르는 확률번수 $\mathrm{X}$ 로부터 독립적인 표본 { $x_1, ..., x_n$ }을 얻었을 때 최대가능도 추정법을 이용하여 모수를 추정하면?(로그가능도 추정)
- $\hat{\theta}_{MLE}$ = $\underset{\theta}{argmax} L(\theta; \mathrm{x})$ = $\underset{\mu, \sigma^2}{argmax} P(\mathrm{X}|\mu, \sigma^2)$
- $log L(\theta;\mathrm{X}) = \sum_{i=1}^n log P(x_i|\theta) = \sum_{i=1}^n log$ $1 \over \sqrt{2\pi\sigma^2}$ $e^{-|x_i-\mu|^2 \over 2\sigma^2}$ = - $n \over 2$ $log2\pi\sigma^2 - \sum_{i=1}^n$ $|x_i - \mu|^2 \over 2\sigma^2$
$\theta = (\mu, \sigma)$ 에 대해 오른쪽 수식을 미분해서 최적화를 할 수 있다
주어진 로그가능도로 $(\mu, \sigma)$ 를 미분해주게 되면 다음과 같다
- 0 = $\partial log L \over \partial \mu$ = - $\sum_{i=1}^n$ $x_i - \mu \over \sigma^2$ $\Rightarrow \hat{\mu}_{MLE} =$ $1 \over n$ $\sum_{i=1}^n x_i$
- 0 = $\partial log L \over \partial \sigma$ = - $n \over \sigma$ + $1 \over \sigma^3$ $\sum_{i=1}^n |x_i - \mu|^2$ $\Rightarrow \hat{\sigma}^2_{MLE} =$ $1 \over n$ $\sum_{i=1}^n (x_i-\mu)^2$
- 두 미분이 모두 0 이 되는 $\mu, \sigma$ 를 찾으면 로그가능도를 최대화해주는 모수를 찾게 된다
- MLE 는 불편추정량을 보장하진 않는다
- 최대가능도 추정법으로 구한 분산은 n-1 이 아닌 n으로 나눠주게 된다

자유도, 불편추정량

자유도 : 독립변수의 개수

ex) 변수가 3개인 등식은, 2개의 값이 결정되면 나머지 하나의 값이 자동으로 결정된다
따라서 이 경우 독립변수는 2개, 종속변수는 1개이므로 자유도는 2가 된다

불편추정량

추정량의 기대값이 모수와 같아진다면, 이 추정량을 불편추정량이라 한다
- 표본평균의 기대값은 모평균과 같으므로 불편추정량이다
- 표본분산의 기대값은 모분산과 다르므로 불편추정량이 아니다(n으로 나누어서 구한다면)

표본분산을 구할 때 n이 아닌 n-1로 나누는 이유

표본분산을 불편추정량으로 만들어주기 위해 n이 아닌 n-1로 나눈다

최대가능도 추정법 예제 : 카테고리 분포(이산확률변수)

카테고리 분포 Multinoulli( $\mathrm{x};p_i, ..., p_d$ )를 따르는 확률변수 $\mathrm{X}$ 로 부터 독립적인 표본 { $x_i, ..., x_n$ }을 얻었을 때 최대가능도 추정법을 이용하여 모수를 추정하면?
- $\hat{\theta}_{MLE}$ = $\underset{p_1,...,p_d}{argmax}$ log $P(x_i;\theta)$ = $\underset{p_1,...,p_d}{argmax}$ log $(\prod_{i=1}^n \prod_{k=1}^d p_k^{x_{i,k}})$
- 주어진 가능도 함수에다 log를 씌어주게 되면 로그연산의 성질에 의해서 곱셈을 아래와 같이 덧셈으로 바꿀 수 있다
- log $(\prod_{i=1}^n \prod_{k=1}^d p_k^{x_i,k}) =$ $\sum_{k=1}^d(\sum_{i=1}^n x_{i,k})$ log $p_k$
  - $n_k = \sum_{i=1}^n x_{i,k}$
    - $n_k$ : 주어진 데이터 $x_i$ 에 대해서 k 값이 1인 데이터의 갯수를 counting하는 개념
- therefore; log $(\prod_{i=1}^n \prod_{k=1}^d p_k^{x_i,k}) =$ $\sum_{k=1}^dn_k$ log $p_k$
- 카테고리 분포의 모수는 아래와 같은 제약식을 만족하면서 위에 목적식을 최대화하는 것이 우리가 구하는 MLE이다
  - $\sum_{k=1}^d p_k = 1$
    - 카테고리 분포의 모수 $p_1,...,p_d$ 는 1에서부터 d차원까지 각각의 차원에서 값이 1또는 0이 될 확률을 의미하는 모수이다
라그랑주 승수법을 통해 최적화(제약식을 만족함과 동시에 로그 가능도를 최대화시키는) 문제를 풀 수 있다
- $\mathcal{L}(p_1,...,p_k,\lambda) = \sum_{k=1}^d n_k$ log $p_k + \lambda(1- \sum_k p_k)$
- 주어진 라그랑주 목적식을 각각의 모수 $p_k$ 에 대해서 미분을 해준다음 라그랑주에 승수인 람다에 대해서 미분을 한다

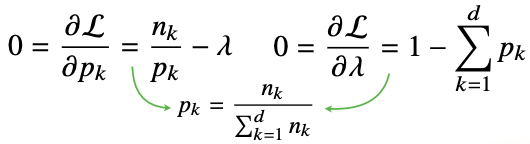
분모에 해당되는 $\sum_{k=1}^d n_k$ 는 데이터 갯수인 n이랑 같다
- 그렇기 때문에 $p_k =$ $n_k \over n$ 이는 카테고리 분포의 MLE는 각각의 차원에 해당하는 데이터의 경우의 숫자를 세어서 비율을 구하는 것이다

딥러닝에서 최대가능도 추정법

최대가능도 추정법을 이용해서 기계학습 모델을 학습할 수 있다
딥러닝 모델의 가중치를 $\theta = (W^{(1)},...,W^{(L)})$ 라 표기했을 때 분류 문제에서 소프트맥스 벡터는 카테고리분포의 모수 $(p_1,...,p_k)$ 를 모델링 한다
원핫벡터로 표현한 정답레이블 y = $(y_1,...,y_k)$ 을 관찰데이터로 이용해 확률분포인 소프트맥스 벡터의 로그가능도를 최적화해서 딥러닝의 모수인 $\theta$ 를 학습시킬 수 있다
- $\hat{\theta}_{MLE} = \underset{\theta}{argmax}$ $1 \over n$ $\sum_{i=1}^n \sum_{k=1}^K y_i,k$ log ( $MLP_{\theta}(x_i)_k)$
- 모든 클래스 k에 대해서 모든 데이터 n에 대해 multi layer perceptron의 예측값의 k번째 예측값의 로그값과 정답레이블에 해당하는 $y_k$ 번째 주소값을 곱해준것들의 덧셈으로 표현해준다

확률분포의 거리를 구해보자

기계학습에서 사용되는 손실함수들은 모델이 학습하는 확률분포와 데이터에서 관찰되는 확률분포의 거리를 통해 유도한다
데이터공간에 두 개의 확률분포 $P(\mathrm{x}), Q(\mathrm{x})$ ㅏ 있을 경우 두 확률분포 사이의 거리 (distance) 를 계산할 때 다음과 같은 함수들을 이용한다
- 총변동 거리 (Total Variation Distance, TV)
- 쿨백-라이블러 발산 (Kullback-Leibler Divergence, KL)
- 바슈타인 거리 (Wasserstein Distance)

쿨백-라이블러 발산

KL Divergence 는 다음과 같이 정의한다
- 이산확률변수 :
  $\mathbb{KL}(P||Q) = \sum_{\mathrm{x} \in \mathcal{X}} P(\mathrm{x})$ log $P(\mathrm{x}) \over Q(\mathrm{x})$
- 연속확률변수 :
  $\mathbb{KL}(P||Q) = \int_{\mathcal{X}} P(\mathrm{x})$ log $P(\mathrm{x}) \over Q(\mathrm{x})$ $\mathrm{dx}$
쿨백 라이블러는 다음과 같이 분해할 수 있다
- $\mathbb{KL}(P||Q) = -\mathbb{E}_{\mathrm{x}\sim P(\mathrm{x})}[log Q(\mathrm{x})]$ + $\mathbb{E}_{\mathrm{x}\sim P(\mathrm{x})}[log P(\mathrm{x})]$
  - $-\mathbb{E}_{\mathrm{x}\sim P(\mathrm{x})}[log Q(\mathrm{x})]$ : 크로스 엔트로피
  - $\mathbb{E}_{\mathrm{x}\sim P(\mathrm{x})}[log P(\mathrm{x})]$ : 엔트로피
분류 문제에서 정답레이블을 $P$ , 모델 예측을 $Q$ 라 두면 최대가능도 추정법은 쿨백-라이블러 발산을 최소화 하는 것과 같다
- 최대가능도 추정법에서 로그가능도를 최대화 시키는 것은 정답레이블에 해당하는 확률분포 P와 모델예측에서 사용되는 확률분포 Q 거리(쿨백 라이블러 발산)를 최소화하는 것과 동일하다
- 확률분포 사이의 거리를 최소화하는 개념과 가능도함수를 최대화 시키는 개념이 밀접하게 연결되있다

Andrew

아기개발자

이전 포스트

Pandas (cont.) / 확률론

다음 포스트