딥러닝 기초

Andrew·2021년 2월 1일

[Contents]

1) 베이즈 통계학 맛보기
2) 뉴럴 네트워크 - MLP
3) 데이터셋 다루기

베이즈 통계학 맛보기

조건부확률에서 이어지는 개념인 베이즈 정리와 인과관계 추론에 대해 설명

베이즈 정리는 데이터가 새로 추가되었을 때 정보를 업데이트하는 방식에 대한 기반이 되므로 오늘날 머신러닝에 사용되는 예측모형의 방법론으로 굉장히 많이 사용되는 개념

이 때 나오는 사전확률, 사후확률, evidence 등의 개념은 강의에서 나오는 예제를 활용해서 정확히 이해해야한다

인과관계 추론의 경우, 조건부확률을 섣불리 사용해선 안되는 이유와 중첩효과를 제거함으로써 얻은 인과관계를 어떤 방식으로 활용할수 있는지에 초점을 두고 공부하자

조건부 확률이란?

베이즈 통계학을 이해하기 위해선 조건부확률의 개념을 이해해야 한다
- $P(A \cap B)$ = $P(B)P(A|B)$
  - 조건부확률 $P(A|B)$ 는 사건 B가 일어난 상황에서 사건 A가 발생할 확률을 의미한다
베이즈 정리는 조건부확률을 이용하여 정보를 갱신하는 방법 을 알려준다
- $P(B|A)$ = $P(A \cap B) \over P(A)$ = $P(B)$ $P(A|B) \over P(A)$
  - A 라는 새로운 정보가 주어졌을 때 $P(B)$ 로 부터 $P(B|A)$ 를 계산하는 방법을 제공

베이즈 정리 : 예제

$\theta$ : hypothesis, 모델링하는 어떤 이벤트, 모델에서 계산하고 싶은 parameter(모수)
$\mathcal{D}$ : 새로 관찰하는 데이터
사후확률 : 데이터를 관찰 했을때 이 hypothesis가 성립할 확률, 데이터를 관찰한 이후에 측정을 하는 확률이기 때문에 사후확률이라 부른다
사전확률 : 데이터가 주어지지 않은 상황에서 $\theta$ 에 대한 모델링을 하기 이전에 주어진 확률, 데이터를 분석하기 전에 어떤 hypothesis(모델링 하고자 하는 target) 에 대해서 사전에 가정
가능도(likelihood) : 현재 주어진 hypothesis(모수 또는 parameter) 에서 이 데이터가 관찰될 확률
evidence : 데이터 자체의 분포
COVID - 99 의 발병률이 10% 로 알려져있다. COVID - 99 에 실제로 걸렸을 때 검진될 확률은 99%, 실제로 걸리지 않았을 때 오검진될 확률이 10% 라고 할 때, 어떤 사람이 질병에 걸렸다고 검진결과가 나왔을 때 정말로 COVID - 99 에 감염되었을 확률 은?
- 사전확률, 민감도(recall), 오탐률(false alarm)을 가지고 정밀도(precision)를 계산하는 문제이다
- $\theta$ 를 COVID - 99 발병 사건으로 정의(관찰 불가)하고, $\mathcal{D}$ 를 테스트 결과라고 정의(관찰가능) 한다.
  - 사전확률 $P(\theta)$ = 0.1,
  - 가능도 $P(\mathcal{D}|\theta)$ = 0.99
  - 가능도 $P(\mathcal{D}|ㄱ\theta)$ = 0.1 # ㄱ = $\theta$ 를 부정하는 수식( $\theta$ 의 negation 즉, $\theta$ 가 아닌 상황에서 $\mathcal{D}$ 가 관찰될 확률)
  - $P(\mathcal{D})$ = $\sum_{\theta} P(\mathcal{D}|\theta)P(\theta)$ = 0.99 x 0.1 + 0.1 x 0.9( $P(ㄱ\theta)$ ) = 0.189
    - 만일 $P(\mathcal{D}|ㄱ\theta)$ 를 모른다면 이 문제는 풀기 어렵다
  - $P(\theta|\mathcal{D})$ = 0.1 x $0.99 \over 0.189$ $\approx$ 0.524

조건부 확률의 시각화

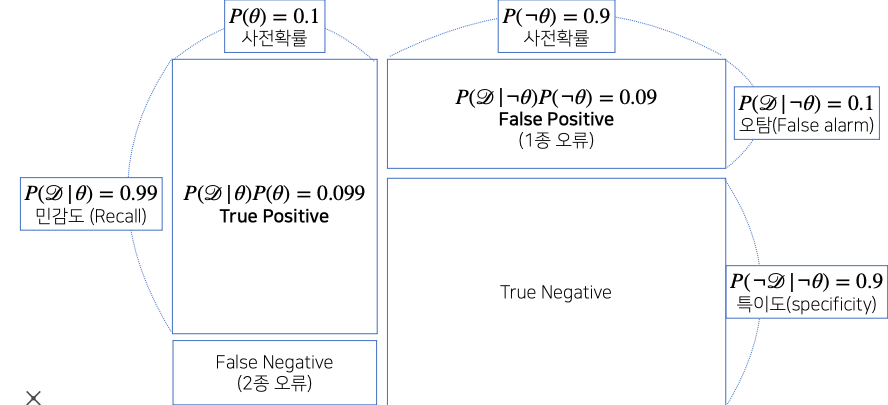
2종 오류 같은 경우는 질병이 아니라 라고 판정을 한 상황에서 실제로 질병일 경우를 말하는 오류기 때문에 False Negative(2종 오류) 같은 경우는 실제 의료 문제에서 많이 신경 쓰는 matrix 이다
1종 오류는 상대적으로 심각도가 좀 더 떨어진다 그렇기 때문에 False Positive를 희생하더라도 False Negative 를 줄이는 형식으로 테스트를 설계한다
민감도 : 질병에 실제로 걸렸을때 데이터가 관찰될 확률
사전확률(recall) : 실제 이 질병의 발생률
- 데이터 분석을 하기 전에 사전에 주어진 정보, 사전확률 없이는 베이즈 통계학에서 분석을 하긴 어렵다
- 만약 사전확률을 모르는 경우에는 임의로 사전확률을 설정하는 경우도 있으나 이 경우에는 베이즈 통계학에서 분석의 신뢰도가 떨어진다
만약에 오탐률(False alarm) 을 줄이게 되면 분모에 들어가는 FP 가 줄어들기 때문에 정밀도 계산이 높아진다

베이즈 정리를 통한 정보의 갱신

베이즈 정리를 통해 새로운 데이터가 들어왔을 때 앞서 계산한 사후확률을 사전확률로 사용하여 갱신된 사후확률을 계산 할 수 있다
- 데이터가 새로 들어왔을때 베이즈 정리를 통해 정보를 갱신하는 것이 가능하다

이 프로세스의 반복을 통해서 데이터를 새로 관찰할 때마다 hypothesis 또는 모델의 parameter $\theta$ 를 점점 업데이트 하는 형태로 모델의 정확도/예측력을 향상 시킬 수 있다
앞서 COVID - 99 판정을 받은 사람이 두 번째 검진을 받았을 때도 양성이 나왔을 때 진짜 COVID-99에 걸렸을 확률은?

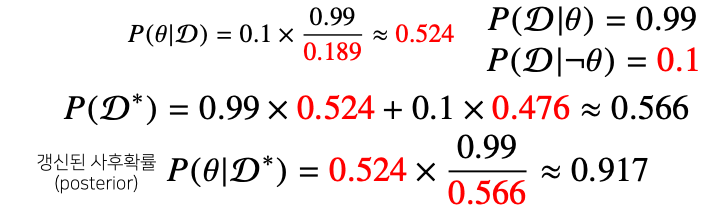
세번째 검사해도 양성이 나오면 정밀도가 99.1% 까지 갱신된다
즉, 베이즈 통계의 장점은 데이터가 새로 들어올 때마다 사후확률을 업데이트 할 수 있다
업데이트된 사후확률을 가지고 모델링이 가능하기 때문에 실제로 유효한 테스팅이 가능하다

조건부 확률 -> 인과관계?

조건부 확률을 유용한 통계적 해석을 제공하지만 인과관계(causality) 를 추론할 때 함부로 사용해서는 안된다
- 인과관계 : 실제 두 개의 사건(A, B)이 있을때 A 가 B의 원인인가?
- 데이터가 많아져도 조건부 확률만 가지고 인과관계를 추론하는 것은 불가능하다
인과관계는 데이터 분포의 변화에 강건한 예측모형 을 만들 때 필요하다

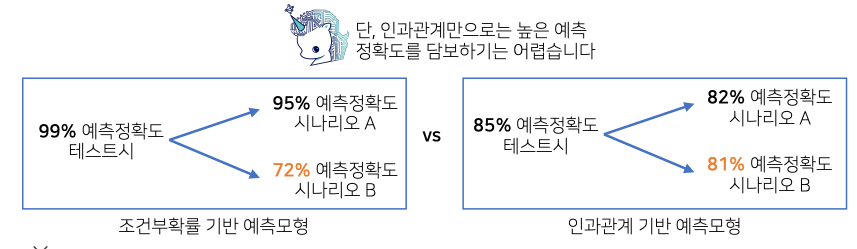
좌측 : 인과관계를 고려하지 않고 조건부확률 기반 예측모형 (실제 테스트시 높은 정확도)
- 데이터 분포가 바뀌게 되는 경우에 즉, 데이터가 유입되는 상황이 바뀌거나 또는 새로운 정책을 도입했을때 또는 새로운 치료법을 도입했을때 유입되는 데이터 분포가 변화는 경우에는 조건부 확률만 가지고 예측만 만들었을때 시나리오에 따라 예측 확률이 크게 변할수 있다
우측 : 인과관계 기관 예측모형
- 인과관계만 고려해서 예측모형을 만들게 되면 높은 예측 정확도를 담보하는 것은 어렵다
- 다만 데이터 분포의 변화에 강건한 예측모형을 만들수 있기 때문에 여러 시나리오가 발생했을때도 예측 정확도가 크게 변하지 않는 상황을 보장하는 것이 가능하다
인과관계를 알아내기 위해서는 중첩요인(confounding factor, Z)의 효과를 제거 하고 원인에 해당하는 변수만의 인과관계를 계산해야 한다

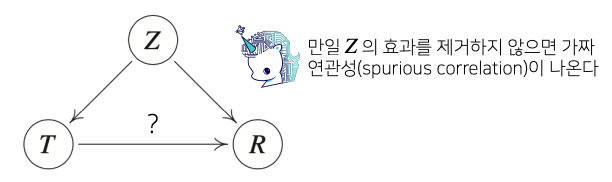
Z를 제거해야만 T를 원인으로 했을때 결과에 해당하는 R에 인과관계를 계산할 수 있다
- 원인과 결과에 해당하는 인과관계(위 그림에서 ?)를 계산할 때는 Z가 T랑 R에 둘다 영향을 주기 때문에 Z의 중첩적인 효과를 제거하지 않으면 spurious correlation을 불러온다
- 이게 바로 예측모형에서 데이터 분포에 변화가 생겼을때 예측 모델의 정확도를 떨어트리는 가장 큰 요인이 될 수 있다
- 에제1) R : 지능지수, T : 키
  - 키가 크냐 작냐에 따라서 지능지수가 높냐 낮냐는 모델을 데이터 분석을 했을때 보통 일반적으로는 키와 지능은 별로 관계가 없을것 처럼 보이는데
  - 하지만 키가 클수록 지능지수가 높다는 분석이 나온다
  - 그 이유는 연령(나이) 라는 중첩효과를 제거하지 않아서 이다
  - 당연히 나이가 들면 들수록 키가 큰다 또한 나이가 들수록 지능지수도 높아진다
  - 이게 중첩요인이 되어서 마치 키가 크면 지능지수가 높다라는 식의 데이터 분석을 할 수 있다
- 예제2)
  - 커피를 마시는 사람들이 암발병률이 높은데 이는 커피 때문이 아니라 커피를 마시는 사람들이 담배를 피우는 경향이 높기 때문이다
  - 따라서 담배 피는지 여부를 포함해서 분석해야 올바른 결론이 나온다
  - 즉, 중첩요인(Confounding factor)을 모형에 포함시켜서 보정해주어야 인과관계에 대해 보다 정확한 결론을 얻을수 있는데,
  - 문제는 현실적으로 중첩요인을 모두 관측하지 못한다는 것이다
  - 따라서, 중요한 중첩요인을 빼놓고 분석을 하면 잘못된 결론을 얻는다

인과관계 추론 : 예제

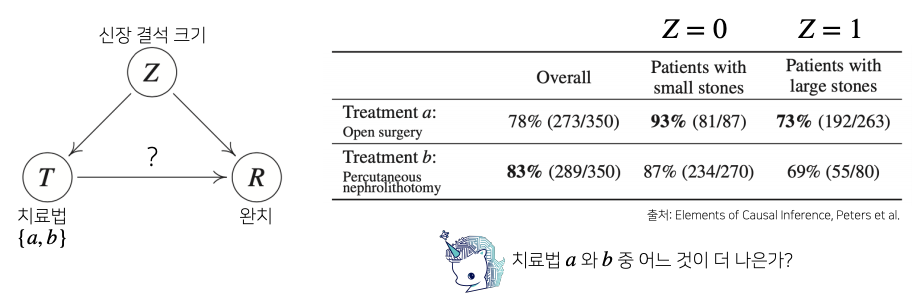
신장결석에 따라서 치료법 a(개복수술)와 b(주사 치료) 를 통해서 어떤 치료법이 완치율이 더 높은지에 대한 분석 즉, 치료법에 따른 완치율에 원인과 결과의 분석
전체적으로 봤을때는 치료법 b가 높은 완치율을 가진다
하지만 각각의 환자 군에 따라서 보게 되면 신장결석이 작을때나 클때도 치료법 a가 높다
이 역설 문제를 해결하기 위해서는 조건부확률만 계산해서는 안되고 신장결석 크기에 따른 치료법 a와b의 중첩효과를 제거해야만 실제 정확한 치료법에 따른 완치율을 계산하는 것이 가능하다
모든 환자가 신장결석 크기와 상관없이(중첩효과 제거) 치료법 a를 선택했을때의 완치율:

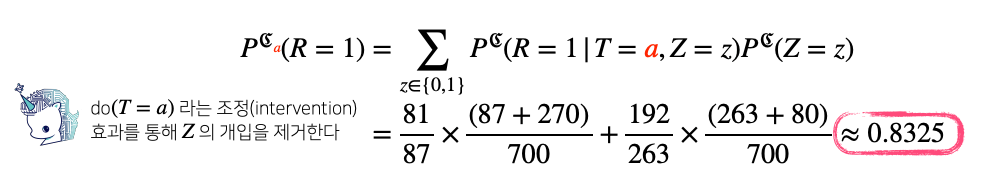
모든 환자가 신장결석 크기와 상관없이(중첩효과 제거) 치료법 b를 선택했을때의 완치율:

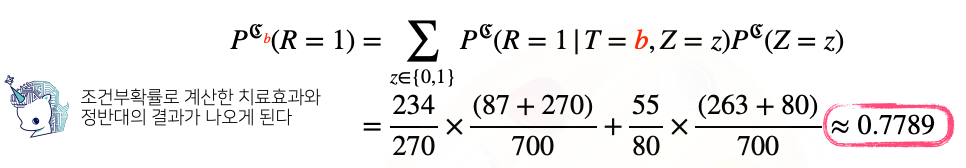
정리 :

단순히 조건부확률 데이터 분석을 하는 것은 상당히 위험하다

데이터에서 추론할 수 있는 사실 관계, 데이터가 생성되는 관계들 또는 domain 지식을 활용을 해서 변수들 끼리의 관계를 파악해야만 인과관계 추론이 가능하다

강건한 데이터 모형을 만들기 위해선 데이터 분석시 인과관계도 고려해야한다

뉴럴 네트워크 - MLP

신경망(Neural Networks)의 정의, Deep Neural Networks에 대해 배운다

간단한 Linear neural networks를 예시로 Data, Model, Loss, Optimization algorithm을 정의해본다

Deep Neural Networks란 무엇이며 Multi-layer perceptron과 같이 더 깊은 네트워크는 어떻게 구성하는지에 대해 배운다

끝으로 Pytorch를 이용하여 MLP 실습

Further Questions

regression task, classification task, probabilistic task의 loss 함수(or 클래스)는 pytorch 에서 어떻게 구현이 되어있을까?

backpropagation

목표 : loss function을 줄인다
- parameter가 어느 방향으로 움직였을때 loss function 이 줄어드는지를 찾고 그 방향으로 parameter를 바꾸는것이 목표
- loss를 줄이는 것이 목표이기 때문에 loss function을 각각 parameter로 미분하게 되는 방향을 역수방향으로(그 방향에 음수 방향으로) parameter를 업데이트 하여 결국엔 loss가 최소화되는 지점(optimal parameter)을 찾는다

beyond linear neural networks

we need nonlinearity
- x란 입력에서 y를 출력하는 mapping이 표현할 수 있는 capacity
- 즉, 이 네트워크가 표현할 수 있는 표현력을 최대한 극대화 하기 위해서는 단순히 선형 결합을 n번 반복하는 것이 아니라
- 한번 선형 결합이 이루어진 뒤에 activation function(sigmoid, relu, hyperbolic tangent)을 곱해줘서 non-linear transform 을 거치고
- 이를 통해 얻어 지는 feature vector를 다시 선형변화 하고 non-linear transformation 을 거치는 과정을 n번 반복하게 되면 더 많은 표현력을 갖게 된다
loss function
- loss function이 어떤 성질을 가지고 있고 이게 왜 내가 원하는 결과를 얻어낼 수 있는지를 바탕으로 모델의 목적성에 맞춰서 loss function을 사용해야 한다