그래프 신경망이란 무엇일까? (기본)
- 대표적인 귀납식 embedding 방법이다
- 이번에는 정점 표현 학습(Node Representation Learning)의 방법 중 한 가지인 그래프 신경망(Graph Neural Network, GNN)에 대해서 배운다
- 최근 딥러닝에서 촉망 받고 있는 그래프 신경망, 과연 무엇을 학습시키는 것이고 어떤 방식으로 학습이 이루어질까? 그리고, 이전에 나온 합성곱 신경망(Convolutional Neural Network)과 어떤 점이 다른 것일까? 그냥 합성곱 신경망을 사용하면 안될까?
- 위와 같은 질문들에 대한 답변을 할 수 있다면, 누군가가 그래프 신경망에 대해 질문하여도 멋지게 대답할 수 있지않을까? :)
Further Reading
귀납식 임베딩 방법의 장점
- 출력으로 인코더를 얻는 귀납식 임베딩 방법 은 여러 장점을 갖는다
- 학습이 진행된 이후에 추가된 정점에 대해서도 임베딩을 얻을 수 있다
- 모든 정점에 대한 임베딩을 미리 계산하여 저장해둘 필요가 없다
- 그때 그때 필요한 정점에 대해서 함수를 적용해서 벡터를 얻어낼 수 있다
- 정점이 속성(Attribute) 정보를 가진 경우에 이를 활용할 수 있다
- 인코더 함수를 디자인 할 때 이 함수가 입력으로 속성 정보까지 활용할 수 있도록 함수의 구조를 설계한다

- 인코더 함수를 디자인 할 때 이 함수가 입력으로 속성 정보까지 활용할 수 있도록 함수의 구조를 설계한다
그래프 신경망 기본
그래프 신경망의 구조
- 그래프 신경망은 그래프 와 정점의 속성 정보 를 입력으로 받는다
- 그래프의 인접 행렬을 라고 하자
- 인접 행렬 은 의 이진 행렬이다
- 각 정점 의 속성(Attribute) 벡터 를 라고 하자
- 정점 속성 벡터 는 차원 벡터이고, 은 속성의 수를 의미한다
- 정점의 속성 의 예시는 다음과 같다
- 온라인 소셜 네트워크에서 사용자의 지역, 성별, 연령, 프로필 사진 등
- 논문 인용 그래프에서 논문에 사용된 키워드에 대한 원-핫 벡터
- PageRank 등의 정점 중심성, 정점 별로 계산한 지역적 군집 계수(Clustering Coefficient) 등
- 이렇듯 속성은 데이터로 주어질 수도 있고 그래프를 분석해서 얻어낼 수도 있다
- 그래프 신경망은 이웃 정점들의 정보를 집계하는 과정을 반복 하여 대상 정점의 임베딩(최종 output) 을 얻는다
- 예시에서 대상 정점 의 임베딩을 얻기 위해 이웃들 그리고 이웃의 이웃들의 정보 를 집계한다
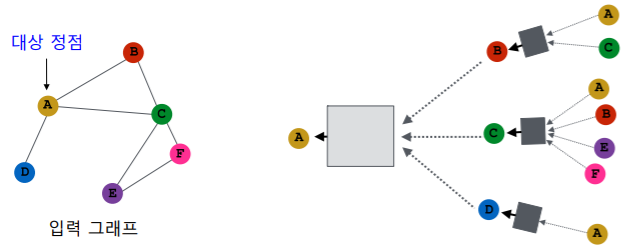
- 각 집계 단계를 층(Layer) 이라고 부르고, 각 층마다 임베딩 을 얻는다
- 각 층에서는 이웃들의 이전 층 임베딩을 집계하여 새로운 임베딩을 얻는다
- 0번 층, 즉 입력 층의 임베딩으로는 정점의 속성 벡터 를 사용한다
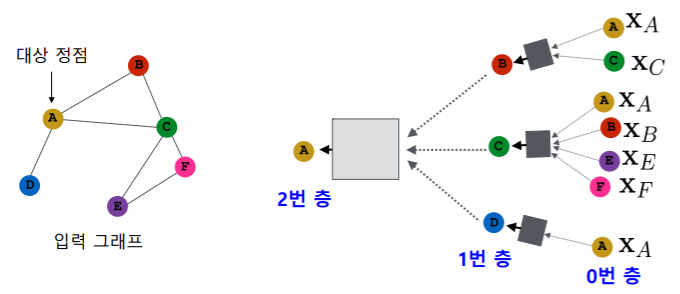
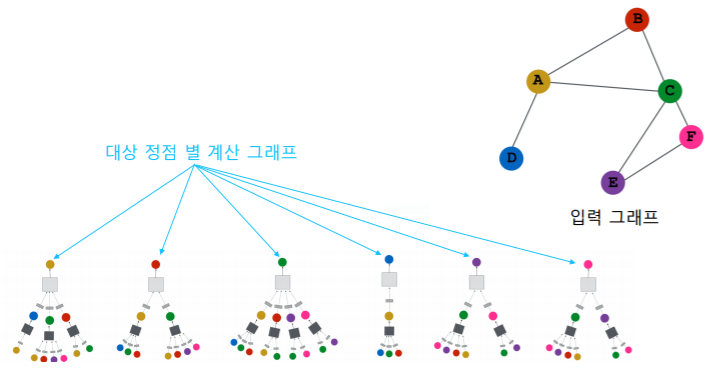
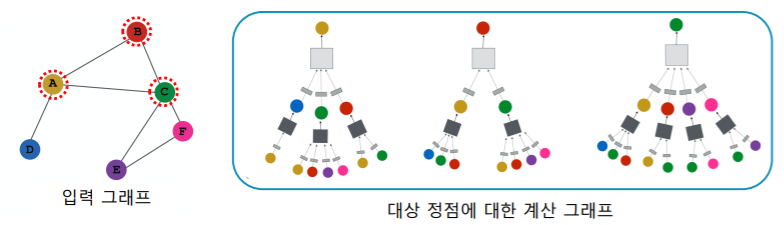
- 대상 정점 마다 집계되는 정보가 상이한다
- embedding을 얻고자 하는 정점이 무엇이냐에 따라서 집계되는 정보의 양과 정보 내용이 상이한다
- 대상 정점 별 집계되는 구조를 계산 그래프(Computation Graph) 라고 부른다
- 서로 다른 대상 정점간에도 층 별 집계 함수는 공유 한다
- 반면 서로 다른 층에서는 서로 다른 집계함수를 사용한다
- 입력의 크기가 가변적이여도 처리할 수 있는 형태이어야 한다
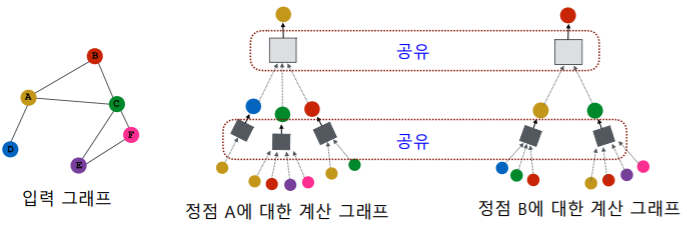
- 서로 다른 구조(입력이 가변적인 구조)의 계산 그래프를 처리하기 위해서는 어떤 형태의 집계 함수 가 필요할까?
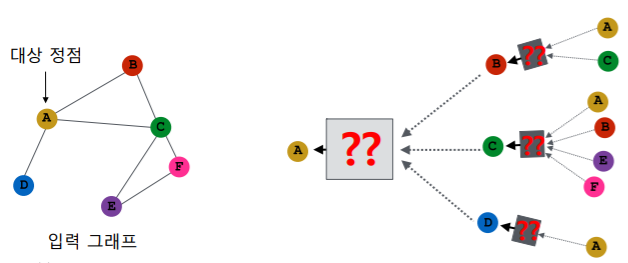
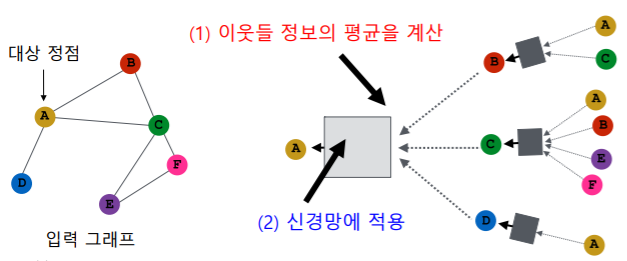
- 집계 함수는 (1) 이웃들 정보의 평균을 계산 하고 (2) 신경망에 적용 하는 단계를 거친다
- 평균을 내면 입력데이터의 갯수와 상관없이 평균 하나로 그 차원이 동일하게 축소된다
- 즉, 평균을 통해서 입력의 차원을 동일하게 만든 뒤 동일 차원에 데이터에 대해서 신경망을 적용한다
- 평균을 내면 입력데이터의 갯수와 상관없이 평균 하나로 그 차원이 동일하게 축소된다
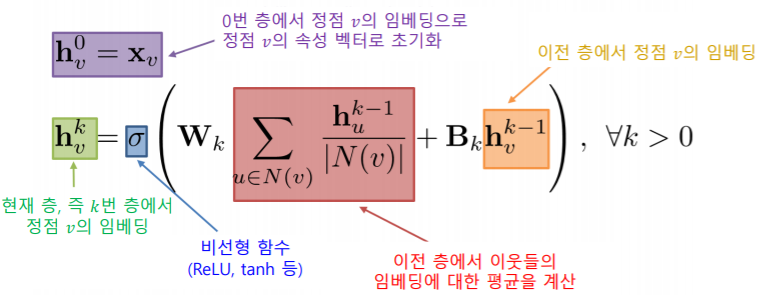
- : 정점 의 이웃들
- : 신경망을 통과 시키는 가중치
- : 이전 층에서의 자기자신의 정보
- 마지막 층에서의 정점 별 임베딩 이 해당 정점의 출력 임베딩 이다

- : 층의 수 (# of layers)
- : 층의 수 (# of layers)
그래프 신경망의 학습
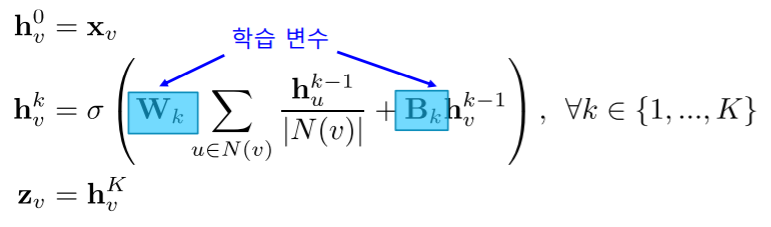
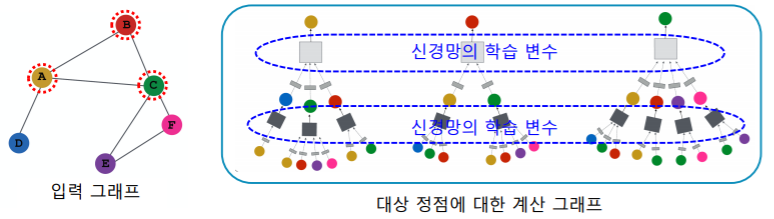
- 그래프 신경망의 학습 변수(Trainable Parameter) 는 층 별 신경망의 가중치 이다
- 정점 별 embedding 들도 물론 학습이 진행됨에 따라서 값이 바뀐다. 하지만 이것을 직접 바꾼다라고 하기 보다는
- 직접 바꾼 층 별 신경망의 가중치의 결과로 정점 별 embedding 값들이 바뀐다고 생각하자
- 정점 별 embedding 들도 물론 학습이 진행됨에 따라서 값이 바뀐다. 하지만 이것을 직접 바꾼다라고 하기 보다는
-
먼저 손실함수 를 결정한다
- 정점간 거리를 “보존” 하는 것을 목표로 할 수 있다
- 정점간 거리를 보존 하는 것도 그래프에서의 정점간 거리를 어떻게 정의하냐에 따라서 여러가지 손실함수가 있을 수 있다
- 변환식 정점 임베딩에서처럼 그래프에서의 정점간 거리를 “보존” 하는 것을 목표로 할 수 있다
- 만약, 인접성을 기반으로 유사도 를 정의한다면, 손실 함수 는 다음과 같다
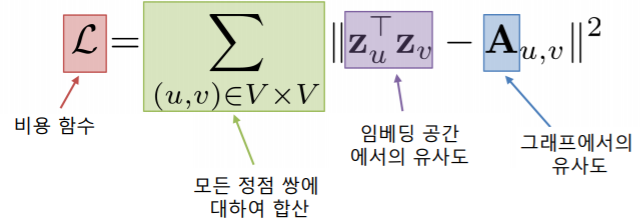
- : 그래프 신경망의 결과로 얻은 출력 embedding
- 정점간 거리를 “보존” 하는 것을 목표로 할 수 있다
-
후속 과제(Downstream Task)의 손실함수를 이용한 종단종(End-to-End) 학습 도 가능하다
- 정점 분류 가 최종 목표인 경우를 생각해보자
- embedding을 얻지만 embedding을 얻는것 자체가 목표가 아닌 이 embedding을 classifier에 통과시켜서 정점을 분류하는 목표
- 이런 경우에는 벡터의 embedding이 그래프에서의 유사도를 보존하냐 보존하지 않냐는 직접적인 관심이 아니다
- 우리의 관심은 이 embedding 벡터를 사용해서 분류기를 통과시켰을때 정확도가 얼마나 높은지 즉, 이 정확도를 올리는것이 우리의 직접적인 목표다
- 이런 직접적인 목표를 달성하기 위해서는 그 직접적인 목표와 더욱 관련된 손실함수를 사용해야 한다
- 예를 들어,
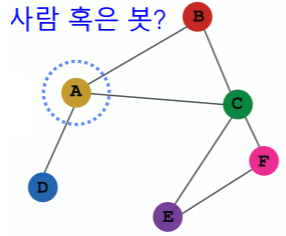
- 그래프 신경망을 이용하여 정점의 임베딩을 얻고
- 이를 분류기(Classifier)의 입력으로 사용하여
- 각 정점의 유형을 분류하려고 한다
- 이 경우 분류기의 손실함수, 예를 들어 교차 엔트로피(Cross Entropy) 를, 전체 프로세스의 손실함수로 사용하여 종단종(End-to-End) 학습 을 할 수 있다
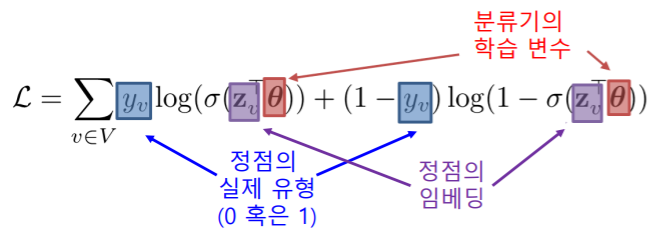
- , : 각 유형별 확률값
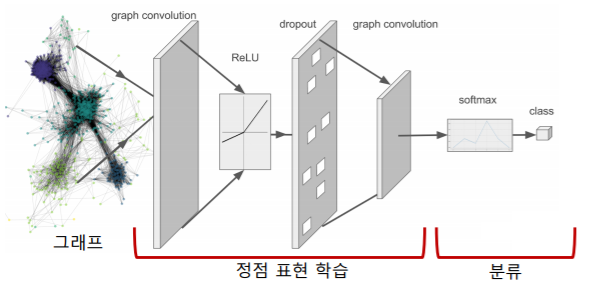
- 아래 그림에서 역전파를 단순히 classifier에만 하는것이 아니라 그래프 신경망까지 해서 학습을 진행한다
- 정점 분류 가 최종 목표인 경우를 생각해보자
- 그래프 신경망은 비지도 학습, 지도 학습 이 모두 가능하다
- 비지도 학습에서는 정점간 거리를 '보존' 하는 것을 목표로 한다
- 지도 학습에서는 후속 과제의 손실함수를 이용해 종단종 학습을 한다
- 그래프 신경망과 변환적 정점 임베딩을 이용한 정점 분류
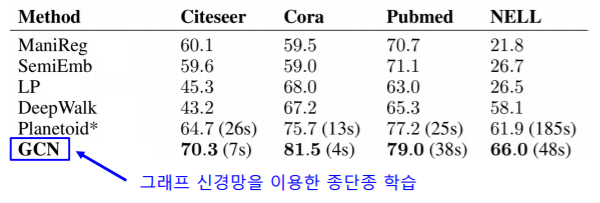
- 그래프 신경망의 종단종(End-to-End) 학습을 통한 분류 는, 변환적 정점 임베딩 이후에 별도의 분류기를 학습하는 것 보다 정확도가 대체로 높다
- 아래 표는 다양한 데이터에서의 정점 분류의 정확도(Accuracy)를 보여
- 학습에 사용할 대상 정점을 결정하여 학습 데이터를 구성한다
- 선택된 일부 대상 정점에 똑같은 집계함수를 공유해서 사용하기 때문에 일부 정점을 가지고 집계함수를 학습하고 이것을 다른 정점에도 그대로 적용할 수 있다
- 선택한 대상 정점들에 대한 계산 그래프를 구성한다
- 마지막으로 오차역전파(Backpropagation) 을 통해 손실함수를 최소화한다
- 구체적으로, 오차역전파 를 통해 신경망의 학습 변수 들을 학습한다
그래프 신경망의 활용
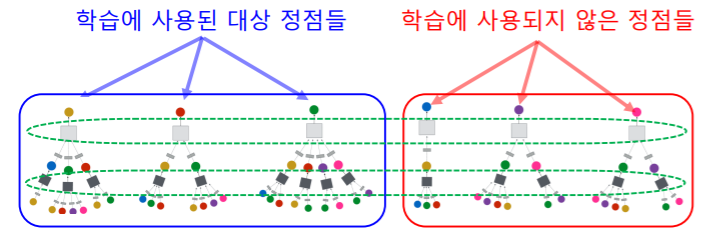
- 학습된 신경망을 적용하여, 학습에 사용되지 않은 정점의 임베딩 을 얻을 수 있다
- 일부 정점에 대해서 집계함수의 신경망 가중치들을 학습하고 나면 똑같은 집계함수를 활용하여서 학습에 사용되지 않은 대상 정점들의 embedding 또한 얻을 수 있다
- 학습된 신경망을 적용하여, 학습에 사용되지 않은 정점, 학습 이후에 추가된 정점, 심지어 새로운 그래프의 정점 의 임베딩을 얻을 수 있다
- 마찬가지로, 학습 이후에 추가된 정점의 임베딩 도 얻을 수 있다
- 온라인 소셜네트워크 등 많은 실제 그래프들은 시간에 따라서 변화한다
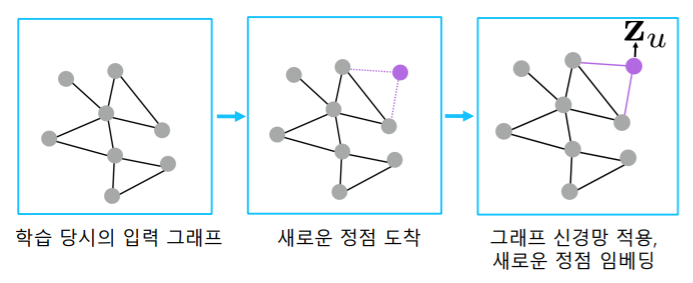
- 학습된 그래프 신경망을, 새로운 그래프에 적용 할 수도 있다
- 예를 들어, A종의 단백질 상호 작용 그래프에서 학습한 그래프 신경망을 B종의 단백질 상호작용 그래프에 적용할 수 있다
그래프 신경망 변형
그래프 합성곱 신경망
- 소개한 것 이외에도 다양한 형태의 집계 함수 를 사용할 수 있다
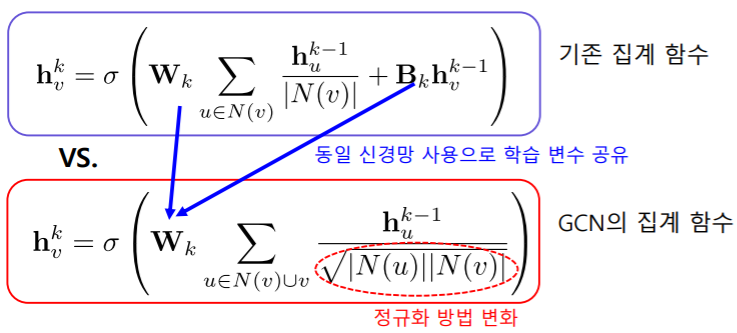
- 그래프 합성곱 신경망(Graph Convolutional Network, GCN) 의 집계 함수 이다
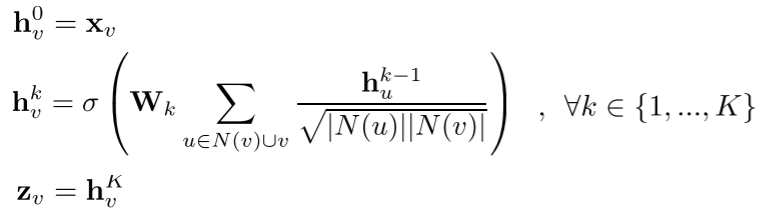
- 기존의 집계 함수와 비교봤을때 작은 차이지만 큰 성능의 향상으로 이어지기도 한다
- 가장 큰 차이점:
- 기존 집계 함수에서는 현재 집계가 되고 있는 정점의 이전 layer에서의 embedding을 별도의 라는 신경망을 이용하여 합계를 해줬는데
- GCN의 집계 함수에서는 기존에 신경망을 같이 사용해서 현재 집계 되고 있는 정점의 이전 layer 역시 함께 평균을 내는 것을 볼 수 있다
- 기존 집계 함수에서의 정규화 방법은 의 연결성만 사용을 했다면
- GCN 집계 함수에서는 의 연결성의 기하 평균을 사용하고 있다
- 가장 큰 차이점:
GraphSAGE
-
GraphSAGE 의 집계 함수 이다
- 이웃들의 임베딩을 AGG 함수 를 이용해 합친 후, 자신의 임베딩과 연결(Concatenation) 하는 점이 독특하다

- : 이웃들의 이전 layer의embedding을 받아오는 부분
- : 자기 자신의 이전 layer의 embedding
- 이웃들의 임베딩을 AGG 함수 를 이용해 합친 후, 자신의 임베딩과 연결(Concatenation) 하는 점이 독특하다
-
AGG 함수 로는 평균, 풀링, LSTM 등이 사용될 수 있다
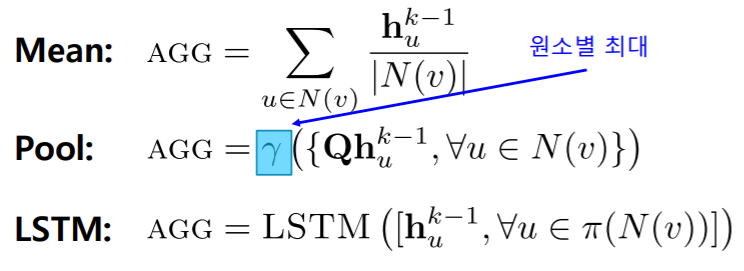
- : 이웃들의 embedding을 가져와서 순서를 섞은 다음에 LSTM에 넣어준다는 의미
합성곱 신경망과의 비교
합성곱 신경망과 그래프 신경망의 유사성
- 합성곱 신경망 과 그래프 신경망 은 모두 이웃의 정보를 집계하는 과정을 반복한다
- 구체적으로, 합성곱 신경망 은 이웃 픽셀의 정보를 집계하는 과정을 반복한다
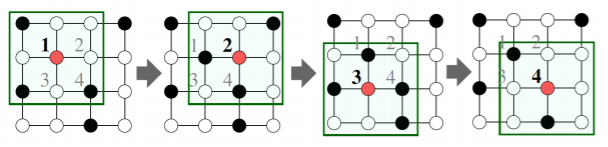
- 빨간색 대상 픽셀의 embedding을 얻기 위하여 대상 픽셀 주변에 있는 다른 8개의 픽셀과 본인 자기자신의 embedding을 집계한다
- 구체적으로, 합성곱 신경망 은 이웃 픽셀의 정보를 집계하는 과정을 반복한다
합성곱 신경망과 그래프 신경망의 차이
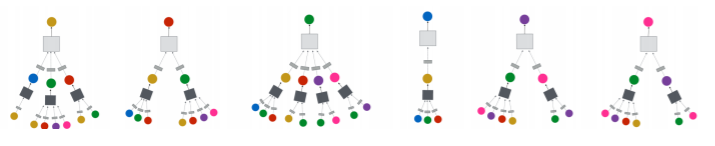
- 합성곱 신경망 에서는 이웃의 수가 균일하지만, 그래프 신경망 에서는 아니다
- 그래프 신경망 에서는 정점 별로 집계하는 이웃의 수가 다르다
- 그래프의 인접 행렬 에 합성곱 신경망 을 적용하면 효과적일까?
- 그래프에는 합성곱 신경망이 아닌 그래프 신경망(GNN) 혹은 GCN을 적용하여야 한다! 많은 분들이 흔히 범하는 실수다
- 합성곱 신경망이 주로 쓰이는 이미지에서는 인접 픽셀이 유용한 정보를 담고 있을 가능성이 높다
- 하지만, 그래프의 인접 행렬에서의 인접 원소는 제한된 정보를 가진다 특히나, 인접 행렬의 행과 열의 순서는 임의로 결정되는 경우가 많다
