Transformer II

Andrew·2021년 2월 18일

boostcamp

Transformer II

Transformer (Self-Attention)에 대해 이어서 자세히 알아보자

Further Question

Attention은 이름 그대로 어떤 단어의 정보를 얼마나 가져올 지 알려주는 직관적인 방법처럼 보입니다. Attention을 모델의 Output을 설명하는 데에 활용할 수 있을까요?
- 참고: Attention is not explanation
- 참고: Attention is not not explanation

Transformer: Multi-Head Attention

self-attention 모듈을 유연하게 확장한 multi-head attention
Problem of single attention
- Only one way for words to interact with one another
Solution
- Multi-head attention maps 𝑄,𝐾,𝑉 into the ℎ number of lower-dimensional spaces via 𝑊 matrices
- Then apply attention, then concatenate outputs and pipe through linear layer
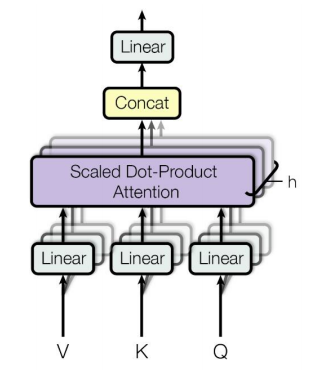
위 그림은 앞서 배운 attention 모듈을 나타낸다
h : 동시에 병렬적으로 여러버전의 attention을 수행한다
- $MultiHead(Q,K,V) = Concat(head_1, ..., head_h)W^O$
  - where $head_i = Attention(QW_i^Q, KW_i^K, VW_i^V)$
- 구체적으론 $W_Q, W_K, W_V$ 가 하나의 행렬 세트만 존재하는것이 아니라 여러 버전의 행렬들이 존재하고 즉 $i$ 번째의 attention 에서는 그 해당하는 $i$ 번째의 $W_Q, W_K, W_V$ 행렬을 써서 선형변환 후 attention 을 수행해서 각 query 벡터에대한 encoding(output) 벡터를 얻는다
- 서로다른 버전의 attention의 갯수만큼 동일한 query 벡터에 대한 서로다른 버전의 encoding(output) vector가 나오고 모든 encoding vector를 concat함으로써 그 해당 query 벡터에 대한 encoding 벡터를 최종적으로 얻게 된다
- 여러 버전의 attention을 수행하기 위함 선형 변환 matrix를 서로다른 head라 부른다
Multi-head attention이 필요한 이유:
- 어떤 동일한 sequence 가 주어졌을때도 특정한 query 단어에 대해서 서로 다른 기준으로 여러측면에서의 정보를 필요로할 수 있다
- 가령 여러 문장으로 이루어져 있는 'I went to school', 'I studied hard', 'I came back home and I took a rest'
- 이렇게 주어진 여러문장이 있을때 'I'라는 query 단어에 대한 encoding을 수행하기 위해서는 먼저 'I'라는 주체가 한 행동을 중심으로 즉, 'went', 'studied', 'came', 'took' 을 중심으로 정보를 뽑아올수 있게 되고
- 또 다른 측면에서는 'I'라는 주체가 존재하는 장소의 변화 가령 'school', 'home' 이런 장소에 해당하는 정보를 또 뽑을수가 있게 된다
- 이런 방식으로 서로 다른 측면의 정보를 병렬적으로 뽑고 그 정보들을 다 합치는 형태로 attention 모듈을 구성할 수 있다
  - 각각의 head가 이런 정보들을 상호 보완적으로 뽑는 역할을 하게된다
이를 도식화해서 나타내면:

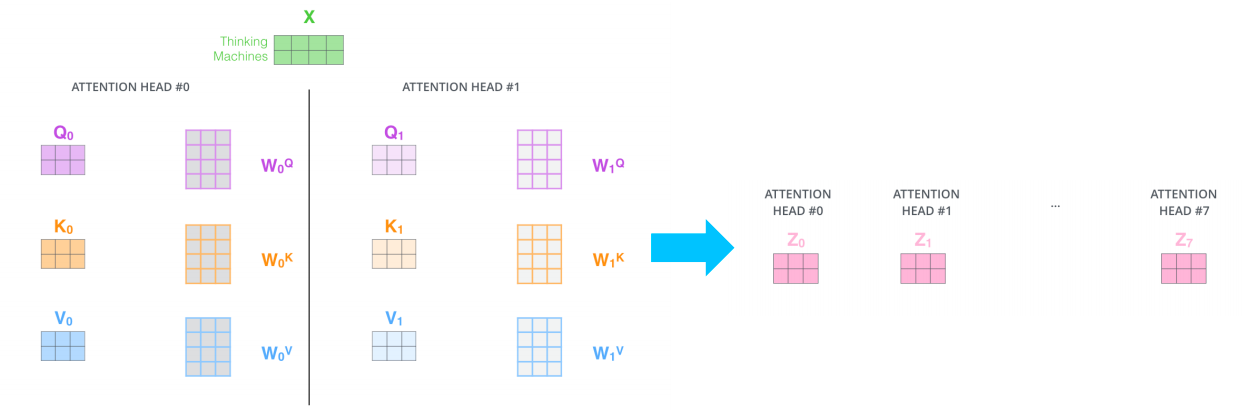
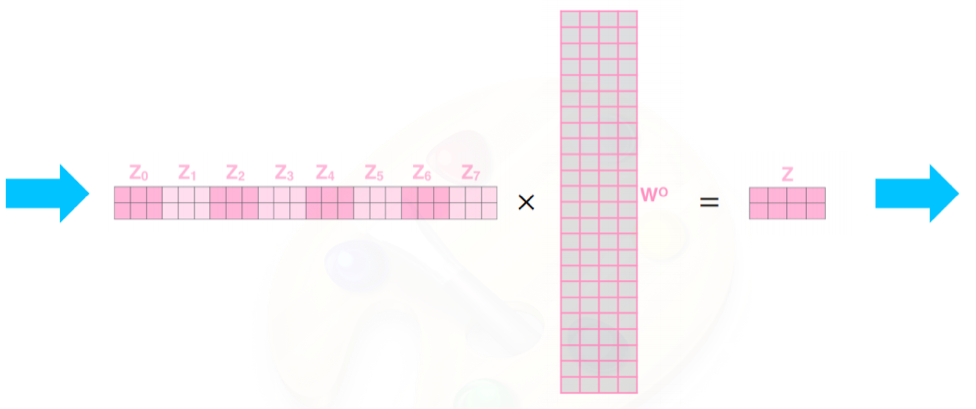
$W_O$ = 원하는 dimension으로 줄여주는 역할을 해주는 선형변환

위의 attention 모델의 계산량과 메모리 요구량의 특성을 살펴보고 기존의 RNN 기반의 sequence encoding 과 비교

maximum path lengths, per-layer complexity and minimun number of sequential operations for different layer types

$n$ is the sequence length
$d$ is the dimension of representation
$k$ is the kernel size of convolutions
$r$ is the size of the neighborhood in restricted self-attention

Layer Type	Complexity per Layer(메모리 요구량)	Sequential Operations(시간 복잡도)	Maximum Path Length
Self-Attention	$O(n^2 \cdot d)$	$O(1)$	$O(1)$
Recurrent	$O(n \cdot d^2)$	$O(n)$	$O(n)$
Convolutional	$O(k \cdot n \cdot d^2)$	$O(1)$	$O(log_k(n))$
Self-Attention(restricted)	$O(r \cdot n \cdot d)$	$O(1)$	$O(\frac{n}{r})$

Self-Attention $softmax(\frac{QK^T}{\sqrt{d_k}})V$ 연산에서 $QK^T$ 가 주된 계산을 차지한다
$n$ 개의 query와 $n$ 개의 key에 대한 $d$ dimension의 모든 가능한 페어에 대한 내적값을 계산해야한다
- $Q = (n \times d), K^T = (d \times n)$
- 즉, $(n \times d) \times (d \times n)$ 여기서는 특정한 query와 특정한 key에 대해서 $d$ dimension의 내적을 계산해야하고 $d$ dimension의 내적은 기본적으로 $d$ 만큼의 곱셈 및 덧셈을 수반하게되고 이것을 모든 query와 key에 대한 조합에 대해서 수행해줘야 하기때문에 $n^2 \times d$ 만큼의 계산이 가장 많은 부분 차지한다
- 그림으로 확인해보면:
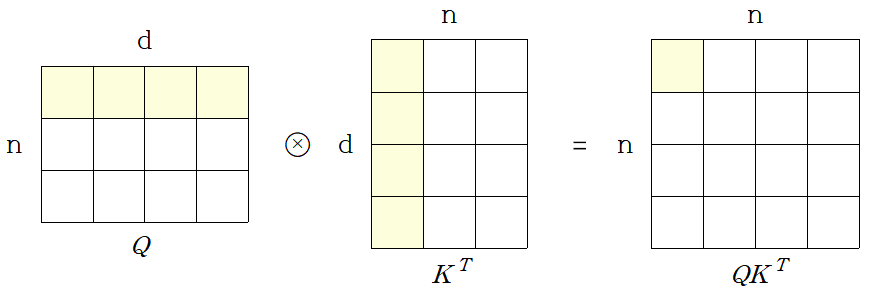
- 그렇지만 이러한 행렬 연산은 GPU의 코어수가 충분히 많다면 sequence가 아무리 길든 혹은 dimension 수가 아무리 크든 모든 계산을 GPU가 가장 특화된 행렬연산의 병렬화를 통해서 코어수가 무한정 많다는 전제하에 이것을 모두다 한번에 계산할 수 있다
그에 비해 Recurrent Neural Net(RNN)의 경우는 주로 필요한 계산량이 self-attention모델과는 달리 $O(n \cdot d^2)$ 와 같이 표현된다
- 이것은 각 time step 에서 계산되는 과정을 살펴볼때 $h_{t-1}$ 의 hidden state vector가 다음 time step의 hidden state vector에 변환이 되어서 참여할때 $h_{t-1}$ 의 dimension이 $d$ 라고 하면 vanilla RNN 구조에서 봤던거 처럼 $h_{t-1}$ 벡터의 $d$ dimension과 $W_{hh}$ 행렬의 $d$ dimension과 곱하여 $d$ dimension의 벡터를 출력한다
  - 그럴때 $h_{t-1}$ 행렬과 $W_{hh}$ 벡터의 곱을 할때는 각각의 $W_{hh}$ 의 row vector 와 $h_{t-1}$ 의 내적을 수행하는데 이 경우 총 $d$ 번의 계산이 필요하고 또한 각각의 $W_{hh}$ 상에서의 row vector 와 이 계산을 수행해야 하기 때문에 결국엔 $d^2$ 만큼의 계산량이 필요하게 된다
  - 이 계산을 매 time step 마다 순차적으로 수행해줘야 하기 때문에 time step 갯수인 $n$ 과 각 time step에서 일어나는 계산량 $d^2$ 만큼의 계산이 필요하게 된다
self-attention과 RNN의 메모리 요구량의 차이:
- $d$ 라는 값은 RNN이나 self-attention layer를 정의할때 사용자가 임의로 정할수 있는 hidden state vector의 dimension 으로써 hyper-parameter 가 된다
- $n$ 이라는 것은 입력 데이터의 sequence 가 길면 길수록 길어지는 값이기 때문에 임의로 길이를 고정된 값으로 사용할수 있는것이 아니라 주어진 입력에 따른 가변적인 값을 가지는 형태가 된다
- 그렇다면 self-attention에서는 좀 더 긴 sequence를 가지는 입력이 주어졌을때는 sequence길이의 제곱의 비례하는 계산량과 메모리 사이즈가 필요하게 된다
- RNN에서는 그에비해 sequence길이의 단지 1차 함수로써 비례하는 형태가 되기 때문에 일반적으로 self-attention에서는 RNN보다 훨씬 더 많은 메모리 요구량이 필요하게 된다
여러 계산들 중에 병렬화가 가능한 측면에서의 RNN과 self-attention 모델의 차일 살펴보자:
- self-attention은 sequence길이가 아무리 길더라도 GPU 코어수가 충분히 뒷받침 된다면 그 모든 계산을 동시에 수행할수 있다
- RNN의 경우는 $h_{t-1}$ 을 해야만 재귀적으로 다음 time step의 입력으로 넣어줄수 있기 때문에 $h_t$ 를 계산하기 위해서 $h_{t-1}$ 이 계산될때까지 기다릴수 밖에 없다, 즉 병렬화가 불가능하다
- 따라서 RNN의 forward와 backpropagation에서는 sequence 길이에 비례하는(병렬화가 불가능한) sequential 한 operation이 필요로 한다 ( $O(n)$ )
- 이러한 사실 때문에 일반적으로 self-attention기반의 transformer모델은 학습은 훨씬 더 RNN보다 빨리 진행될수 있지만 더 많은 양의 메모리를 필요로 한다
long-term dependency 와 직접적으로 관련된 Maximum path length 관에 살펴보자:
- sequence gap이 차이가 클 때 RNN의 경우는 RNN의 layer를 time step의 차이 만큼 지나가야한다 즉, path length는 최대 길이가 $n$ 인 sequence에 대해서 $O(n)$ 가 된다
- self-attention에서는 가장 끝에 있는 단어라 하더라도 가장 처음에 나타난 단어를 인접한 단어와 별다른 차이가 없는 동일한 key, value 벡터로 본다
  - 그래서 필요한 만큼의 정보를 바로 attention의 기반한 유사도가 높도록 함으로써 그 정보를 직접적으로 한번에 가져올수 있게 된다
  - 따라서 self-attention의 path length는 $O(1)$ 가 된다

Transformer: Block-Based Model

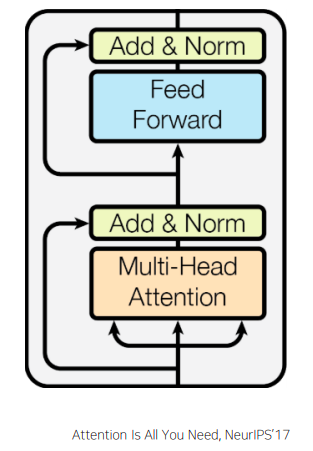
추가적인 연산 residual connection 이라고 부르는 Add operation을 수행한 후 layer normalization 을 수행하게 된다
또한 추가적으로 Feed Forward 네트워크를 통과하고 residual connection을 수행하게 된다
high-level에서는 여전히 주어진 입력 sequence가 residual connection에 이어서 Feed Forward 네트워크를 통해서 나오는 결과는 각각의 단어별 벡터에 적용되는 것이기 때문에 최종적으로 나오는것은 역시 동일한 차원을 가지는 각각의 단어에 대응하는 encoding vector가 된다

Add operation에 해당하는 residual connection 설명

residual connection은 computer vision쪽에서 깊은 layer에 neural net을 만들때 gradient vanishing 문제를 해결하여 학습은 안정화 시키면서 layer를 계속 쌓아감에 따라 더 높은 성능을 보일수 있도록 하는 효과적인 모델이다
입력 벡터의 encoding(output) vector와 입력벡터를 각각 더해준다
multi-head attention을 통해 만들고자 하는 벡터가 입력 벡터의 encoding(output) vector와 입력벡터를 각각 더해준 값이라고 하면 multi-head attention 모듈에서는 결국 입력값 대비 만들고자하는 벡터의 대한 차이값만을 만들면 된다
이러한 과정을 통해 gradient vanishing 문제도 해결하고 학습도 좀 더 안정화 시킬수 있게 된다
residual connection을 적용하기 위해서는 입력 벡터와 encoding의 output 으로 나타나는 출력벡터 간의 dimension이 정확하게 동일하도록 유지되어야 한다 그래야 각 dimension 별로 해당 원소값을 더해서 최종 동일한 차원을 가지는 벡터 만들어 줄수 있다
output layer에 해당하는 선형변환에서는 일시적으로 head 수가 많아짐에 따라서 encoding vector 의 output들이 concat이 되면서 차원이 늘어나게 되고 그 늘어난 차원을 원래 입력 벡터와 더해줘야 하기 때문에 입력 벡터와 동일한 차원을 가지는 벡터로 선형변환을 수행해야 한다

Norm(layer normalization)에 해당하는 residual connection 설명

여러 normalization layer는 주어진 다수의 샘플들에 대해서 값들의 평균을 0 분산을 1로 만들어준 후 사용자가 원하는 평균과 분산을 주입할수 있도록 하는 선형변환으로 이루어진다

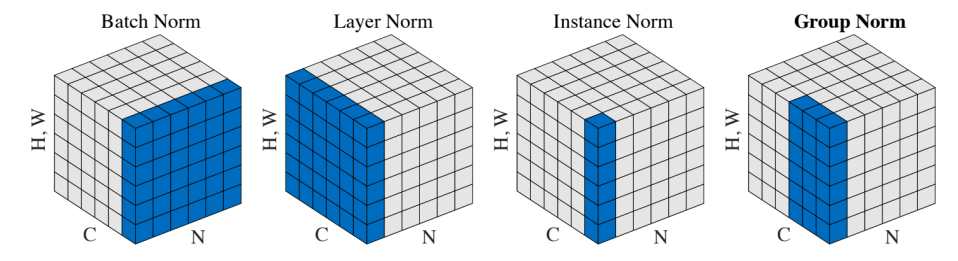
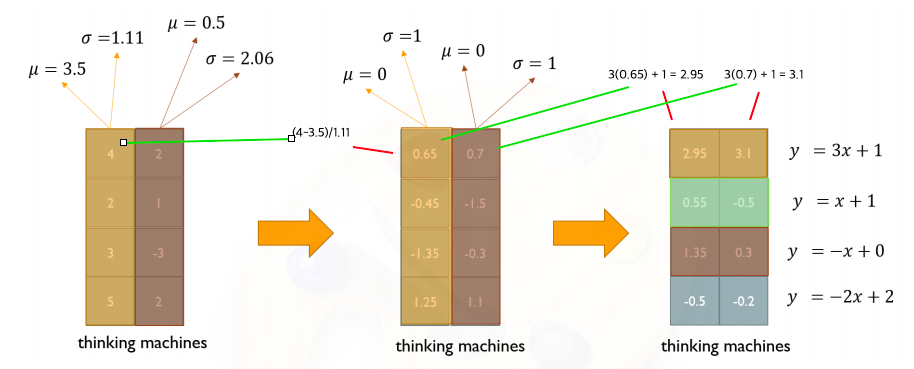
layer norm은 두 단계로 구성되어있다 :
- 첫번째 단계에서는 주어진 샘플들에 대한 평균 분산을 0 과 1로 만들고 - 두번째는 원하는 평균과 분산을 주입하기 위한 affine transformation( $y=ax + b$ ) 과정을 수행(Affine transformation of each sequence vector with learnable parameters)
- 첫번째 단계에서 column vector를 기준으로 standardization(평균을 0 분산을 1)과정을 수행했다면
- 두번째 단계 affine transformation에서는 layer에서 발견된 각 노드별로 동일한 변환을 수행하게 된다

layer norm은 학습을 안정화하고 최종적인 성능을 끌어올리는데 중요한 역할을 한다

Transformer: Positional Encoding

순서의 측면에서 'I go home' 이라는 문장을 'home go I'의 순서로 encoding을 했을때를 생각해보면
원래 순서에서 가지던 'I'의 최종 encoding vector output과 순서를 뒤집었을때 동일한 단어 'I' 에 해당하는 encoding vector output은 동일하게 벡터 결과가 나올 것이다
이는 attention 모듈을 수행할때 key, value 벡터 페어들은 순서에 전혀 상관없이 각 key 별로 주어진 query와의 attention유사도를 구하고 해당 value 벡터에 가중치를 부여해서 가중합을 함으로써 주어진 입력 벡터에 대한 encoding output vector 을 얻어내는데
주어진 가중 평균을 낼때 value vector들이 교환 법칙이 성립되기 때문에 최종 encoding output vector는 순서에 영향없이 동일하다
이렇게 순서를 무시한다는 특성은
- 입력 문장을 sequence정보를 고려해서 encoding을 하지 못하고 이것을 마치 순서를 고려하지 않은 집합으로 보고 각 집합에서의 원소의 encoding을 얻는 과정으로 생각할수 있다
이 경우 RNN 과는 다른 차이점이 생긴다
- RNN에서는 순서가 바뀌게 되면 각 단어들에 대한 hidden state vector의 정보가 적층되는 순서가 달라지기 때문에 encoding output vector도 달라지게 된다
- 그렇기 때문에 RNN은 자연스럽게 sequence 를 인식하고 구별해서 encoding output vector를 얻어내는 기법이지만
- Transformer(self-attention)모델은 순서를 반영할수 없는 한계점을 가지게 된다
그래서 나온것이 transformer 에서 사용되는 positional encoding이 있다
- 직관적인 예시:
  - 가령 'I go home' 에서 'I' 가 가지는 입력 벡터가 3차원 벡터로서 3, -2, 4 라는 벡터로 생각한다
  - 입력 벡터 'I'에 해당하는 벡터를 이 'I'라는 단어가 전체 sequence에서 첫번째 위치에 등장했다라는 것을 벡터에 포함시켜준다
  - 예시로 첫번째 위치에 발견된 단어인 경우 첫번째 dimension에 1000이라는 숫자를 더해주는것이다
  - 그럼 이 경우 이 벡터는 1003, -2, 4 가 될것이다
  - 가령 이 벡터가 3번째 위치에 나타난 경우라면 세번째 dimension에 1000을 더해주게 되면 해당 벡터는 3, -2, 1004 가 된다
  - 그렇다면 벡터 1003, -2, 4 과 벡터 3, -2, 1004 명확하게 차이가 날것이고 같은 입력벡터에서 시작했다 하더라도 그 위치에 따라 서로 다른 값을 가지게 된다
- 핵심 아이디어는 각 순서를 규정할수 있는 unique한 상수 벡터를 각순서에 등장하는 단어의 입력 벡터에 더해주는데 이것을 positional encoding이라 한다
- 더해주는 벡터를 결정하는 방법:
  - $PE_{(pos,2i)}=sin(\frac{pos}{10000^{\frac{2i}{d_{model}}}})$
  - $PE_{(pos,2i+1)}=cos(\frac{pos}{10000^{\frac{2i}{d_{model}}}})$
  - 위치에 따라 구별할수 있는 벡터를 sine과 cosine으로 이루어진 주기함수를 사용하고 그 주기를 서로 다른 주기를 사용해서 여러 sine함수를 만든 후 거기서 발생된 특정 x값에서의 함수값을 모아서 위치를 나타내는 벡터로 사용하게 된다

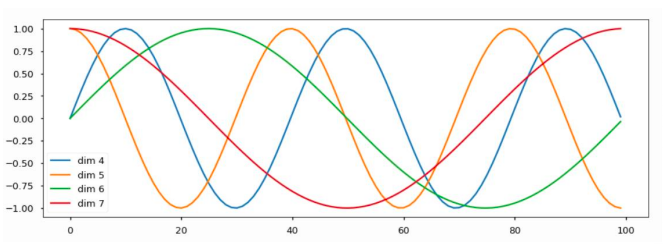
각 dimension 별로 sine혹은 cosine함수를 이렇게 만드는데
- 위 그림에서 4번째 dimension은 sine 함수로 어떤 특정한 주기를 가지고
- 5번째 dimension은 cosine 함수로 어떤 특정 주기를 가지는 함수다
- 6번째는 4번째 dimension과는 주기가 다른 sine함수
- 7번째는 5번째 dimension과는 다른 주기를 갖는 cosine 함수
이렇게 차원 갯수만큼의 서로다른 주기와 sine 혹은 cosine이 서로 번갈아가며 그래프가 생성되는 패턴을 만들어놓은 후
첫번째를 0번 인덱스라고 하면 0번에서의 position encoding vector 즉 입력벡터에 더해주는 즉, 첫번째 위치를 나타내는 unique한 vector를 4번째 dimension에서는 파랑색 그래프에서 얻는다
- 각각 차원에 맞는 그래프에서 positional encoding vector를 얻는다
이러한 방식으로 순서를 구분하지 못했던 self-attention 모듈에 기본적인 한계점을 위치별로 서로 다른 벡터가 더해지도록 함으로써 위치가 달라지면 출력 encoding vector도 달라지게 하는 방식으로 순서라는 정보를 transformer 모델이 다룰수 있도록 극복했다

Transformer: Warm-up Learning Rate Scheduler

$learning rate = d_{model}^{-0.5} \cdot min(\#step^{-0.5}, \#step \cdot warmup\_steps^{-1.5})$
일반적으로 gradient descent 및 adam 등의 최적화를 수행하는 과정에서 사용되는 learning rate(hyper-parameter)를 학습 과정동안 하나의 고정된 값으로써 사용하게 되는데 학습을 좀 더 빠르게 하고 최종수렴한 모델의 성능도 고정 learning rate을 썻을때 보다 더 올릴수 있게 하는 목적으로써 learning rate 값도 학습중에 적절히 변경되서 사용하는 기법을 learning rate scheduler 라고 부른다
초반에는 learning rate을 작은 값으로 사용한다
- 작은 값을 사용해서 해당 gradient의 절대값이 클 때 작은 learning rate값이 곱해지게 되므로써 큰 보폭이 발생되는것을 방지한다
어느정도 iteration이 진행되면 좀더 완만한, gradient의 절대값이 작은 값에 도달할수 있는데 이 경우는 도달해야하는 optimal point가 멀리 있을수 있기 때문에 동력을 주는 차원에서 점차로 learning rate을 iteration수에 비례해서 올려준다
근처까지 다온 상황에서는 learning rate을 크게 쓰면 보폭이 큼으로 인해서 정확한 저점에 도달하지 못하고 주변을 맴도는 현상이 일어난다
- 정확한 저점에 도달할수 있도록 learning rate을 점차 줄여주는 형태로 iteration이 진행됨에 따라 learning rate의 값을 동적으로 바꿔준다

Transformer: High-Level View

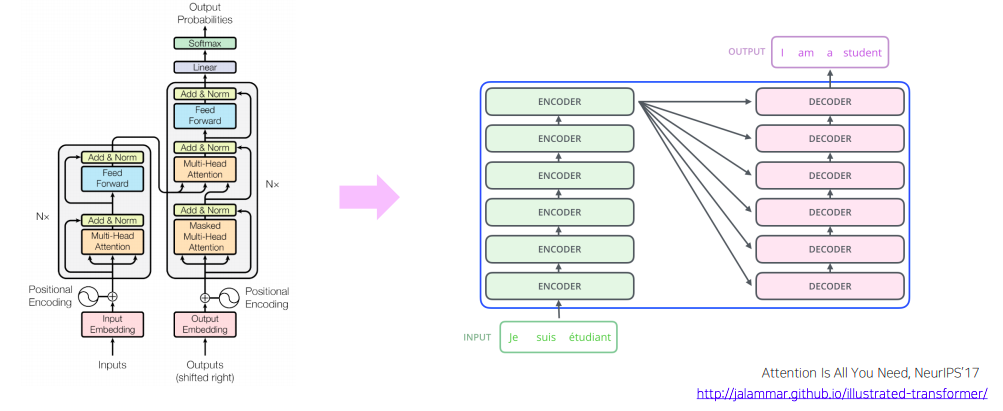
Nx = encoding block을 총 N번, 가령 N은 6, 12, 24 등의 값을 사용(각 블록은 독립적인 파라미터를 가지게 된다), 쌓아서 sequence에 각 단어에 해당하는 encoding vector가 점차로 high-level의 벡터로 encoding이 진행된다

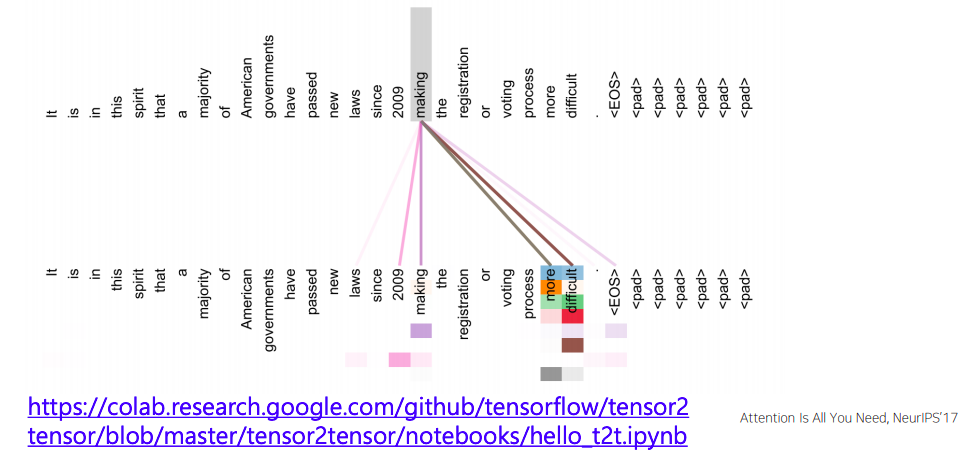
Transformer: Encoder Self-Attention Visualization

특정한 encoding 당시에 layer에서의 attention모듈에서의 패턴을 보면 다음과 같다
- 아래 그림에서 윗줄과 아랫줄이 동일한 문장인것으로 보이고 그래서 주어진 아랫줄의 각 단어의 입력 벡터가 attention모듈을 수행하면서 윗줄의 query, key, value 벡터들을 사용했을때 어떤식으로 정보를 가져가는지에 대한 패턴을 보여준다
- 'making'이라는 query자리의 벡터가 자기자신의 정보를 어느정도 가져가고 'more','difficult'에 해당하는 정보를 많이 가져가고 잇는것을 알수 있다
- 동시에 'making'이라는 형태의 액션이 언제부터 일어났는지에 대한 'since', '2009' 라는 시기정보를 가져가고 있는것을 볼수 있다
- 화살펴의 두께나 색깔 뿐만 아니라 같은 단어라 하더라도 여러 grid 형태가 보이는데 여기서의 grid는 각각 head의 attention 패턴을 의미한다
- 그래서 처음 4~5개 정도의 head에서는 'making'이 어떤 목적 보호에 해당하는 'more', 'difficult'한 상황으로 만들었다 라는 부분을 주로 많이 attention을 주면서 그 정보를 가져간것을 알수 있다
- 동시에 자기 자신을 attention하는 어떤 특정 head가 존재하고
- '2009'년이라는 시기 정보를 가져가는 head를 별도로 존재한다는 것을 알수 있다

여기까지 transformer 모델에서 encoder 부분을 다 cover를 했다
다음에는 입력 sequence를 받아서 출력 sequence를 예측을 해야하는 상황에서 decoding 을 어떻게 수행하는 살펴보자

Transformer: Decoder

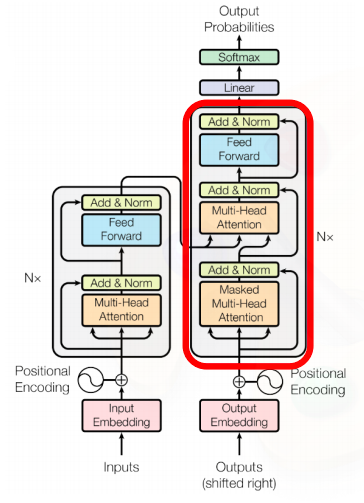
decoder에서 'I go home'이라는 문장이 주어졌을때 이를 encoding 하고 이를 '나는 집에 간다' 라는 문장으로 번역하는 경우로 생각해보자
Seq2Seq with attention 모델을 학습한 과정을 살펴보면 '< SOS > 나는 집에' 라는 단어가 학습 당시에 decoder의 입력 sequence로 주어진다
그다음에 여기서 나와야되는 단어는 바로 다음단어인 '간다' 가 출력 단어가 예측 단어로써 나와야 한다
decoder 상에서 원래 ground truth 문장인 '나는 집에 간다' 를 한칸 밀어서 '< S0S > 나는 집에' 이러한 형태의 입력 sequence를 각각의 embedding vector로써 주게 된다
이는 마찬가지로 positional encoding 을 거친 후 주어진 sequence를 multi-head attention으로 encoding으로 한 후 residual connection 그리고 layer normalization을 거쳐서 주어진 output sequence를 encoding 하는 과정을 먼저 거치게 된다
이 과정은 Seq2Seq with attention 모델에서 decoder에서의 hidden state vector를 뽑는 과정에 해당한다고 볼 수 있다
각각의 encoding vector '< SOS > 나는 집에 '가 decoder의 hidden state vector로 얻어졌다면 그 다음에는 다시 multi-head attention에 그단어를 입력으로 주는것을 알수 있다
그렇지만 여기서는 value, key, query 각각의 입력에 대해서 decoder에서 만들어진 hidden state vector가 query로 사용되고 encoding딴의 최종 출력 벡터가 key와 value 벡터로 사용되서 attention이 수행된다
이 부분이 seq2seq with attention 모델에서 추가적인 attention 모듈로써 여기 들어가는 decoder hidden state vector를 query 벡터로 해서 encoder의 hidden state vector 중 어느 vector를 가중치를 걸어서 해당 정보를 서로 다른 decoder의 time step에서 가져올지를 결정하는 encoder decoder 만의 attention 모듈이 이 부분에 해당한다
그 이후에는 다시 residual connection 과 layer normalization 그리고 추가적으로 feed forward layer 후 residual connection 마지막으로 layer normalization을 통해 최종적으로 '< SOS > 나는 집에' 에 해당하는 각각의 벡터가 어떤 decoder의 최종 encoding 벡터로써 나오게 된다
이 각각의 벡터는 residual connection에 의해서 어떤 decoder에 이문장에 대한 정보를 갖고 있음과 동시에 encoder에서 주어진 3개의 encoding output vector에 대한 정보를 각각에 decoder에 해당하는 매 time step 마다 서로 다른 정보를 가져와서 그 정보를 잘 결합한 형태의 벡터가 된다
최종적으로 각각의 벡터에 linear transformation 을 거친 후 softmax를 취하고 그래서 어떤 특정한 단어에 대한 확률값을 뽑아서 문장에대한 예측을 수행한다
그렇게해서 나온 단어들에 대한 분포는 ground truth 단어와의 softmax loss를 통해서 backpropagation에 의해 전체가 네트워크의 학습이 진행된다

Masked Multi-Head Attention

masked self-attention에서 masking을 하는 이유:
- cheating(예측해야하는 값(미래 시점의 값)을 미리 알고 학습을 하는 것)을 방지하기 위해
- 예를들어 “I go home” 문장이 있을 때, decoder의 input으로 “I”를 입력하면 “go”를 예측해야하는데, 그냥 self-attention을 수행하면 “I”의 encoding vector에는 “go”와 “home”의 정보가 들어가서 정확한 학습이 이루어지지 않음
- 여기서 masking을 통해 미래 시점에 대한 softmax값을 0이 되면, 가중평균 하는 과정에서 미래 시점에 대한 값이 0이 되기 때문에 해당 값들이 현재 시점의 encoding vector에 들어가지 않음
- 참고

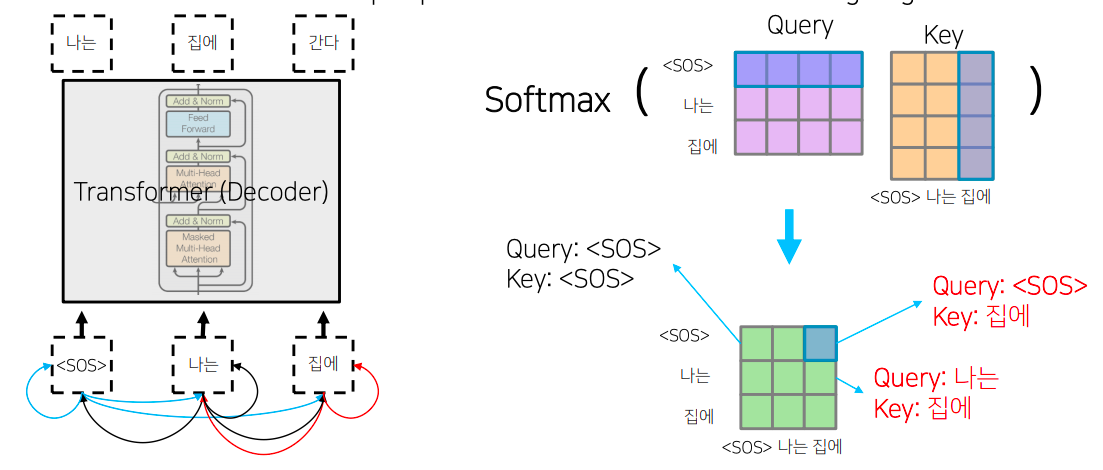
masked self-attention의 기본 아이디어는 decoding 과정 중에 입력으로써 '< SOS > 나는 집에' 라는 단어들을 주고 그 다음 단어를 예측하는 과정에서 주어진 sequence에 대해서 self-attention을 통해 sequence의 각 단어를 encoding 하는 과정에서 정보의 접근의 가능여부와 관련된다
가령 '< SOS > 나는 집에' 에 해당하는 단어에 대해서 이를 query 및 key, value로 사용하는 self-attention을 수행하는 경우 query, key 에 해당하는 $QK^T$ 를 계산하게 되면 결국 '< SOS >'를 query로 했을때 자기자신 '< SOS >' 라는 key를 과연 얼마정도의 유사도로 볼지
그리고 '< SOS >' 를 query로 했을때 '나는' 에 해당하는 단어를 얼마정도의 유사도로 볼지
혹은 '집에' 에 해당하는 단어를 얼마정도의 유사도로 볼지를 결정해주는 그런정보를 담고 있다
그런대 이렇게 해서 각 단어가 나머지 모든 단어들에 대해서 정보를 다 접근을 허용하게 되면 '< SOS >' 라는 단어 까지만 첫번째 time step에서 주어졌을때 이 경우 물론 학습 데이터에서 입력으로 주어야하는 단어들이 뒤에서 '나는' 과 '집에' 라는 단어가 주어져야 된다는것을 알지만
예측 과정을 생각해보면 '< SOS >'만 주어져 있고 여기서 '나는' 이라는 단어를 예측해야하고 '< SOS > 나는' 까지의 단어가 주어졌을때 '집에' 라는 단어를 예측하는 즉, 뒤에 나오는 단어를 학습당시에는 batch processing을 위해서 입력으로 동시에 주긴하나 '< SOS >'를 query로 사용해서 attention 모듈을 수행할때는 가능한 접근 가능한 key에서 '나는'과 '집에' 라는 단어는 제외해줘야 한다
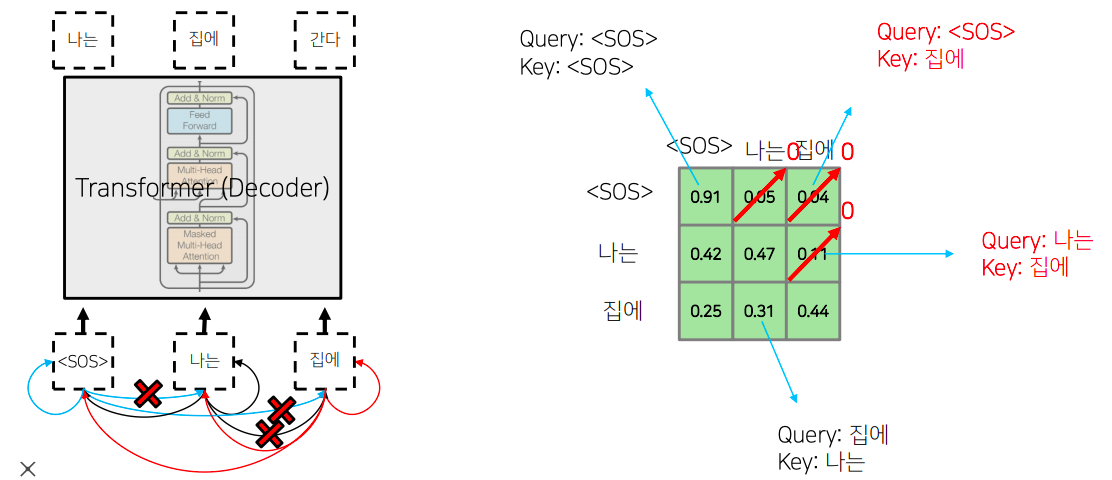
그렇게 되면 어떤 softmax 이후의 확률값이 계산이된 경우에는 결국 '< SOS >' 자기자신을 91% 두번째, 세번째로 나타나는 단어를 근소하지만 작은 확률로 본다라고 할때
여기서 정보를 가져올수 있는것은 차단해줘야 한다
그래서 softmax까지 구한 다음에는 이 값을 다 0으로 후처리 적으로 만들어준다
- 대각선 라인을 기준으로 윗부분에 해당하는 정보를 모두다 0으로 만들어주는 과정
그 다음엔 다시 row 별로 합이 1이 되도록 normalize를 하게 된다
Masked self-attention에 masking에 의미는 attention을 모두가 다 모두를 볼수있도록 허용한 후 후처리 적으로 보지 말아야되는, 뒤에서 나오는, 단어에 대한 attention의 가중치를 0으로 만들어주고
그 이후 value vector와 가중평균을 내는 방식으로 attention을 변형한 방식이 decoder에서 사용하는 masked self-attention이 된다

Transformer: Experimental Results

Results on English-German/French translation (newstest2014)
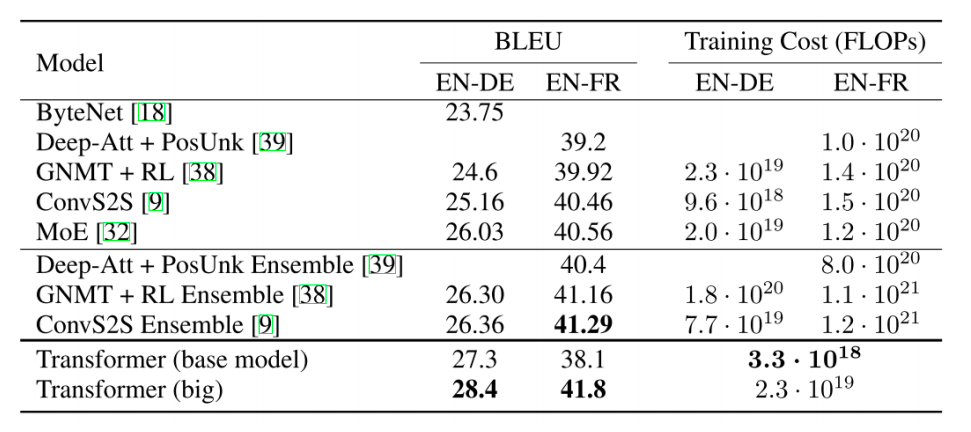
transformer 기반 모델이 가장 좋은 성능을 내느것을 알 수 있다
BLEU 값들에 경우 대략 20~40% 의 값을 가지는데
BLEU의 최대값이 100%라는 것을 감안하면 번역성능이 대략 26~40% 에 머문다는것을 볼수 있다
그렇지만 이게 보기보다는 훨씬 더 좋은 성능을 내는 결과에 해당된다
이것은 가령 '나는 수학을 열심히 공부한다' 라는 문장이 ground truth 문장이고
'나는 열심히 수학을 공부한다' 번역문장이 예측값으로 주어지는 경우는
두 문장이 동일한 문장이긴 해도 bi-gram, tri-gram, 4-gram으로 따졌을때는 해당 precision 값은 굉장히 낮아지게 된다
그렇기 때문에 40% 정도는 실질적으로 체감하는 번역성능은 실제로 google translate, naver papago 등의 사용화된 기계번역 서비스에 필적하는 성능이 된다