그래프의 구조를 어떻게 분석할까?
- 이번에는 그래프에서의 군집(Community)이 무엇인지 배우고, 군집에 대한 해석, 그래프에서 군집을 탐색하는 법에 대해 배운다
- 실제 세상에서 우리는 주변에서 여러가지 종류의 군집을 볼 수 있다
- 인간 관계 사이에서 (ex. 동아리, 동창회), 화학 물질 내부에서 등 어디서나 군집을 발견할 수 있다
- 그렇다면, 우리는 그래프 데이터에서 군집을 어떻게 정의하고, 어떻게 찾아낼까?
- 그래프 데이터에서 군집을 찾아내는 알고리즘을 배워보고, 실제로 적용까지 해보자
Further Reading
군집 구조와 군집 탐색 문제
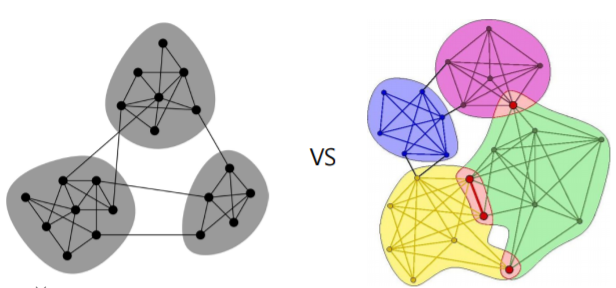
군집의 정의
- 군집(Community)이란 다음 조건들을 만족하는 정점들의 집합이다
- 집합에 속하는 정점 사이에는 많은 간선이 존재한다
- 집합에 속하는 정점과 그렇지 않은 정점 사이에는 적은 수의 간선이 존재한다
- '많은', '적은' 같은 수학적으로는 모호한 표현들이 사용됬기 때문에 수학적으로 엄밀한 정의는 아니다
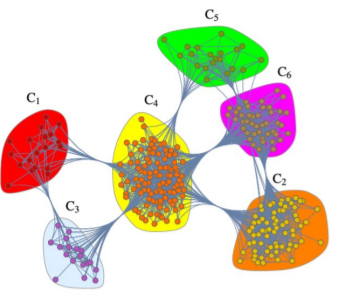
- 아래의 그래프에는 11 개의 군집이 있는 것으로 보인다

실제 그래프에서의 군집들
- 온라인 소셜 네트워크의 군집들은 사회적 무리(Social Circle)을 의미하는 경우가 많다
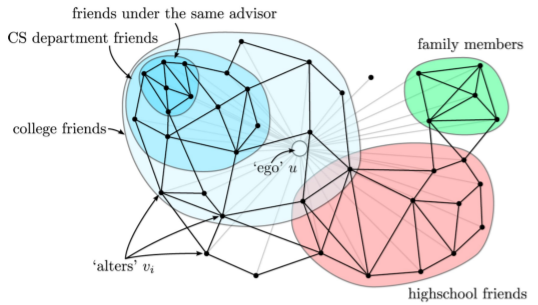
- 온라인 소셜 네트워크의 군집들이 부정 행위와 관련된 경우도 많다
- 아래 부정 행위에 연루된 계정들이 군집을 형성한다는 것을 발견할 수 있다
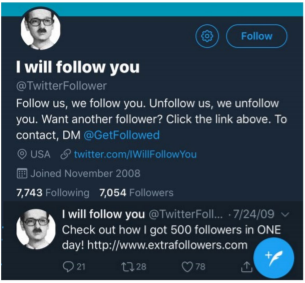
- 아래 부정 행위에 연루된 계정들이 군집을 형성한다는 것을 발견할 수 있다
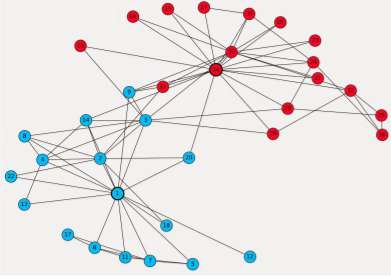
- 조직 내의 분란이 소셜 네트워크 상의 군집으로 표현된 경우도 있다
- 아래의 그래프는 대학교 가라테 동아리 내 친구 관계를 보여준다
- 내분으로 동아리가 둘로 나뉘어지는 사건이 발생했다
- 그 결과 두 개의 군집이 형성되었다
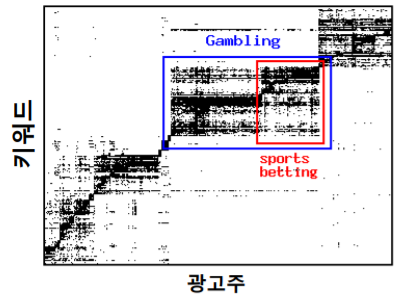
- 키워드 – 광고주 그래프에서는 동일한 주제의 키워드들이 군집을 형성한다
- 그래프를 인접행렬로 표현하게 되면 그래프내의 군집들은 인접행렬에서 0이 아닌 원소들이 밀집해 있는 것으로 나타난다
- 아래의 키워드-광고주 그래프 의 인접행렬을 시각화한 것이다
- 키워드-광고주 그래프 에서는 동일한 주제의 키워드들이 군집을 형성한다
- 가운데 큰 군집에 경우에는 도박과 관련된 키워드와 광고주들로 구성되어있고
- 그중에서도 빨간색 군집은 스포츠 도박과 관련된 키워드와 광고주로 구성되어있다
- 원소 중 0은 흰색, 나머지는 검은색으로 표시한 것이다
- 뉴런간 연결 그래프에서는 군집들이 뇌의 기능적 구성 단위를 의미한다
- 즉, 같은 군집에 속하는 뉴런들이 뇌의 특정기능을 담당한다
- 즉, 같은 군집에 속하는 뉴런들이 뇌의 특정기능을 담당한다
군집 탐색 문제
- 그래프를 여러 군집으로 ‘잘’ 나누는 문제를 군집 탐색(Community Detection) 문제라고 한다
- 보통은 각 정점이 한 개의 군집에 속하도록 군집을 나눈다
- 비지도 기계학습 문제인 클러스터링(Clustering)과 상당히 유사하다
- 먼저 성공적인 군집 탐색 부터 정의하자
- 군집구조가 성공적인지에 대한 여부를 비교를 통해 결정한다
- 그때, 비교의 대상이 되는것이 배치모형이다
- 이 비교를 통해서 군집 모형의 통계적 유의성(군집성)을 측정한다
군집 구조의 통계적 유의성과 군집성
비교 대상: 배치 모형
- 성공적인 군집 탐색을 정의하기 위해 먼저 배치 모형(Configuration Model)을 소개한다
- 주어진 그래프에 대한 배치 모형 은,
- 각 정점의 연결성(Degree)을 보존 한 상태에서
- 간선들을 무작위로 재배치 하여서 얻은 그래프를 의미한다
- 배치 모형에서 임의의 두 정점 와 사이에 간선이 존재할 확률은 두 정점의 연결성에 비례합니다
- 주어진 그래프에 대한 배치 모형 은,
군집성의 정의
- 군집 탐색의 성공 여부를 판단하기 위해서, 군집성(Modularity)이 사용된다
- 그래프 와 군집들의 집합 S 가 주어졌다고 하자
- 각 군집 가 군집의 성질을 잘 만족하는 지를 살펴보기 위해, 군집 내부의 간선의 수를 그래프 와 배치 모형 에서 비교한다
- 구체적으로, 군집성 은 다음 수식으로 계산된다

- |E| : 간선의 갯수
- 2|E| : 곱하기 2를 하는 이유는 총 degree의 합이, 간선 하나가 왼쪽 정점과 오른쪽 정점 둘다한테 degree를 1씩 주기때문에 간선 하나당 degree 2에 해당되서 2|E|가 된다
- 2|E| 로 나누어서 정규화를 해줘야 하는 이유는
- 아래 군집 탐색 알고리즘(girvan-newman, louvain)의 매 iteration 마다 간선의 갯수가 달라지기 때문에(girvan-newman 같은 경우 매 iteration 마다 매개 중심성이 높은 간선을 제거) 매 iteration 마다 나오는 군집성에 대한 정당한 비교를 위해 정규화를 실행한다
- 기댓값을 사용하는 이유는 배치 모형이 무작위성을 포함하고 있기 때문이다
- 배치모형 에서 군집 s 내부 간선의 수가 그래프에서 군집 s 내부 간선의 수 보다 적게 나올 수 있는 경우의 예시:
- 그래프 노드가 {1,2,3,4,5,6,7,8,9}로 구성되있는 그래프가 있다고 생각해보자
- 군집 기준을 {1,2,3}, {4,5,6}, {7,8,9}로 잡았을때
- 배치 모형이 어떻게 만들어지느냐에 따라서 각 군집의 내부 간선수가 달라질 수 잇다
- 군집 {7,8,9} 에서 8의 degree가 만약 2면 그 간선이 7과 9로 갈수도 있지만 1,2,3,4,5,6 쪽으로도 갈수도 있기 때문에 내부 간선수는 달라질수 있다
- 즉, 배치모형 과 비교했을 대, 그래프 에서 군집 내부 간선의 수가 월등이 많을 수록 성공한 군집 탐색이다
- 즉, 군집성은 무작위로 연결된 배치 모형과의 비교를 통해 통계적 유의성을 판단한다
- 군집성 은 정규화를 통해 항상 –1과 +1 사이의 값을 갖는다
- 보통 군집성이 0.3 ~ 0.7 정도의 값을 가질 때, 그래프에 존재하는 통계적으로 유의미한 군집들을 찾아냈다고 할 수 있다
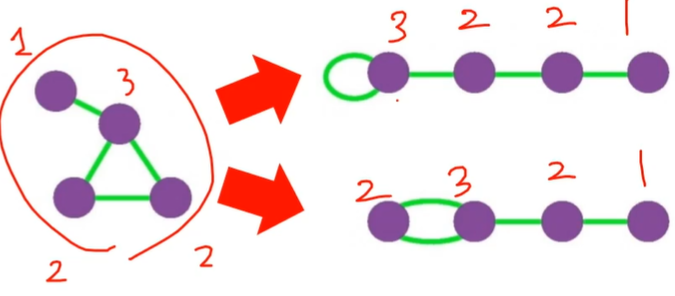
두 정점 사이의 간선 개수의 기댓값 (in more detail)

- 위 식에서 두 정점 사이의 간선 개수의 기댓값:
- stub :
- 아래 그림은 모든 간선을 반으로 가른 것이다
- 여기서 반으로 갈린 간선이 stub 이다
- 정점의 stub 개수를 로 표기하고 정점의 stub 개수를 로 표기
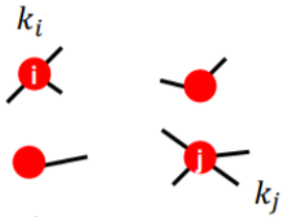
- 원본 그래프의 간선의 수가 개 일 때, 모든 stub의 개수는 다음과 같다
- 각 간선이 반으로 갈라졌으므로 두 배가 된 것이다
- 원본 그래프와 간선수가 같은 null model(배치모형)을 생각해보자
- 이 모델은 stub들을 이어서 만들기 때문에 간선수는 같다
- 정점의 stub이 정점의 stub과 edge를 이룰 확률은 다음과 같다
- 여기서 는 stub이 edge를 이뤘으면 1, 아니면 0이 되는 값이다
- 기댓값은 값 x 확률이므로, 값이 1이 되는 확률이 곧 간선수의 기댓값이다
- 전체 경우의 수는 자신을 제외한 모든 stub의 개수 이고, 관심 경우의 수는 정점의 stub 개수다
- 따라서 정점과 정점의 edge 개수의 기댓값은 다음과 같다
- m이 충분히 크면, 분모의 -1은 무시 가능하다
- 모든 정점에서 모든 정점에 대해서 계산하면 간선수의 기댓값은 다음과 같다
- 이 중 summation에서 각각 간선은 두 번식 카운팅 되므로, 를 곱해준 것이다
- 이 사용된다
- stub :
모듈성(군집성) (in more detail)

- 위 식을 아래와 같이 표현이 가능하다
- 은 그래프의 총 간선 수)
- 우선 군집별 간선수와 간선수 기댓값 차이의 총합을 구해보면,
- 군집 간선수는 인접행렬 에 대응
- 군집 간선수 기댓값은 degree를 이용하여 구함
- 모듈별 군집 간선수 기댓값의 총합은
- 한 군집의 인접행렬(앞 항) summation 식을 살펴보면
- 최솟값은 0 (원래 인접 정점들이었던 정점들이 서로 다른 군집에 속하는 경우)
- 최댓값은 4m (원래 인접 정점들이었던 정점들이 모두 같은 군집에 속하는 경우)
- 에 대해 2배(가 중복됨)
- 에 대해 2배(마찬가지)
- 모든 군집에 대해 summation하면 0~4m의 값을 가진다
- 기댓값(뒷 항) 을 빼주면 -2m ~ 2m의 값을 가진다
- 따라서 2m으로 나누어 주어, -1 ~ 1의 값을 갖도록 한다
- 그러나 가 너무 커서 계산량이 많기 때문에 근사값을 쓴다
군집 계수 vs 군집성
- 군집 계수(Clustering Coefficient)(Local or Global) 는 네트워크가 얼마나 잘 뭉쳐있는지를 나타내는 값이다
- 군집성(Modularity) 는 그래프에서 각 정점마다 군집 몇 번에 속하는 지를 부여한 다음 그렇게 나누는 것이 잘 나누어졌는지 판단하는 값이다
- 군집계수 가 높다면(네트워크에 노드들이 잘 뭉쳐있다면), 그만큼 군집을 나눌 때도 쉽게 잘 나뉠 것이고 군집성(Modularity) 도 그만큼 올라가게 될 것이다
- 반대로, 규모가 엄청난 랜덤그래프 의 경우 군집 계수 가 매우 낮을텐데 이러한 그래프는 군집도 잘 나뉘지 않을 것이고 군집성(Modularity) 도 매우 낮게 측정될 것이다
군집 탐색 알고리즘
Girvan-Newman 알고리즘
- Girvan-Newman 알고리즘은 대표적인 하향식(Top-Down) 군집 탐색 알고리즘이다
- Girvan-Newman 알고리즘은 전체 그래프에서 탐색을 시작한다
- 군집들이 서로 분리되도록, 간선을 순차적으로 제거 한다
- 어떤 간선을 제거 해야 군집들이 분리될까?
- 바로 서로 다른 군집을 연결하는 다리(Bridge) 역할 의 간선이다
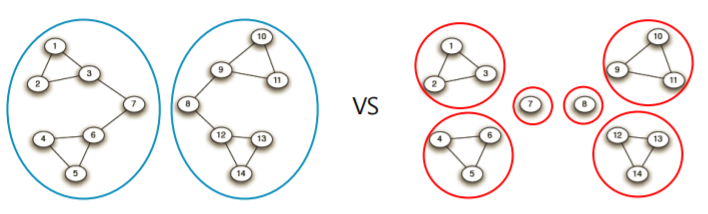
- 아래 예시에서 파란색 선 을 따라 간선을 제거한다고 생각해보자
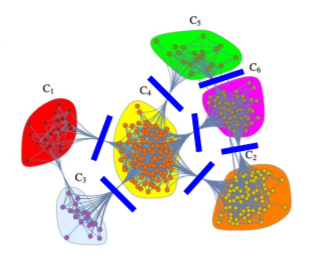
- __서로 다른 군집을 연결하는 다리 역할의 간선을 어떻게 찾아낼 수 있을까?
- 간선의 매개 중심성(Betweenness Centrality) 을 사용한다
- 이는 해당 간선이 정점 간의 최단 경로에 놓이는 횟수 를 의미한다
- 정점 로 부터 로의 최단 경로 수를 라고 하고 그 중 간선 ()를 포함한 것을 라고 하자
- 간선 ()의 매개 중심성 은 다음 수식으로 계산된다
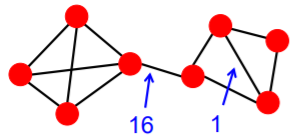
- 위 그래프의 개운데 간선에 경우 왼쪽에 존재하는 4개의 정점과 오른쪽에 존재하는 4개의 정점을 최단경로로 연결하기 위해서는 반드시 지나야 하는 간선이다
- 즉, 왼쪽 4개 x 오른쪽 4개 총 16개의 정점 쌍의 최단경로에 놓이는 간선이다
- 따라서 이 간선의 매개 중심성 은 16이다
- 반면 오른쪽에 있는 간선의 경우 오로지 두 개의 정점 사이의 최단경로에만 놓이는 간선이다
- 따라서 이 간선의 매개 중심성 은 1이다
- 매개 중심성을 통해 서로 다른 군집을 연결하는 다리 역할의 간선을 찾아낼 수 있다
- 아래 그림은 전화 그래프이다
- 매개 중심성 이 높을 수록 붉은 색에 가깝다
- 실제로 매개 중심성 이 높은 간선들이 서로 다른 군집을 연결하는 다리 역할 을 하는 것을 확인할 수 있다
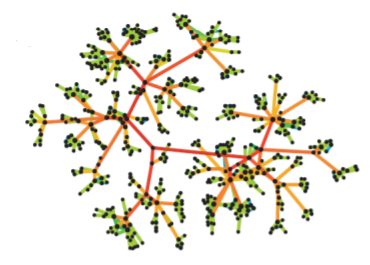
- 아래 그림은 전화 그래프이다
- Girvan-Newman 알고리즘은 매개 중심성이 높은 간선을 순차적으로 제거 한다
-
간선이 제거될 때마다, 매개 중심성을 다시 계산하여 갱신한다
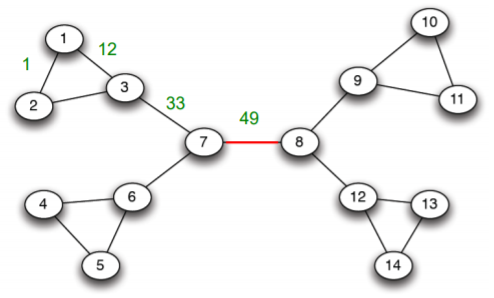
-
간선이 모두 제거될 대까지 반복한다

-
간선의 제거 정도(iteration)에 따라서 다른 입도(Granularity)의 군집 구조 를 나타낸다
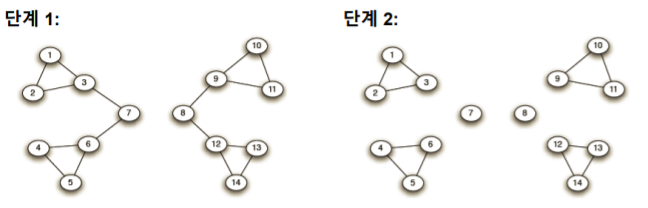
- 간선을 두 개만 제거했을때는 전체 그래프를 2개의 군집으로 나누는것을 알수 있고
- 간선을 추가로 4개를 제거했을대는 전체 그래프를 6개의 군집으로 나누는것을 알 수 있다
- 둘 중에 어느정도의 입도가 더 적적한 입도 일까?
-
- 간선을 어느 정도 제거하는 것이 가장 적합할까?
- 앞서 정의한 군집성 을 그 기준으로 삼는다
- 즉, 군집성이 최대가 되는 지점까지 간선을 제거한다
- 단, 현재의 연결 요소 각각을 군집으로 가정하여 군집성을 계산한다
- 즉, 입력 그래프가 두개의 연결 요소로 나뉘었을때는 두 개의 군집이 있다고 가정하고 군집성을 계산하고
- 입력 그래프가 6개의 연결 요소로 나뉘었을때는 6개의 군집이 있다고 가정하고 군집성을 계산한다
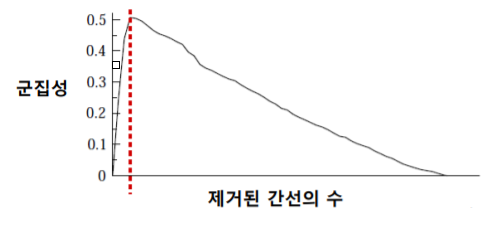
- 아래 그림의 예시는 제거된 간선의 수의 따라 군집성이 어떻게 변하는지를 보여주고 있다
- 빨간색 선의 위치한 간선의 수를 제거하였을때 군집성이 최대가 된다
- 따라서 빨간색 선의 위치한 간선의 수를 제거 됬을때의 입력 그래프의 상태를 복원해 낸뒤
- 그때의 입력 그래프의 연결 요소들을 군집으로 간주한다
- 앞서 정의한 군집성 을 그 기준으로 삼는다
- 정리하면, Girvan-Newman 알고리즘은 다음과 같다
- 전체 그래프에서 시작한다
- 매개 중심성 이 높은 순서로 간선을 제거하면서, 군집성 의 변화를 기록한다
- 군집성 이 가장 커지는 상황을 복원한다
- 이 때, 서로 연결된 정점들, 즉 연결 요소를 하나의 군집으로 간주한다
- 즉, 전체 그래프에서 시작해서 점점 작은 단위를 검색하는 하향식(Top-Down) 방법이다
- 어떤 정점이 어떤 군집에 속하는지에 대한 정보가 레이블로 주어져 있지 않더라도 그래프의 구조를 분석함으로써 그것을 추론해낼 수 있다
Louvain 알고리즘
- Louvain 알고리즘은 대표적인 상향식(Bottom-Up) 군집 탐색 알고리즘이다
-
각 정점이 하나의 군집을 형성한다고 가정한 상태에서 시작한다
- 즉, 아래 예시에선느 총 15개의, 하나의 정점으로 구성된, 군집이 있다고 가정한다
-
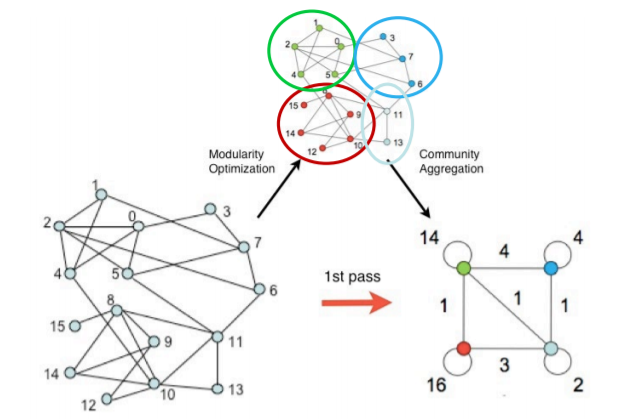
Louvain 알고리즘은 개별 정점에서 시작해서 점점 큰 군집을 형성한다
- 이 과정을 하나의 pass 라고 한다
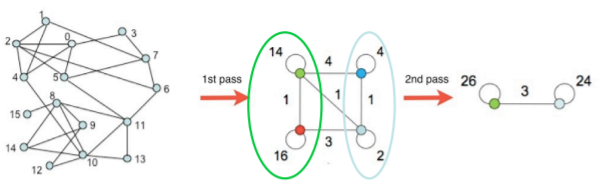
- 군집단위로 표현된 그래프에서 한번더 pass를 거치게 된다
- 즉 군집들을 병합하는 과정을 한번더 거친다
-
- 그러면 어떤 기준으로 군집을 합쳐야 할까?
- 정답은 이번에도 군집성 이다
- 구체적으로 Louvain 알고리즘의 동작 과정은 다음과 같다
- 첫째) Louvain 알고리즘은 개별 정점으로 구성된 크기 1의 군집 들로부터 시작한다
- 둘째) 각 정점 를 기존 혹은 새로운 군집으로 이동한다
- 이 때, 군집성이 최대화 되도록 군집을 결정한다
- 셋째) 더 이상 군집성이 증가하지 않을 때까지 두번째를 반복한다
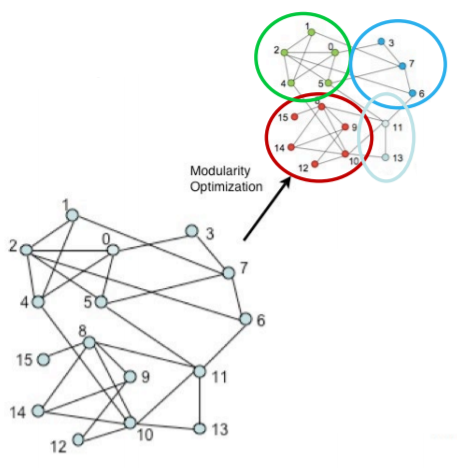
- 넷째) 각 군집을 하나의 정점으로하는 군집 레벨의 그래프를 얻은 뒤 세번째를 수행한다
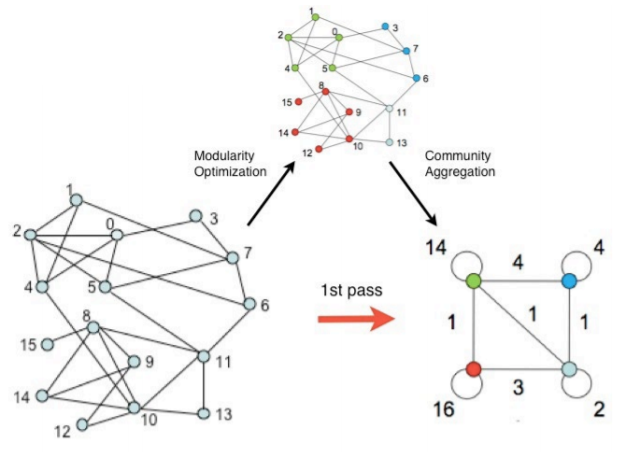
- 한 개의 정점이 남을 때까지 4번째를 반복한다
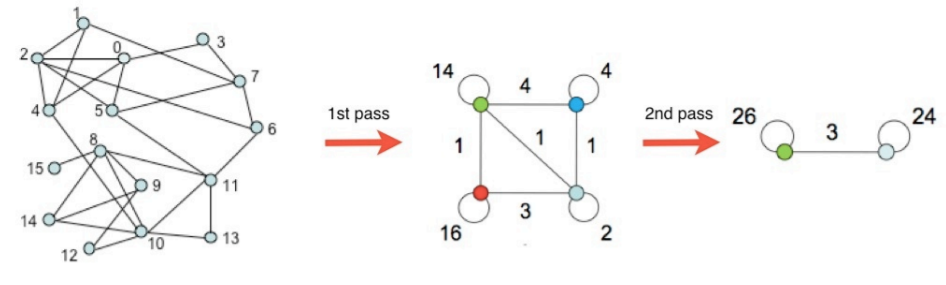
Louvain 알고리즘을 이용해 소셜 네트워크의 군집을 탐색한 결과를 살펴보자
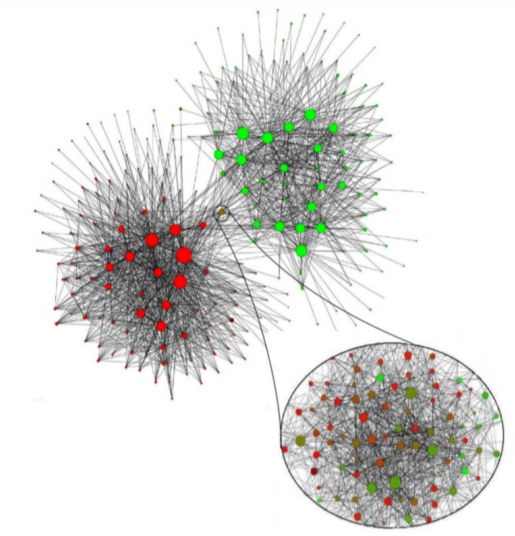
- 그래프의 정점들은 실제로는 여러 정점들로 구성된 군집 이다
- 불어 를 사용하는 사람의 비율이 높을 수록 녹색 에, 독어 를 사용하는 사람의 비율이 높을 수록 붉은색 에 가깝다
- 대부분 군집들이 높은 비율의 불어를 사용하는 사람들 혹은 높은 비율의 독어를 사용하는 사람들 로 구성되어 있다
- 예외적으로 가운데 군집 하나는 두 언어를 사용하는 사람들이 혼합되어 있으며, 다리 역할을 합니다
중첩이 있는 군집 탐색
중첩이 있는 군집 구조
- 실제 그래프의 군집들은 중첩되어 있는 경우가 많다
- 예를 들어 소셜 네트워크에서의 개인은 여러 사회적 역할 을 수행한다
- 그 결과 여러 군집 에 속하게 된다
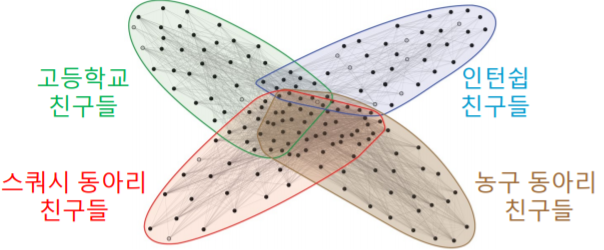
- 그 결과 여러 군집 에 속하게 된다
- 예를 들어 소셜 네트워크에서의 개인은 여러 사회적 역할 을 수행한다
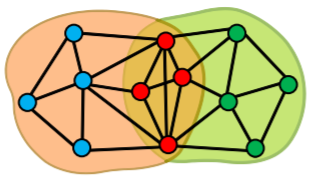
- __앞서 배운 Girvan-Newman 알고리즘, Louvain 알고리즘은 군집 간의 중첩이 없다고 가정한다
- 즉, 한개의 정점은 오직 한개의 군집에만 속할수 있다
- 그렇다면 오른쪽에 있는 그림처럼 중첩이 있는 군집들 즉, 한개의 정점이 여러개의 군집에 속할수 있는 경우에는 어떻게 군집을 찾아낼 수 있을까?
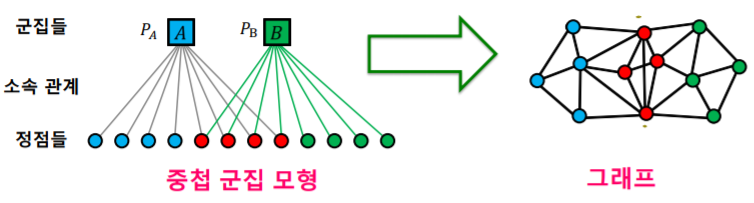
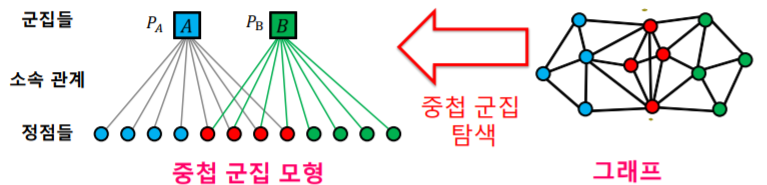
중첩 군집 모형
- 이를 위해 아래와 같은 중첩 군집 모형을 가정한다
- 각 정점은 여러 개의 군집에 속할 수 있다
- 각 군집 에 대하여, 같은 군집에 속하는 두 정점은 확률로 간선으로 직접 연결된다
- 두 정점이 여러 군집에 동시에 속할 경우 간선 연결 확률은 독립적이다
- 즉, 가 성립하게 된다
- 예를 들어, 두 정점이 군집 와 에 동시에 속할 경우 두 정점이 간선으로 직접 연결될 확률은 1 − (1 − )(1 − ) 이다
- 여기서 군집 와 모두에 속하지 않을 확률은 먼저 주어진 조건처럼 독립적이므로 (군집 A에 속하지 않을 확률)×(군집 B에 속하지 않을 확률)와 같다
- 즉, (1 - )×(1 - )가 된다
- 이 결과를 위에 대입하면 결과적으로 간선으로 연결된 두 정점이 군집 와 에 동시에 속할 경우는 1 - (1 - )×(1 - )가 성립한다
- 어느 군집에도 함께 속하지 않는 두 정점은 낮은 확률 으로 직접 연결됩니다
- 중첩 군집 모형이 주어지면, 주어진 그래프의 확률을 계산할 수 있다
- 그래프 의 확률은 다음 확률들의 곱이다
- 그래프의 각 간선의 두 정점이 (모형에 의해) 직접 연결될 확률
- 그래프에서 직접 연결되지 않은 각 정점 쌍이 (모형에 의해) 직접 연결되지 않을 확률
- 그래프 의 확률은 다음 확률들의 곱이다
커뮤니티 모형과 완화된 커뮤니티 모형
- 현실에 많은 경우에는 그래프는 주어져 있지만 중첩된 군집 모형이 주어지지 않은 경우가 많다
- 따라서 중첩 군집 탐색은 주어진 그래프의 확률을 최대화하는 중첩 군집 모형을 찾는 과정이다
- 통계 용어를 빌리면, 최우도 추정치(Maximum Likelihood Estimate)를 찾는 과정이다
- 이 추정 과정은 쉽지 않다
- 그 이유는 각 정점이 각 군집에 속하는지 여부가 '속한다', '속하지 않는다' 같이 이산적(discrete)으로 결정되기 때문이다
- 따라서 연속된 값을 갖는 매개변수 즉, continuous 한 파라미터들을 최적화하는데 사용할 수 있는 각종 최적화 기술들(경사하강법)을 사용할 수가 없다
- 통계 용어를 빌리면, 최우도 추정치(Maximum Likelihood Estimate)를 찾는 과정이다
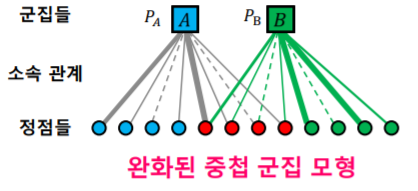
완화된 중첩 군집 모형
- 중첩 군집 탐색을 용이하게 하기 위하여 완화된 중첩 군집 모형을 사용한다
- 완화된 중첩 군집 모형 에서는 각 정점이 각 군집에 속해 있는 정도 를 실숫값 으로 표현한다
- 즉, 기존 모형에서는 각 정점이 각 군집에 속하거나 속하지 않거나 둘 중 하나였는데, 중간 상태를 표현할 수 있게 된 것이다
- 이 모형이 굉장히 현실적이다
- 왜냐하면 사람은 여러개의 군집에 속해 있지만 어떤 군집에는 더 소속감을 느끼며 더 많이 참여하고 다른 군집에는 소속감을 덜 느끼고 참여를 덜 할 수 있기 때문이다
- 위 그림에서는 각 소속 관계에 부여되는 실수값을 해당하는 간선의 두께로 표현했다
- 즉, 기존 모형에서는 각 정점이 각 군집에 속하거나 속하지 않거나 둘 중 하나였는데, 중간 상태를 표현할 수 있게 된 것이다
- 완화된 중첩 군집 모형에서의 최적화 관점에서는, 모형의 매개변수들이 실수 값(연속된 값)을 가지기 때문에 익숙한 최적화 도구(경사하강법 등)을 사용하여 모형을 탐색 할 수 있다는 장점이 있다
