추천 시스템

그래프를 추천시스템에 어떻게 활용할까? (기본)

• 넷플릭스와 유투브의 컨텐츠 추천, 아마존의 상품 추천 등 우리는 일상생활 속 다양한 곳에서 추천 시스템을 사용하고 있다
• 이번 강의에서는 다양한 형태의 추천시스템 중 아이템의 내용을 사용해 추천해주는 '내용 기반 추천(contents based recommendation')과, 유저와 아이템간의 유사도를 통해 추천을 해주는 '협업 필터링(collaborative filtering)'에 대해 살펴보자
• 각 알고리즘의 장단점에 집중하면서 보자

Further Reading

• recommendation systems

우리 주변의 추천 시스템

아마촌에서의 상품 추천

• Amazon.com 메인 페이지에는 고객 맞춤형 상품 목록을 보여준다
• 또한 Amazon.com 에서 특정 상품을 살펴볼 때, 함께 혹은 대신 구매할 상품 목록을 보여준다
  

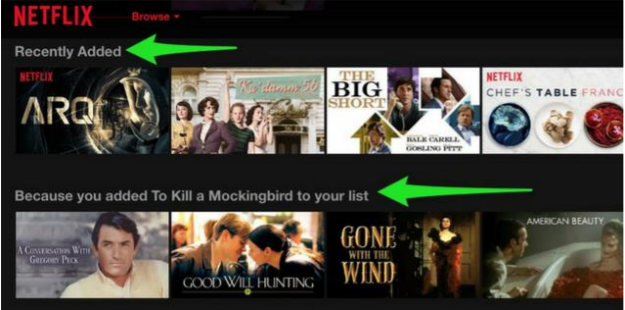
넷플릭스에서의 영화 추천

• 넷플릭스 메인 페이지에는 최신 영화 뿐만 아니라 고객 맞춤형 영화 목록을 보여준다
  

유튜브에서의 영상 추천

• 유튜브 메인 페이지에는 고객 맞춤형 영상 목록을 보여준다
  • 즉, 각 고객이 좋아할 만한 영상들의 목록을 추려서 보여준다
• 또한 유튜브는 현재 재생 중인 영상과 관련된 영상 목록을 보여준다

페이스북에서의 친구 추천

• 페이스북에서는 추천하는 친구의 목록을 보여준다

• 이처럼 추천의 대상은 다양하지만 이 노트에서는 편의상 상품을 추천하다고 가정하겠습니다

추천 시스템과 그래프

• 추천 시스템은 사용자 각각이 구매할 만한 혹은 선호할 만한 상품/영화/영상을 추천한다
  • 사용자별 구매 기록은 아래 예시처럼 그래프 로 표현 가능하다
  • 구매 기록이라는 암시적(Implicit)인 선호 만 있는 경우도 있고, 평점이라는 명시적(Explicit)인 선호 가 있는 경우도 있다
    
  • 추천 시스템의 핵심은 사용자별 구매 를 예측하거나 선호 를 추정하는 것이다
  • 그래프 관점에서 추천 시스템은 “미래의 간선을 예측하는 문제” 혹은 “누락된 간선의 가중치를 추정하는 문제” 로 해석할 수 있다
    

내용 기반 추천시스템

내용기반 추천시스템의 원리

• 내용 기반(Content-based) 추천 은 각 사용자가 구매/만족했던 상품과 유사한 것 을 추천하는 방법이다
• 예시는 다음과 같다
  • 동일한 장르의 영화를 추천하는 것
  • 동일한 감독의 영화 혹은 동일 배우가 출현한 영화를 추천하는 것
  • 동일한 카테고리의 상품을 추천하는 것
  • 동갑의 같은 학교를 졸업한 사람을 친구로 추천하는 것
  • 이 추천들의 공통점은 장르, 감독, 배우, 카테코리, 나이, 학교 등 수 많은 부가 정보들을 활용했다
    • 이러한 부가 정보들 을 활용하여 유사한 상품 을 찾아내는것이 내용 기반 추천 시스템 의 핵심 아이디어다
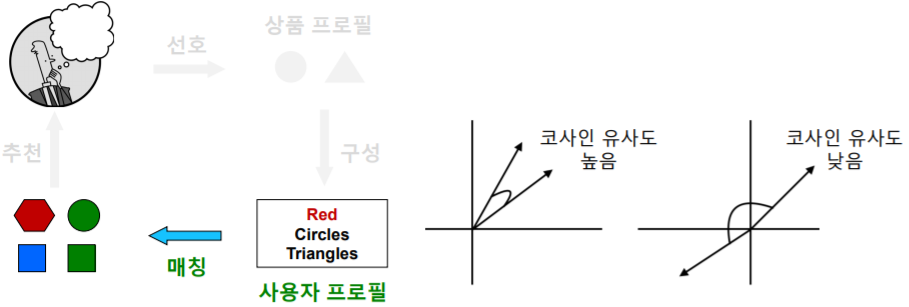
• 내용 기반 추천은 다음 네 가지 단계 로 이루어진다
  
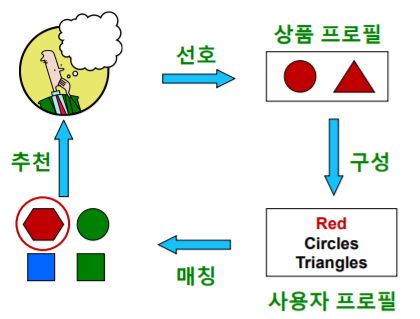
• 첫 단계 는 사용자가 선호했던 상품들의 상품 프로필(Item Profile) 을 수집하는 단계이다
  • 어떤 상품의 상품 프로필 이란 해당 상품의 특성을 나열한 벡터 이다
  • 영화의 경우 감독, 장르, 배우 등의 원-핫 인코딩 이 상품 프로필이 될 수 있다
    
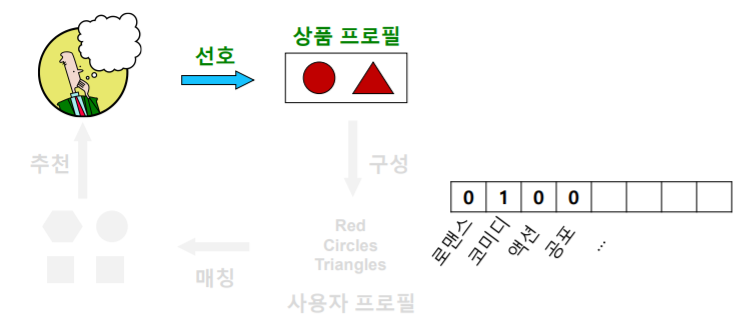
• 다음 단계 는 사용자 프로필(User Profile) 을 구성하는 단계다
  • 사용자 프로필 은 선호한 상품의 상품 프로필을 선호도를 사용하여 가중 평균하여 계산한다
  • 즉 사용자 프로필 역시 벡터이다
  • 앞선 영화 프로필 예시에서는 다음과 같은 형태의 사용자 프로필을 얻을 수 있다
    
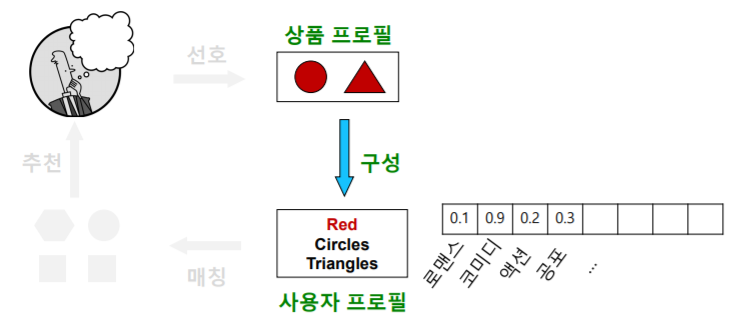
• 다음 단계 는 사용자 프로필과 다른 상품들의 상품 프로필을 매칭 하는 단계이다
  • 사용자 프로필 벡터 $\vec{𝑢}$ 와 상품 프로필 벡터 $\vec{𝑣}$ 코사인 유사도 $\frac{\vec{u} \cdot \vec{v}}{||\vec{u}|| \; ||\vec{v}||}$ 를 계산한다
    • 즉, 두 벡터의 사이각의 코사인 값을 계산한다
    • 코사인 유사도는 두 벡터의 내적값 나누기 두 벡터의 크기의 곱으로 정의된다
  • 코사인 유사도 가 높을 수록, 해당 사용자가 과거 선호했던 상품들과 해당 상품이 유사함을 의미한다
    - 벡터의 크기 : 벡터의 Norm 2 값
    
• 마지막 단계 는 사용자에게 상품 을 추천하는 단계다
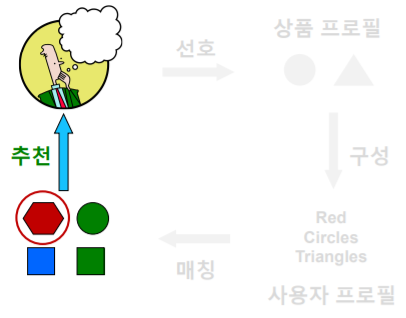
  • 계산한 코사인 유사도가 높은 상품 들을 추천합니다
    

내용 기반 추천시스템의 장단점

• 장점 :
  • 다른 사용자의 구매 기록이 필요하지 않다
    • 사용자 본인의 과거 기록만을 이용하여 추천한다
  • 독특한 취향 의 사용자에게도 추천이 가능하다
  • 새 상품 에 대해서도 추천이 가능하다
    • 새 상품에 대한 사람들의 평가가 없더라도 이 상품이 가진 속성 정보를 이용하여 추천한다
  • 추천의 이유 를 제공할 수 있다
    • 코사인 유사도에서 큰 일치가 발생한 부분을 가지고 추천의 이유를 제공할 수 있다
    • 예시: 당신은 로맨스 영화를 선호했기 때문에, 새로운 로맨스 영화를 추천합니다
• 단점 :
  • 상품에 대한 부가 정보가 없는 경우 에는 사용할 수 없다
    • 상품 프로필 자체가 부가 정보를 이용하여 구성하기 때문이다
  • 구매 기록이 없는 사용자 에게는 사용할 수 없다
    • 구매 기록을 바탕으로 사용자 프로필을 구성하기 때문이다
  • 과적합(Overfitting)으로 지나치게 협소한 추천 을 할 위험이 있다
    • 사용자가 우연히 어떤 편향된 선택을 했을때 그 편향으로 추천이 계속 치우치는 협소한 추천 문제가 발생할 수 있다

협업 필터링 추천시스템

• 내용 기반 추천시스템의 단점을 일부 보안하는 추천시스템

협업 필터링의 원리

• 사용자-사용자 협업 필터링 은 다음 세 단계로 이루어진다
  • 추천의 대상 사용자를 $𝑥$라고 하자
  • 우선 $𝑥$ 와 유사한 취향의 사용자들 을 찾는다
  • 다음 단계로 유사한 취향의 사용자들 이 선호한 상품 을 찾는다
  • 마지막으로 이 상품 들을 $𝑥$ 에게 추천한다
  • 즉 사용자-사용자 협업 필터링이란, 대상 사용자와 유사한 취향을 가진 다른 사용자들이 선호했던 상품을 추천하는 방법
    
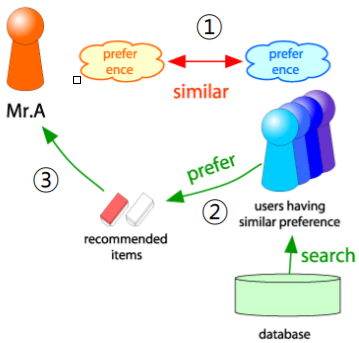
• 사용자-사용자 협업 필터링의 핵심은 유사한 취향의 사용자 를 찾는 것이다
• 그런데 취향의 유사도 는 어떻게 계산할까?
  • 아래 예시는 사용자 별 영화 평점이다
  • '?'는 평점이 입력되지 않은 경우를 의미한다
  • 지수와 제니의 취향이 유사하고, 로제는 둘과 다른 취향을 가진 것을 알 수 있다

• 취향의 유사성은 상관 계수(Correlation Coefficient) 를 통해 측정

  • 사용자 $𝑥$의 상품 $𝑠$에 대한 평점을 $𝑟_{𝑥𝑠}$라고 하자
  • 사용자 $𝑥$가 매긴 평균 평점을 $\bar{r_x}$라고 하자
  • 사용자 $𝑥$와 $𝑦$가 공동 구매한 상품들을 $S_{𝑥𝑦}라고 하자
  • 사용자 $𝑥$와 $𝑦$의 취향의 유사도 는 아래 수식으로 계산한다
    • $sim(x,y) = \cfrac{\sum_{s \in S_{xy}} (r_{xs} - \bar{r_x})(r_{ys}-\bar{r_y})}{\sqrt{\sum_{s \in S_{xy}}(r_{xs}-\bar{r_x})^2} \sqrt{\sum_{s \in S_{xy}} (r_{ys} - \bar{r_y})^2}}$
    • 즉, 통계에서의 상관 계수(Correlation Coefficient)를 사용해 취향의 유사도를 계산한다

• 예시에서 취향의 유사도 를 계산해보자

  • 둘이 함께 본 영화만을 고려한다
  • 지수와 제니의 취향의 유사도는 0.88 이다
    • $\frac{(4-3)(5-3)+(1-3)(1-3)+(5-3)(4-3)}{\sqrt{(4-3)^2+(1-3)^2+(5-3)^2}\sqrt{(5-3)^2+(1-3)^2+(4-3)^2}}$
    • 즉 둘의 취향은 매우 유사 하다
  • 지수와 로제의 취향의 유사도는 -0.94 이다
    • $\frac{(4-3)(2-4)+(1-3)(5-4)+(2-3)(5-4)}{\sqrt{(4-3)^2+(1-3)^2+(2-3)^2}\sqrt{(2-4)^2+(5-4)^2+(5-4)^2}}$
  • 즉 둘의 취향은 매우 상이 하다
  • 따라서, 지수의 취향을 추정할 때는 제니의 취향을 참고하게 된다
    • 예를 들면, 지수는 미녀와 야수를 좋아할 확률이 낮다
    • 지수와 제니의 취향은 유사하고, 제니는 미녀와 야수를 좋아하지 않기 때문이다

• 구체적으로 취향의 유사도를 가중치로 사용한 평점의 가중 평균 을 통해 평점을 추정 한다

  • 사용자 $𝑥$의 상품 $𝑠$에 대한 평점을 $𝑟_{𝑥𝑠}$를 추정하는 경우를 생각해보자
  • 앞서 설명한 상관 계수를 이용하여 상품 $𝑠$를 구매한 사용자 중에 $𝑥$와 취향이 가장 유사한 𝑘명 의 사용자 $𝑁(𝑥; 𝑠)$를 뽑는다
  • 평점 $𝑟_{𝑥𝑠}$는 아래의 수식을 이용해 추정한다
    • $\hat{r_{xs}} = \cfrac{\sum_{y \in N(x;s)}sim(x,y) \cdot r_{ys}}{\sum_{y \in N(x;s)}sim(x,y)}$
    • 즉, 취향의 유사도를 가중치로 사용한 평점의 가중 평균을 계산한다

• 마지막 단계는 추정한 평점이 가장 높은 상품을 추천 하는 단계이다

  • 추천의 대상 사용자를 $𝑥$라고 하자
  • 앞서 설명한 방법을 통해, $𝑥$가 아직 구매하지 않은 상품 각각에 대해 평점을 추정한다
  • 추정한 평점이 가장 높은 상품 들을 $𝑥$에게 추천한다

협업 필터링의 장단점

• 장점
  • 상품에 대한 부가 정보가 없는 경우 에도 사용할 수 있다
• 단점
  • 충분한 수의 평점 데이터가 누적 되어야 효과적이다
  • 새 상품, 새로운 사용자 에 대한 추천이 불가능하다
  • 독특한 취향의 사용자 에게 추천이 어렵다

추천 시스템의 평가

데이터 분리

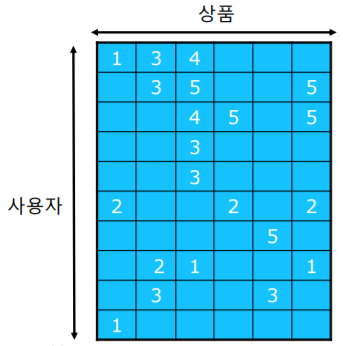
• 평점 데이터는 행렬이라고 생각할 수 있다

• 추천 시스템의 정확도는 어떻게 평가할까?
  

• 먼저 데이터를 훈련(Training) 데이터 와 평가(Test) 데이터 로 분리한다
  

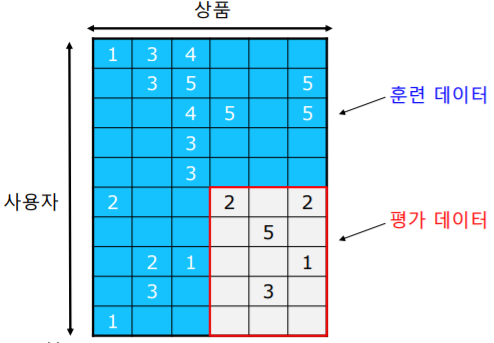
• 평가 데이터 는 주어지지 않았다고 가정한다
  

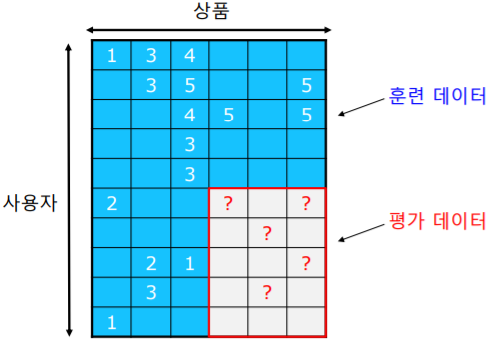
• 훈련 데이터를 이용해서 가리워진 평가 데이터의 평점을 추정 한다
  

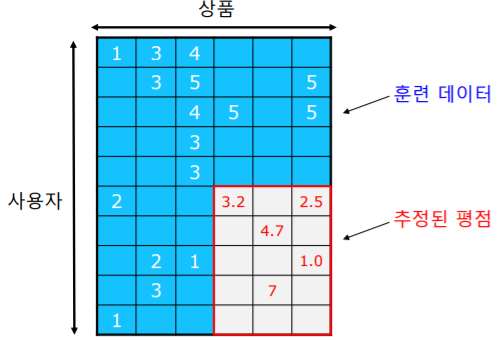
• 추정한 평점과 실제 평가 데이터를 비교 하여 오차를 측정한다
  

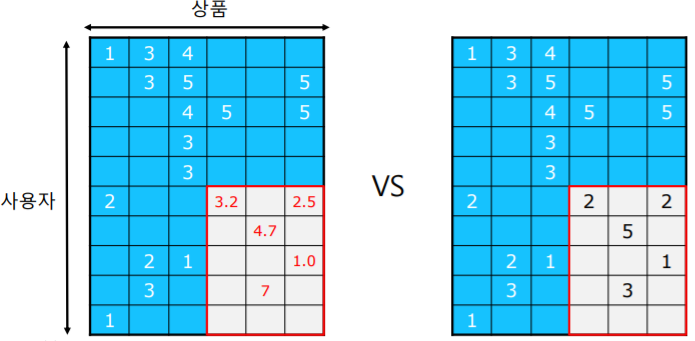
평가 지표

• 오차를 측정하는 지표로는 평균 제곱 오차(Mean Squared Error, MSE) 가 많이 사용된다
• 평가 데이터 내의 평점들을 집합을 $𝑇$ 라고 하자
• 평균 제곱 오차 는 아래 수식으로 계산된다
  • $\frac{1}{|T|} \sum_{r_{xi} \in T} (r_{xi} - \hat{r_{xi}})^2$
• 평균 제곱근 오차(Root Mean Squared Error, RMSE) 도 많이 사용된다
  • $\sqrt{\frac{1}{|T|} \sum_{r_{xi} \in T} (r_{xi} - \hat{r_{xi}})^2}$
• 이 밖에도 다양한 지표가 사용된다
  • 추정한 평점으로 순위를 매긴 후, 실제 평점으로 매긴 순위와의 상관 계수 를 계산하기도 한다
  • 추천한 상품 중 실제 구매로 이루어진 것의 비율 을 측정하기도 한다
  • 추천의 순서 혹은 다양성까지 고려하는 지표 들도 사용된다