모델의 시공간

• 이번 강의는 모델의 탐색 시간복잡도에 대한 내용이다
• 모델의 시간복잡도를 줄이는 것은 경량화의 목적 중 하나이다
• 여기에서는 시간복잡도를 Big-Oh Notation으로 정의한다
• 모델의 시간복잡도를 구성하는 요소는 크게 세 가지이다
  1) parameter search
  2) hyperparameter search
  3) architecture search
• 여기에서는 위의 세 가지 요소를 다루면서 Search에 대한 내용을 다룬다

Further Questions

• regular convolution 대신 depthwise seperable convolution을 사용해서 계산상의 가장 큰 이득을 보는 경우는 언제일까?
• (동전 말고) 주사위의 경우에는 maximum entropy가 얼마나 될까?

미니 코드

Time complexity

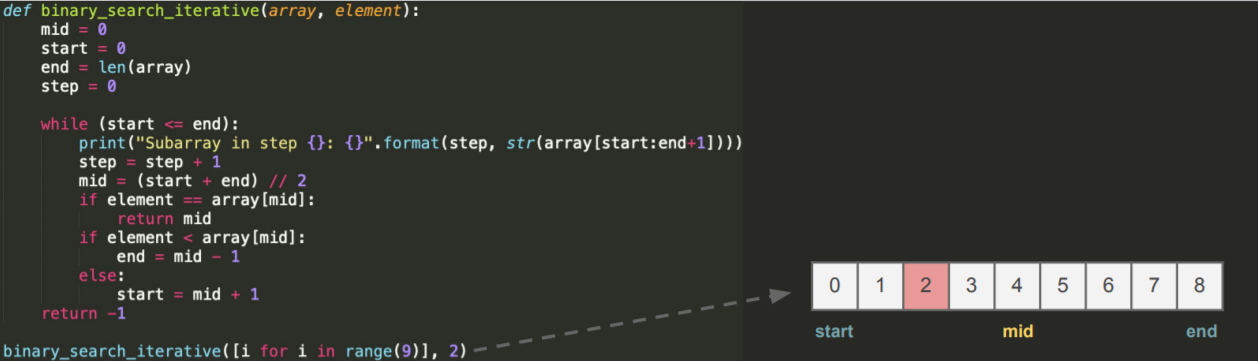
• problem space : input이 들어간것과 원하는 output
• search space : # of step 들이 몇번이나 일어나는지

Time-space Trade-off in Algorithms

• In computer science, a space-time or time-memory tradeoff is a way of solving a problem or calculation in less time by using
  more storage space (or memory), or by solving a problem in very little space by spending a long time. Most computers have a
  large amount of space, but not infinite space. Also, most people are willing to wait a little while for a big calculation, but not
  forever. So if your problem is taking a long time but not much memory, a space-time tradeoff would let you use more memory
  and solve the problem more quickly. Or, if it could be solved very quickly but requires more memory than you have, you can try
  to spend more time solving the problem in the limited memory.
• A space-time trade-off can be applied to the problem of data storage. If data stored is uncompressed, it takes more space but
  less time. But if the data is stored compressed, it takes less space but more time to run the decompression algorithm. There
  are many instances where it is possible to directly work with compressed data. In that case of compressed bitmap indices,
  where it is faster to work with compression than without compression.

Entropy

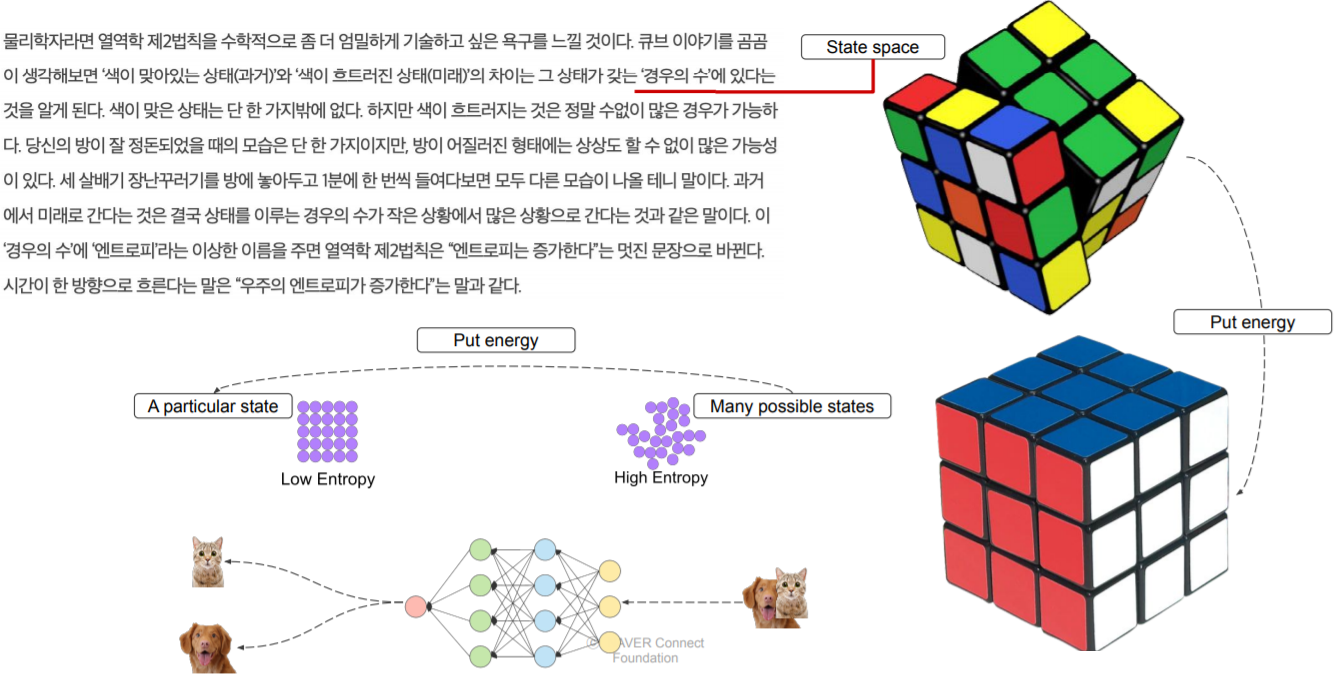
• 모델도 entropy 와 하는일이 비슷하다
  • 위 예시를 보게되면 개고양이 흐트러진 상태를 모델에 넣으므로써 low entropy 상태로 변환 시킨다
  • 미래(흐트러진) 상태에서 과거(정렬된) 상태로 되돌린다