검색 엔진에서는 그래프를 어떻게 활용할까?
- 이번에는 페이지랭크(PageRank) 알고리즘을 배운다
- 인터넷엔 인터넷 페이지가 셀 수 없이 많다
- 그리고 네이버나 구글 등의 검색엔진들은 우리가 입력한 키워드에 적합한 페이지들을 보여준다
- 검색엔진들은 어떻게 우리가 원하는 페이지들을 알려줄까요? 페이지들의 우선순위는 어떻게 결정하는 걸까요?
- 이번 시간에는 구글의 검색 알고리즘인 페이지랭크 알고리즘을 배우고 페이지랭크 알고리즘에서 발생할 수 있는 문제점과 이를 해결할 수 있는 알고리즘을 추가적으로 배운다
Further Reading
페이지랭크의 배경
웹과 그래프
- 웹은 웹페이지 와 하이퍼링크 로 구성된 거대한 방향성 있는 그래프 이다
- 웹페이지는 정점에 해당한다
- 웹페이지가 포함하는 하이퍼링크는 해당 웹페이지에서 나가는 간선에 해당한다
- 단, 웹페이지는 추가적으로 키워드 정보를 포함하고 있다
구글 이전의 검색 엔진
- 첫번째 시도는 웹을 거대한 디렉토리로 정리하는 것이었다
- 웹페이지의 수가 증가함에 따라서 카테고리의 수와 깊이 도 무한정 커지는 문제가 있다
- 참고로 현재는 수십억 ~ 수백억 개의 웹페이지 가 있는 것으로 알려져 있다
- 또한, 카테고리 구분이 모호한 경우가 많아, 저장과 검색에 어려움이 있다
- 두번째 시도는 웹페이지에 포함된 키워드에 의존한 검색 엔진이다
- 사용자가 입력한 키워드에 대해, 해당 키워드를 (여러 번) 포함한 웹페이지를 반환한다
- 하지만, 이 방법은 악의적인 웹페이지에 취약하다는 단점이 있다
- 예를 들어, 성인 사이트에 '축구'라는 키워드를 (보이지 않도록) 여러 번 포함하게 되면, '축구'를 검색했을 때 해당 성인 사이트가 결과로 나올 수 있다
- 사용자 키워드와 관련성 이 높고 신뢰 할 수 있는 웹페이지를 어떻게 찾을 수 있을까?
- 구글의 창업자인 래리 페이지(Larry Page)와 세르게이 브린(Sergey Brin)은 The PageRank Citation Ranking: Bringing Order to the Web 라는 제목의 논문을 통해 페이지 랭크 알고리즘을 소개한다
페이지랭크의 정의
투표 관점
- 페이지랭크의 핵심 아이디어는 투표이다
- 즉, 투표를 통해 사용자 키워드와 관련성이 높고 신뢰할 수 있는 웹페이지를 찾는다
- 투표의 주체는 바로 웹페이지이다
- 웹페이지는 하이퍼링크를 통해 투표를 한다
- 사용자가 키워드를 포함한 웹페이지들을 고려하자
- 웹페이지 u가 v로의 하이퍼링크를 포함한다면?
- u의 작성자가 판단하기에 v가 관련성이 높고 신뢰할 수 있다는 것을 의미한다
- 즉, u가 v에게 투표했다고 생각할 수 있다
- 즉, 들어오는 간선이 많을수록 신뢰할 수 있다는 뜻이다
- 논문을 고를 때도 마찬가지이다
- 사람들은 많이 인용된 논문을 더 많이 신뢰한다
- 그런데 들어오는 간선의 수를 세는 것만으로는 악용될 소지가 있다
- 웹페이지를 여러 개 만들어서 간선의 수를 부풀릴 수 있다
- 즉, 관련성과 신뢰도가 높아 보이도록 조작할 수 있다
- 또한 온라인 소셜 네트워크에서는 돈을 주고 트위터의 팔로원 수를 구매할수 있다 즉, 돈을 주고 들어오는 간선의 수를 늘릴수 있다
- 악용을 막으려면 어떻게 해야 할까?
- 이런 악용에 의한 효과를 줄이기 위해, 페이지랭크에서는 가중 투표 를 한다
- 즉, 관련성이 높고 신뢰할 수 있는 웹사이트의 투표를 더 중요하게 간주한다
- 반면, 그렇지 않은 웹사이트들의 투표는 덜 중요하게 간주한다
- 악용이 없는 경우에도 사용할 수 있는 합리적인 투표 방법이다
- 관련성과 신뢰성은 상요자가 투표를 통해 측정하려는 것 아니었나? 투표에 관련성과 신뢰성을 상요하자는 이야기는 출력을 입력으로 사용하자는 이야기처럼 들린다
- 그렇다. 재귀(recursion) , 즉 연립방정식 풀이를 통해 가능하다
- 측정하려는 웹페이지의 관령성 및 신뢰도를 페이지랭크 점수라고 부르자
- 각 웹페이지는 각각의 나가는 이웃에게
- 나가는이웃의수자신의페이지랭크점수 마큼의 가중치로 투표를 한다
- 아래의 그림에서 웹페이지 j는 웹페이지 x,y,z에게 각각 가중치 3rj 으로 투표를 한다
- rj는 웹페이지 j의 페이지 랭크 점수를 의미한다
- 비슷하게 i 정점을 살펴보자
- i 정점은 3개의 나가는 간선을 가지고 있고 그 중에 한개의 나가는 간선으 j와 연결되어있다
- 이 간선을 통해 i 는 j에게 3ri 만큼의 투표를 진행하게 된다
- 이때 ri 는 정점 i의 페이지랭크 점수의 해당한다
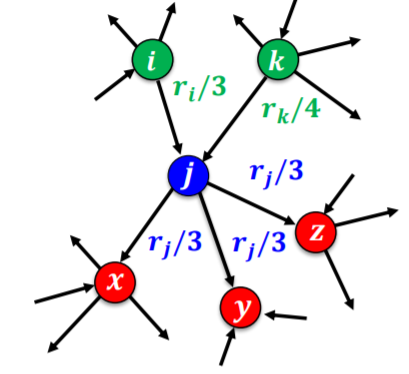
- 각 웹페이지의 페이지랭크 점수 는 받은 투표의 가중치 합으로 정의된다
- 위 그림에서 웹페이지 j의 페이지랭크 점수 rj는 다음과 같다
- rj=3rj+4rk
- 페이지랭크 점수 의 정의는 다음과 ㄱ같다
- rj=∑i∈Nin(j)dout(i)ri
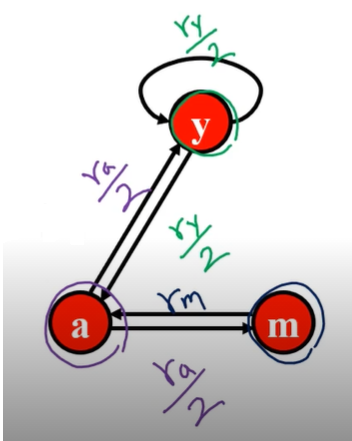
- 아래의 예시에서의 정점 별 페이지랭크 식은 다음과 같다
- ry=2ry+2ra
- ra=2ry+rm
- rm=2ra
- 변수 3개 식이 3개이므로 연립방정식을 통해 풀 수 있다
- 아래 그래프에서 특이한 점은, 웹페이지 y가 본인 스스로에게 하이퍼링크를 포함하고 있다
- 이 하이퍼링크는 정점 y에서 출발하여 정점 y에 도착하는 특이한 형태의 간선으로 표현됬다
임의 보행 관점
- 페이지랭크는 임의 보행(random walk)의 관점에서도 정의할 수 있다
- 임의 보행을 통해 웹을 서핑하는 웹서퍼 를 가정하자
- 즉, 웹서퍼는 현재 웹페이지에 있는 하이퍼링크 중 하나를 균일한 확률로 클릭하는 방식으로 웹을 서핑한다
- 웹서퍼가 t번째 방문한 웹페이지가 웹페이지 i일 확률을 pi(t)라고 하자
- 그러면 p(t)는 길이가 웹페이지 수(정점의 수)와 같은 확률분포 벡터가 된다
- 그러면 아래의 식이 성립한다
- pj(t+1)=∑i∈Nin(j)dout(i)pi(t)
- 웹서퍼가 이 과정을 무한히 반복하고 나면, 즉 t가 무한히 커지면,
확률 분포는 p(t)는 수렴하게 된다
- 다시 말해 p(t)=p(t+1)=p 이 성립하게 된다
- 수렴한 확률 분포 p는 정상 분포(Stationary Distribution) 라고 부른다
- 그러면 앞서 소개한 수식을 아래와 같이 바꿀 수 있습니다
- pj(t+1)=∑i∈Nin(j)dout(i)pi(t)⇒pj=∑i∈Nin(j)dout(i)pi
- 이 수식은 투표 관점에서 정의한 페이지 랭크 점수와 동일하다
- 투표 관점에서 정의한 페이지랭크 점수 r :
- rj=∑i∈Nin(j)dout(i)ri
- 임의 보행 관점에서 정의한 정산 분포 p :
- pj=∑i∈Nin(j)dout(i)pi
페이지랭크의 계산
페이지랭크의 계산: 반복곱
- 페이지랭크 점수의 계산에는 반복곱(power iteration) 을 사용한다
- 반복곱은 다음 세 단계로 구성된다
- 각 웹페이지 i의 페이지랭크 점수 ri(0)를 동일하게 웹페이지의수1 로 초기화한다
- 아래 식을 이용하여 각 웹페이지의 페이지랭크 점수를 갱신 한다
- rj(t+1)=∑i∈Nin(j)dout(i)r(t)
- 페이지랭크 점수가 수렴하였으면 종료하고 아닌 경우 두번째로 돌아간다
- 페이지랭크의 점수인 r(t)벡터와 r(t+1)벡터의 점수가 굉장히 유사한 경우에는 종류하고 아닌 경우에는 두번째 단계를 다시 수행한다
- 두 벡터의 값이 충분히 유사해지면 r(t+1) 값을 페이지랭크 값들의 벡터로 output으로 반환한다
- 반복곱 예시:
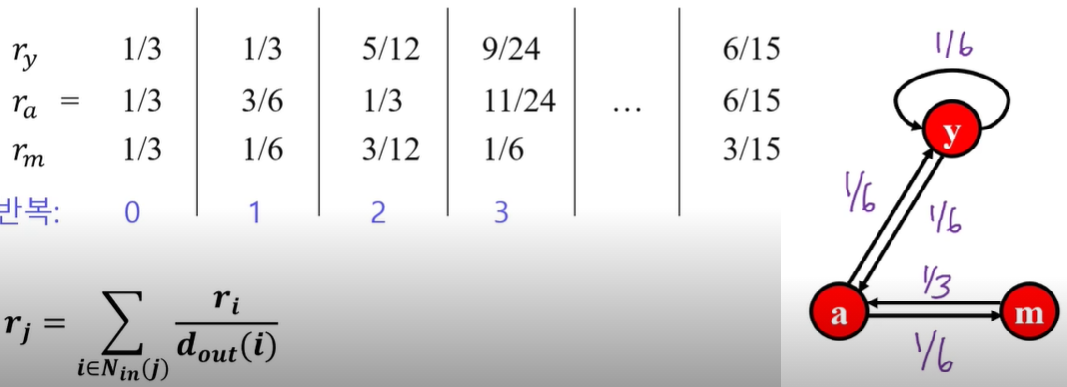
문제점과 해결책
- 반복곱이 항상 수렴하는 것은 보장할 수 없다
- 아래의 예시에서 페이지랭크 점수는 수렴하지 않는다

- 반복곱이 '합리적인' 점수로 수렴하는 것 또한 보장할 수 없다
- 아래의 예시에서 페이지랭크 점수는 0으로 수렴한다

- 위 문제를 해결하기 위해 순간이동(Teleport) 을 도입한다
- 임의 보행 관점에서, 웹을 서핑하는 웹서퍼의 행동을 다음과 같이 수정한다
- 현재 웹페이지에 하이퍼링크가 없다면(막다른 정점에 도달했다면), 임의의 웹페이지로 순간이동 한다
- 현재 웹페이지에 하이퍼링크가 있다면, 앞면이 나올 확률이 α인 동전을 던진다
- 앞면 이라면, 하이퍼링크 중 하나를 균일한 확률로 선택해 클릭한다
- 뒷면 이라면, 임의의 웹페이지로 순간이동 한다
- 첫번째와 4번재의 임의의 웹페이지는 전체 웹페이지들 중에 하나를 균일확률로 선택한다
- 순간이동에 의해서 스파이더 트랩 이나 막다른 정점 에 갇히는 일이 없어진다
- 𝛼를 감폭 비율(Damping Factor) 이라고 부르며 값으로 보통 0.8 정도를 사용한다
- 순간이동 도입은 페이지랭크 점수 계산을 다음과 같이 바꾼다
- 각 막다른 정점에서(자신을 포함) 모두 다른 정점으로 가는 간선을 추가한다
- 아래 수식을 사용하여 반복곱을 수핸한다
- rj=∑i∈Nin(j)(αdout(i)ri)+(1−α)∣V∣1
- ∣V∣ 는 전체 웹페이지의 수를 의미한다
- ∑i∈Nin(j)(αdout(i)ri) = 하이퍼링크를 따라 정점 j에 도착할 확률을 의미
- (1−α)∣V∣1 = 순간이동을 통해 정점 j에 도착할 확률을 의미
- 아래는 수정된 페이지랭크를 예시 그래프에 적용한 결과 :
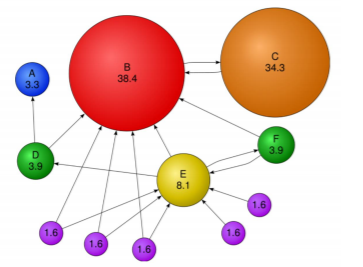
- 각 정점마다의 숫자는 페이지랭크 점수에 100을 곱한 숫자
- 정점 B 가 높은 페이지랭크 점수를 가진다
- 이것이 당연한 이유는 많은 정점으로 부터 투표를 받고 있다 (총 7개의 점점으로 부터 투표를 받는다)
- 투표를 받지 못하는 정점은 페이지랭크 점수가 낮다
- 그래도 0이 아닌 페이지랭크 값을 가지는 이유는 순간이동을 통해서 이 정점들에 도달할 확률들이 존재하기 때문이다
- 정점 C 라는 정점이 한개 밖에 들어오는 간선을 가지지 않았음에도 점수가 굉장히 높다
- 그 이유는 그 한개의 간선이 가장 페이지랭크 값이 높은 B로 부터 들어오기 때문이다
- 또한 정점 B는 자기가 가진 높은 페이지랭크 점수 전부를 정점 C에게 보내게 된다
- 즉, C 는 한표밖에 받지 못했지만 그 한표가 정말 신뢰하고 관련성이 높은 웹페이지로 부터 온 한표이기 때문에 페이지랭크 값이 높다






