머신러닝과 딥러닝, 가중치, 편향, 활성화 함수, 역전파에 대해 알아봅니다.
▶︎ 인공지능, 머신러닝, 딥러닝
🌟 인공지능(AI, Artificial Intelligence)
- 기계가 사람처럼 '지능적인' 행동을 하도록 만드는 기술 전체.
- 문제 해결, 학습, 추론, 판단 같은 사람의 지능 활동을 컴퓨터가 수행하게 하는 큰 개념
- 인공지능을 구현하는 방법으로 머신러닝과 딥러닝이 있다.
- 딥러닝은 머신러닝의 여러 방법 중 중요한 방법론.
🌟 머신러닝(기계학습, Machine Learning)
- 인공지능을 구현하는 방법 중 하나.
- 전통적인 프로그램: 사람이 모델을 만든다. (a 입력에 x조건이 성립하면 b를 출력하는 걸 인간이 작성)
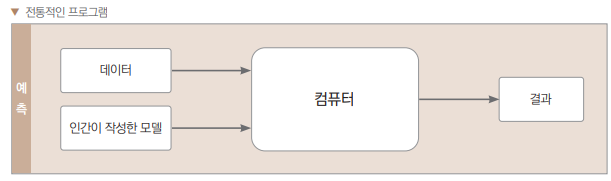
- 머신러닝: 컴퓨터가 데이터를 보고 알아서 모델을 만든다. (a입력에 출력이 b가 되는 조건x를 기계가 찾음)
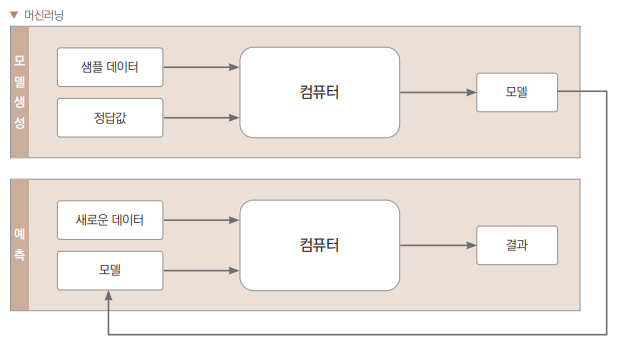
- step1) 입력값과 정답값 간의 관계를 찾아 머신러닝 알고리즘이 새로운 모델을 만든다. (데이터에서 스스로 패턴을 찾아 학습)
- step2) 그 학습 결과를 바탕으로 새로운 데이터가 주어졌을 때 결과를 예측/판단.
- 머신러닝을 수행하려면 많은 데이터가 필요.
🌟 딥러닝(Deep Learning)
- 인공 신경망을 기반으로 한 특수한 머신러닝 기법.
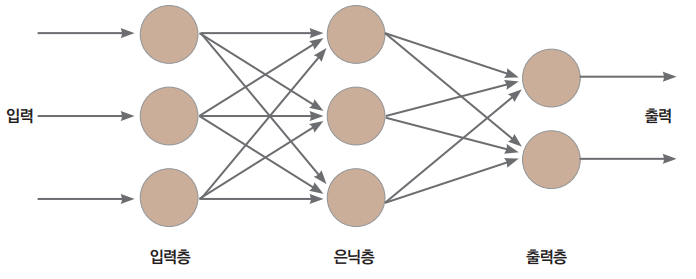
- 다른 여러개의 뉴런으로부터 입력값을 받아 일정 수준을 넘어서면 활성화 되어 출력값을 내보낸다.
- 입력층과 출력층 사이에 은닉층(보통 하나 이상의 수많은 은닉층이 존재)을 두어 인간의 신경망처럼 작동시킨다. ⇒ 다층 퍼셉트론 (MLP, multi-layer perceptron)
- 머신러닝과의 차이: 기계학습 시 입력값의 특징을 사람이 입력하지 않고, 기계가 직접 학습한다.
- 이미지 인식, 음성 인식, 자연어 처리 등에서 성능 좋음
- 다층 퍼셉트론의 한계
- 사라지는 경사도 vanishing gradient 문제
- 복잡한 문제 해결을 위해서는 신경망의 층수를 여러층 쌓은 모델을 이용해야 하는데,
- 깊은 층수를 쌓을수록 역전파 backpropagtion 학습과정에서 데이터가 사라져 학습이 잘 되지 않음
- +) 역전파(Backpropagation): 신경망에서 출력 값과 실제 값 사이의 차이를 계산하고, 오차를 줄이기 위해 출력부터 시작하여 역순으로 가중치를 조절하는 알고리즘
- 새로운 데이터를 잘 처리 못함.
- 사라지는 경사도 vanishing gradient 문제
- 한계의 극복
- pretraining: 깊은 층수의 신경망 학습 시 사전학습을 통해 학습 → vanishing gradient 문제 해결
- dropout: 학습도중 고의로 데이터를 누락 → 새로운 데이터 처리
+) 머신러닝 기법: 지도 학습, 비지도 학습, 강화 학습
1. 지도 학습 supervised learning
- 입력값과 결과값을 제공 → 이 둘의 관계를 분석하고 예측하는 모델을 만듦.
- 회귀: 예측 결과값이 연속성을 지니는 경우. 실수형으로 결과를 표현.
- 매출액 예측, 부동산 가격 예측, 거래량 예측
- 분류: 예측 결괏값이 비연속적인 경우. 범주형 값을 측정. ex) 예/아니오 결과.
- 이때 얻을 수 있는 분류 종류를 클래스class라고 한다. 클래스가 2개뿐일 때 이진분류라고 한다.
+) 머신러닝에서 얻고자 하는 결괏값을 목적값 또는 타깃값이라고 합니다.
2. 비지도 학습 unsupervised learning
- 정답이 없는 데이터만으로 학습. 정답이 제공되지 않고 입력값만을 이용한 학습.
- 군집화 clustering: 비슷한 데이터끼리 묶기.
- 변환 transformation: 목적에 따라 데이터를 다른 형태로 변환.
- 연관 association: 장바구니 분석.
3. 강화 학습 reinforcement learning
- 결과값 대신 reward가 주어짐. (행동에 대한 보상/처벌)
+) 딥러닝은 그럼 어디에 속하지?
- 딥러닝은 특정한 하나의 모델이라기 보다는 머신러닝에 속하는 대표적인 방법론으로 → 지도학습, 비지도학습, 강화학습 모두에 이용될 수 있다.
- 예) 딥러닝에 지도학습 적용, 딥러닝에 비지도 학습 적용, 딥러닝에 강화학습 적용
▶︎ 머신러닝의 한계와 딥러닝
머신러닝의 한계
: 불규칙하게 분포하는 데이터 분류의 어려움
- 규칙(수식)을 만들어 놓고 새로운 사례의 변수들을 입력하면 변수의 값에 따라 결과가 위치한다. 그 위치가 선이나 평면을 경계로 어디에 속하는지 보고 추론한다.
- ex) 증상으로 병명을 추론하는 문제에서
- 변수(증상)는 좌표축에서 하나의 차원.
- 같은 병명의 환자들은 각 변수(증상)가 비슷하니 n차원 공간에서 비슷한 위치에 뭉쳐있다.
- 이를 잘 구분할 수 있는 어떤 규칙을 만들 수 있다. (2차원이라면 뭉쳐있는 두 집단을 구분하는 선)
- 새로운 사례가 발생하면 → 사례의 변수들이 입력해 그 값의 위치를 보고 → 만들어놓은 규칙을 기준으로 어디에 속하는지 판단한다.
- 기존 데이터를 분류하는 규칙을 잘 만들어야 새로운 사례에 대해 잘 판단하고 추론할 수 있다.
- 그런데 실제 데이터는 잘 분류하기 쉽지 않다. 기존데이터를 잘 분류할 수 없음. → 새로운 사례가 입력되면 버벅된다.
좌표 평면을 왜곡시키는 다층 신경망
- 2차원 공간에 데이터가 분포한다면, 어떤 선(일차식)을 그어 분류해 볼 수 있다.
- 하지만 선으로는 데이터를 완벽하게 분류하지는 못한다.
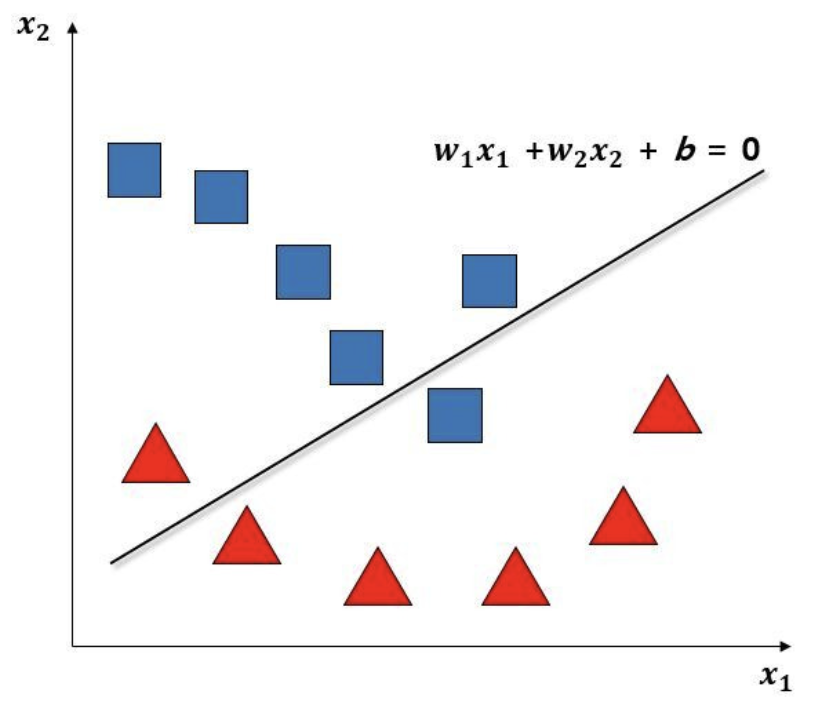
- 하지만 선으로는 데이터를 완벽하게 분류하지는 못한다.
- 신경망 모델처럼 분류해 본다면?
- 출력값을 만드는 f(x) = w1x1 + w2x2 + b → 위의 방법의 결과와 다를게 없음.
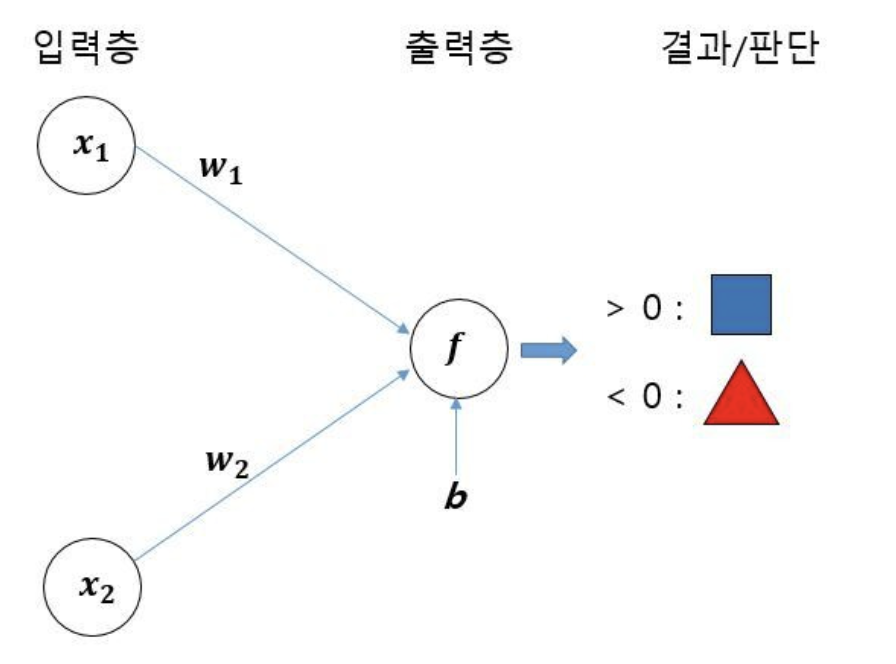
- 하지만 은닉층을 추가하면…! (다층 신경망을 만들기)
- 기존 데이터가 분포하던 좌표평면이 데이터를 분류하기 좋게 왜곡되는 효과 발생!
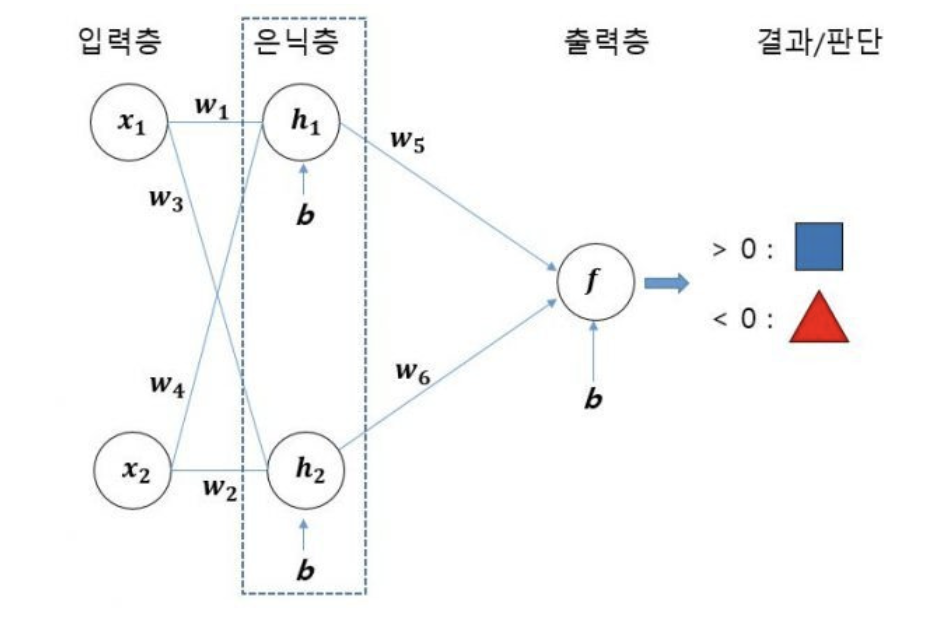
- 층을 늘릴수록 복잡한 왜곡이 생긴다.
- 무질서하게 흩어져 있는 데이터를 더 잘 분류할 수 있게 된다.
- 층을 많이 두는 방식: deep learning
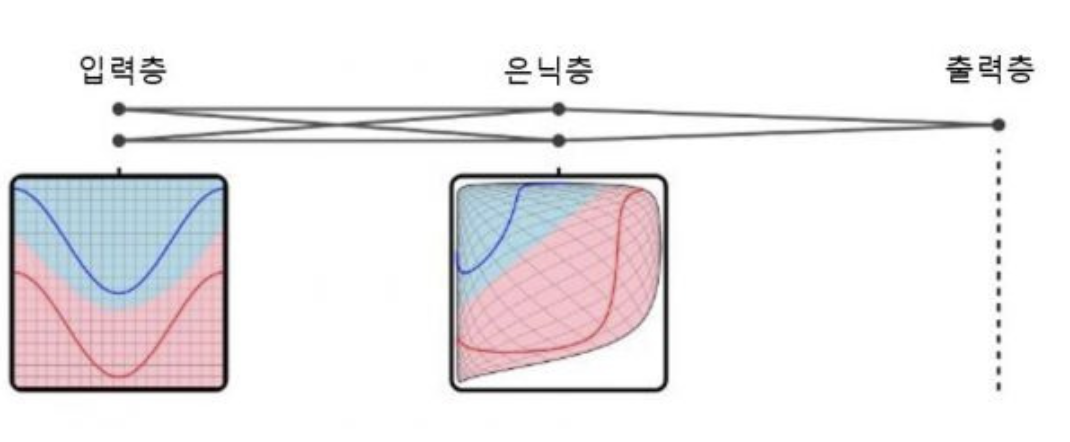
+) 왜 은닉층을 거치면 왜곡 효과가 나타나지?
▶︎ 딥러닝: 가중치, 편향, 활성화 함수, 역전파
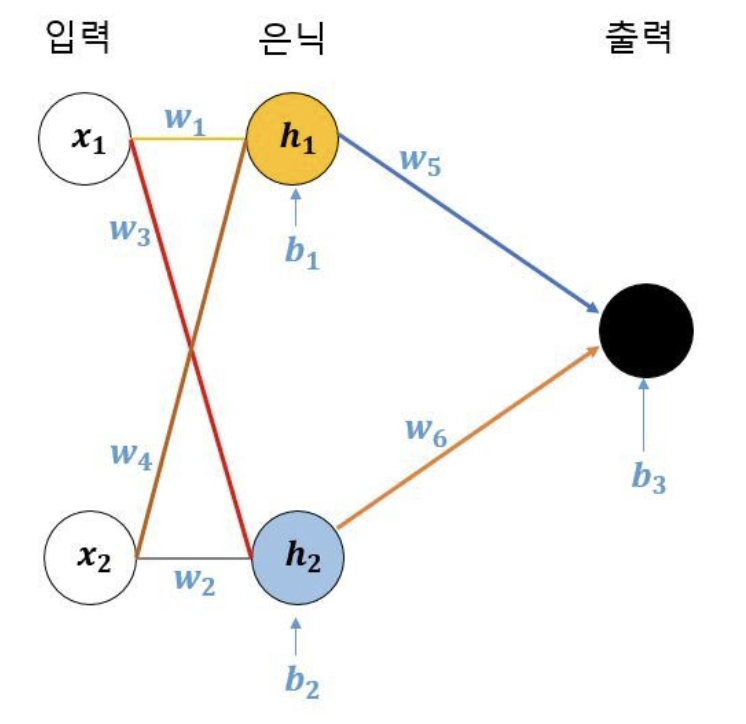
신경망 구성 요소
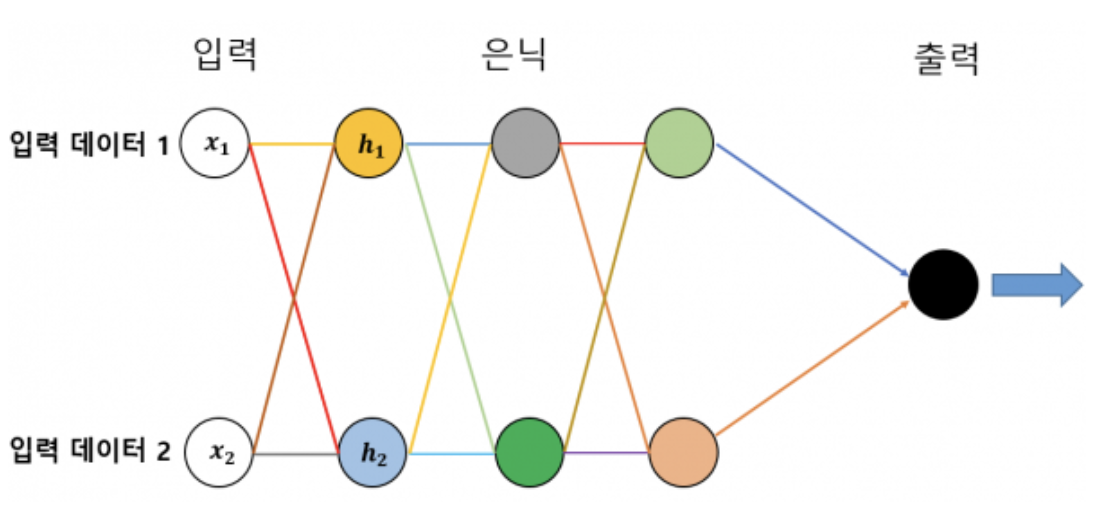
- 원: 하나의 뉴런.
- 뉴런을 연결하는 선: 데이터가 왼쪽에서 오른쪽 방향의 뉴런으로 전달된다.
- x1은 h1으로도 h2로도 전달된다. (x2도)
- 하지만 x1은 각기 다른 값으로 h1 과 h2로 전달된다.
- 처음 입력된 데이터들이 계속 다른 값으로 변하면서 뉴런에서 뉴런을 거쳐 출력층으로 나아간다.
뉴런(Perceptron)의 구성 요소
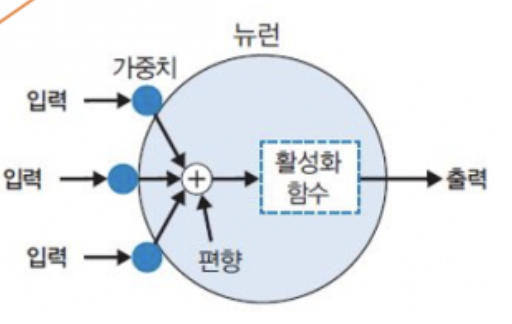
가중치 weight
- 입력값에 대해 다르게 곱해지는 수치.
- x1이 각기 다른 값으로 h1과 h2로 전달되었다. 같은 x1에 대해 가중치가 다르기 때문.
편향 bias
- 하나의 뉴련으로 입력된 모든 값을 다 더한 다음 (가중합) 이 값에 더해주는 상수.
- 이 값은 하나의 뉴런에서 활성화 함수를 거쳐 최종적으로 출력되는 값을 조절.
- 편향은 임계점을 얼마나 쉽게 넘을지 말지를 조절해주는 값.
- 가중합 ( = 입력값1 가중치1 + 입력값2 가중치2 + 입력값3 * 가중치3 … ) + 편향
활성화 함수
- 뇌의 뉴런: 한 뉴런에서 역치를 넘으면 다른 뉴런으로 신호를 전달한다.
- 인공신경망: 임계점을 설정하고, 출력값에 변화를 주는 함수를 이용(활성화 함수).
- 입력과 가중치의 곱을 모두 합산한 후, 그 결과를 활성화 함수에 전달. 활성화 함수는 이 값을 이진 출력(0 또는 1)으로 변환.
- sigmoid 함수, ReLU 렐루 함수, 항등 함수, 소프트 맥스 등 종류 많음.
- 활성화 함수로 인해 은닉층으로 인한 좌표평면 왜곡 효과가 발생.
그럼 가중치와 편향은 어떻게 구해? → 역전파를 통해!
- 기존 데이터를 학습해서 가장 적절한 값들을 찾아내야 한다.
- 성능이 좋은 딥러닝을 구축하는 것은 결국 이 수치들의 최적값을 구해야 하는 것.
- 처음에는 최적의 가중치와 편향을 모르니 임의로 설정.
- 출력값과 실제값(정답)의 차이를 보고 가중치와 편향을 다른 값으로 바꾸며 조절.
- 차이는 (출력값 - 실제값)² 으로 표현 ⇒ 손실 함수라고 한다.
- 아예 다른 가중치와 편향을 임의로 설정하는 방법이 있지만, 뉴런의 수가 많은 경우에는 경우가 무한대라 → 처음 설정한 가중치와 편향을 조금씩, 계속 개선한다.
- 아주 작은 w5의 변화량에 따른 (출력값 - 실제값)²의 변화량 = (출력값 - 실제값)²를 w5로 미분한 값
- 새로운 w5 = 이전 w5 - ((출력값 - 실제값)²를 w5로 미분한 값)
- 새로운 w5를 구한 것처럼 신경망을 구성하는 모든 가중치와 편향을 위의 방식(출력값과 실제값의 차이를 조금 줄이는 방식)으로 오른쪽(출력층) 에서 왼쪽(입력층) 방향으로 역방향으로 하나씩 수정한다.
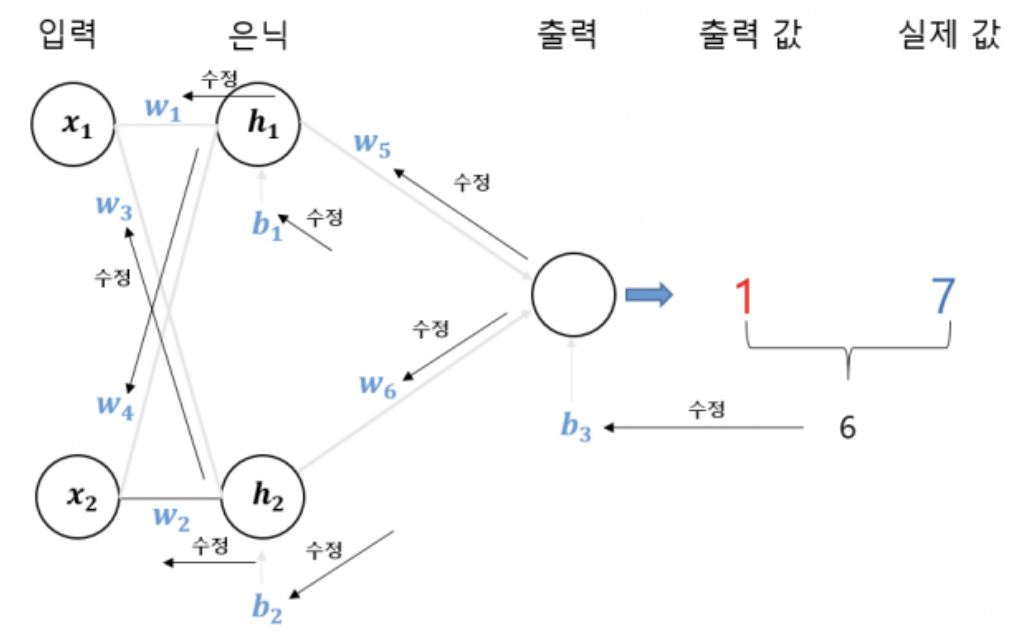
- 조금 개선한 신경망으로 새로운 출력값을 구하고, 다시 실젯값과 차이를 구한 다음 이 차이를 또 줄이도록 모든 가중치화 편향을 조금씩 수정한다. 반복하면서 최적화된 가중치와 편향 값을 구한다.
- ⇒ 역전파 backpropagation, 오차의 역전파
+) 그럼 처음에 임의로 설정되는 가중치와 편향 값은 랜덤인가?
뉴런(Perceptron)의 동작 과정
- (1) 입력 벡터와 가중치 벡터의 내적을 계산. ( 각각 곱해서 더한다.)
- 입력: x = [x₁, x₂, x₃]
가중치: w = [w₁, w₂, w₃] - 내적: x·w = x₁w₁ + x₂w₂ + x₃w₃
- 입력: x = [x₁, x₂, x₃]
- (2) 계산된 값에 편향을 더한다.
- (3) 그 결과를 활성화 함수에 전달하여 최종 출력을 계산.
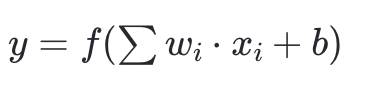
참고)