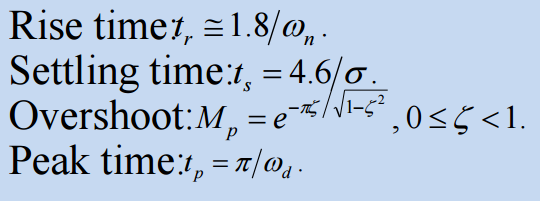시스템이 어떻게 움직이는지를 알아보도록 하자
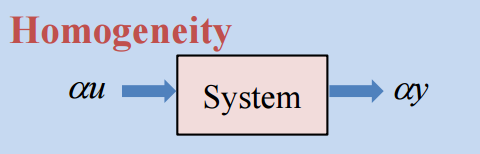
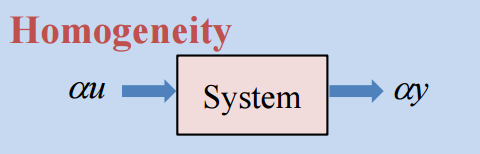
Linearity
학부 수준에서 제어공학이 잘 이루어 지려면 선형시스템에 대해서 많이 이야기 한다.
입력에 α {\alpha} α α {\alpha} α
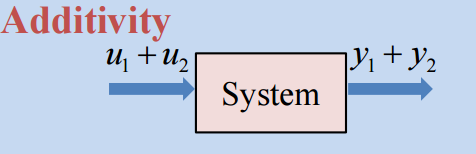
입력에 u 1 , u 2 {u}_{1}, {u}_{2} u 1 , u 2 y 1 , y 2 {y}_{1}, {y}_{2} y 1 , y 2
위 Homogenity와 Additivity 둘다 만족하는 상황을 Principle of Superposition이라 한다. 선형 시스템은 Principle of Superposition을 만족한다.
Time Invariance
시간이 지남에 따라도 변하지 않는 것을 의미한다.
Philosophy는 Principle of Superposition에서 기본적인 입력(impulse, exponential, etc)에 대한 기본적인 응답을 사용하여 시스템의 응답을 찾아내는 것이다.
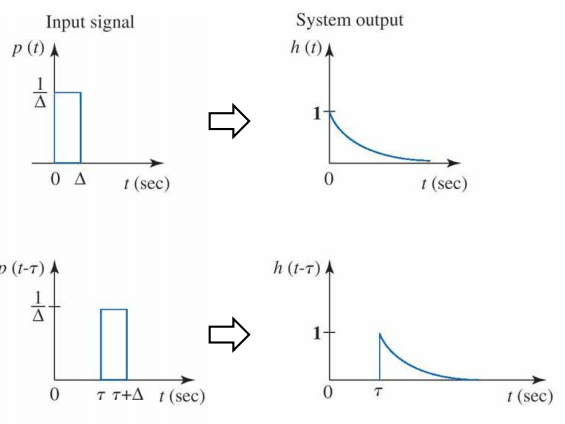
Linearity : i n p u t u 1 ( t ) = u ( 0 ) p ( t ) → o u t p u t y 1 ( t ) = u ( 0 ) h ( t ) input\;{u}_1(t)=u(0)p(t) \rightarrow output\;y_1(t)=u(0)h(t) i n p u t u 1 ( t ) = u ( 0 ) p ( t ) → o u t p u t y 1 ( t ) = u ( 0 ) h ( t )
Time Invariance : i n p u t u 2 ( t ) = p ( t − τ ) → o u t p u t y 1 ( t ) = h ( t − τ ) input\;{u}_2(t) = p(t-\tau) \rightarrow output\;y_1(t)=h(t-\tau) i n p u t u 2 ( t ) = p ( t − τ ) → o u t p u t y 1 ( t ) = h ( t − τ )
Response by Convolution
LTI시스템에서 입출력은 Convolution integral로 연결된다.
Transfer Functions and Frequency Response
출력 H ( j ω ) H(j\omega) H ( j ω ) M ( ω ) = ∣ H ( j ω ) ∣ M(\omega)=|H(j\omega)| M ( ω ) = ∣ H ( j ω ) ∣ ϕ ( ω ) = ∠ H ( j ω ) \phi(\omega)=\angle H(j\omega) ϕ ( ω ) = ∠ H ( j ω )
Time Delay
L { f ( t − λ ) } = e − s λ F ( s ) , λ > 0 L\{f(t-\lambda)\}=e^{-s\lambda}F(s), \lambda > 0 L { f ( t − λ ) } = e − s λ F ( s ) , λ > 0 e − s λ e^{-s\lambda} e − s λ
Poles and Zeros
일반적인 Trnasfer Function은 다음과 같은 형태를 지니게 된다.
H ( s ) = b 1 s m + b 2 s m − 1 + ⋯ + b m + 1 s n + a 1 s n − 1 + ⋯ + a n H(s) = \frac{b_1s^m+b_2s^{m-1}+\cdots+b_{m+1}}{s^n+a_1s^{n-1}+\cdots+a_n} H ( s ) = s n + a 1 s n − 1 + ⋯ + a n b 1 s m + b 2 s m − 1 + ⋯ + b m + 1
Impulse Response
h ( t ) = L − 1 { H ( s ) } = L − 1 K Π i = 1 m ( s − z i ) Π i = 1 n ( s − p i ) = n a t u r a l r e s p o n s e h(t) = L^{-1}\{H(s)\}=L^{-1}K\frac{\Pi^{m}_{i=1}(s-z_i)}{\Pi^{n}_{i=1}(s-p_i)} = natural\;response h ( t ) = L − 1 { H ( s ) } = L − 1 K Π i = 1 n ( s − p i ) Π i = 1 m ( s − z i ) = n a t u r a l r e s p o n s e The Block Diagram
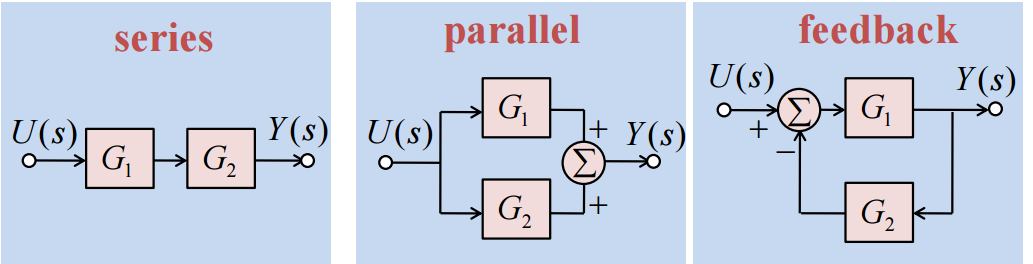
블록 다이어 그램은 시스템의 요소들 사이의 관계를 그림으로 나타낸 형식을 말한다.
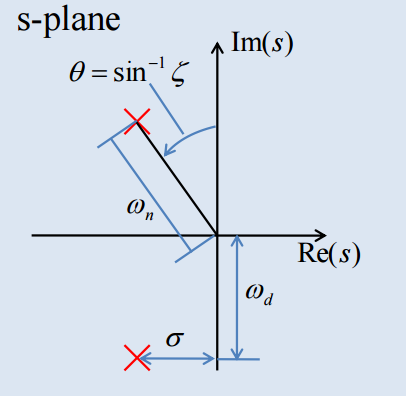
Effect of Pole Locations
Complex poles : s = − σ ± j ω d s=-\sigma \pm j\omega_d s = − σ ± j ω d a ( s ) = ( s + σ − j ω d ) ( s + σ + j ω d ) = ( s + σ ) 2 + ω d 2 a(s)=(s+\sigma-j\omega_d)(s+\sigma+j\omega_d)=(s+\sigma)^2+\omega_d^2 a ( s ) = ( s + σ − j ω d ) ( s + σ + j ω d ) = ( s + σ ) 2 + ω d 2
Related transfer function :H ( s ) = ω n 2 ( s + σ ) 2 + ω d 2 = ω n 2 s 2 + 2 ζ ω n s + w n 2 H(s)=\frac{\omega^2_n}{(s+\sigma)^2+\omega_d^2}=\frac{\omega^2_n}{s^2+2\zeta\omega_ns+w^2_n} H ( s ) = ( s + σ ) 2 + ω d 2 ω n 2 = s 2 + 2 ζ ω n s + w n 2 ω n 2 σ : = ζ ω n , ω d : = ω 1 − ζ 2 \sigma:=\zeta\omega_n, \; \omega_d:=\omega\sqrt{1-\zeta^2} σ : = ζ ω n , ω d : = ω 1 − ζ 2
ζ = σ ω n : = d a m p i n g r a t i o \zeta=\frac{\sigma}{\omega_n}:=damping\;ratio ζ = ω n σ : = d a m p i n g r a t i o θ \theta θ 30 ° 30\degree 3 0 ° θ = ζ \theta = \zeta θ = ζ ω n : = u n d a m p e d n a t u r a l f r e q u e n c y → \omega_n:=undamped\;natural\;frequency \rightarrow ω n : = u n d a m p e d n a t u r a l f r e q u e n c y → ω d : = d a m p e d n a t u r a l f r e q u e n c y \omega_d:=damped\;natural\;frequency ω d : = d a m p e d n a t u r a l f r e q u e n c y
Impulse response : h ( t ) = ω n 1 − ζ 2 e − σ t ( s i n ω d t ) 1 ( t ) h(t)=\frac{\omega_n}{\sqrt{1-\zeta^2}}e^{-\sigma t}(sin\omega_dt)1(t) h ( t ) = 1 − ζ 2 ω n e − σ t ( s i n ω d t ) 1 ( t ) ζ \zeta ζ
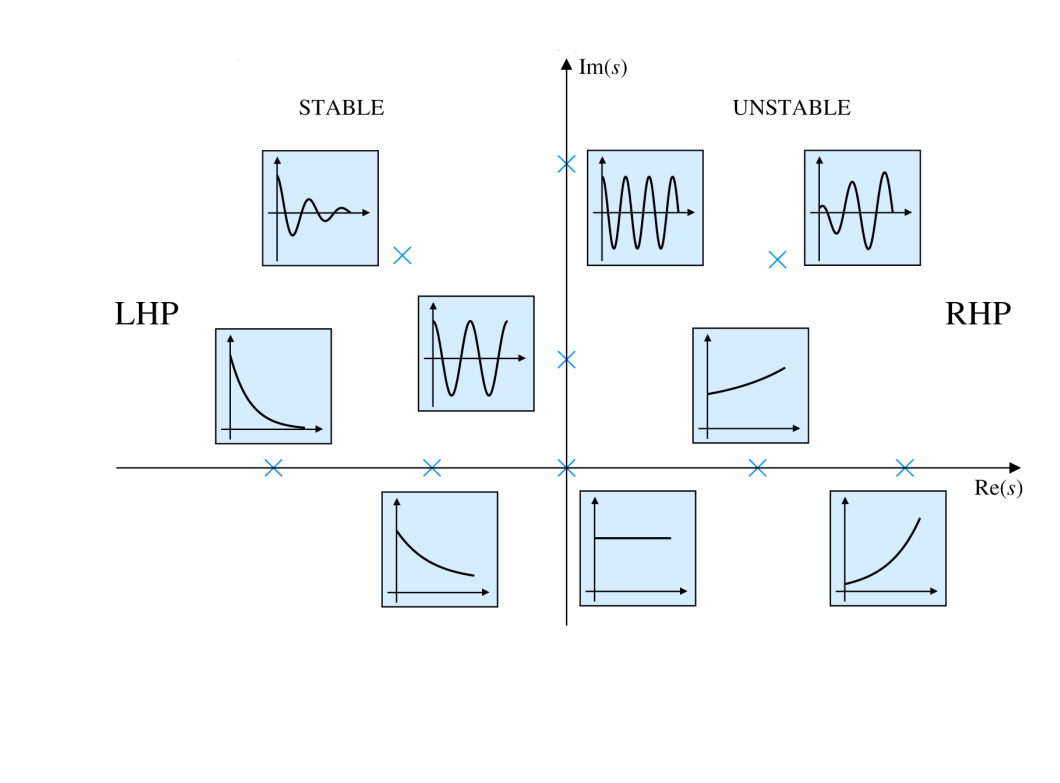
Stability of complex poles
(Complex polse : s = − σ ± j ω d s=-\sigma\pm j\omega_d s = − σ ± j ω d { σ < 0 : u n s t a b l e σ = 0 : n e u t r a l l y s t a b l e σ > 0 : s t a b l e \begin{cases}\sigma < 0:unstable\\\sigma=0:neutrally\;stable\\\sigma>0:stable\end{cases} ⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ σ < 0 : u n s t a b l e σ = 0 : n e u t r a l l y s t a b l e σ > 0 : s t a b l e
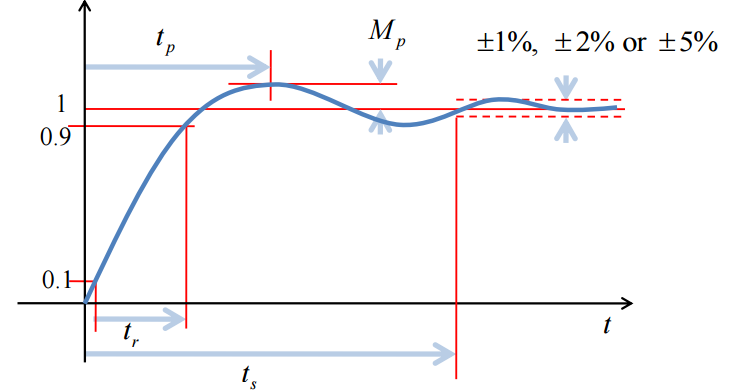
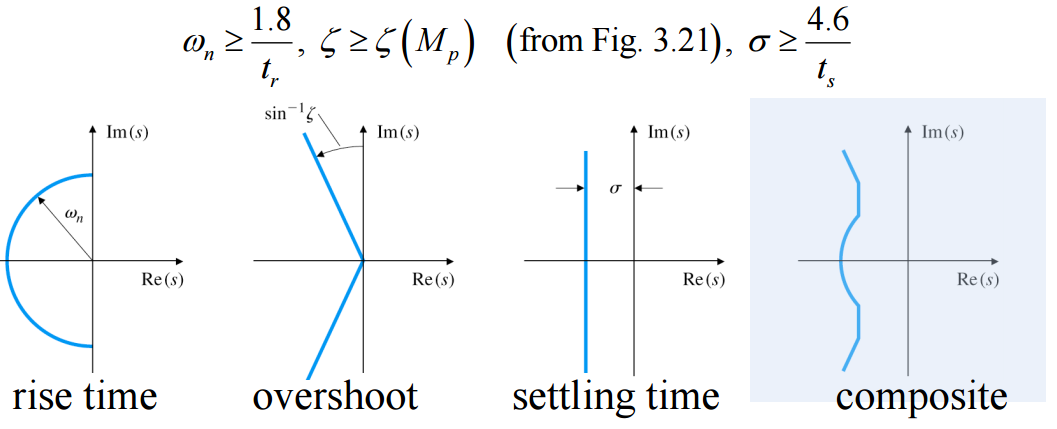
Time-Domain Specifications
Rise time t r t_r t r t s t_s t s M p M_p M p
Time-domain specifications for second order system
H ( s ) = w n 2 s 2 + 2 ζ ω n s + ω n 2 H(s) = \frac{w_n^2}{s^2+2\zeta\omega_ns+\omega^2_n} H ( s ) = s 2 + 2 ζ ω n s + ω n 2 w n 2
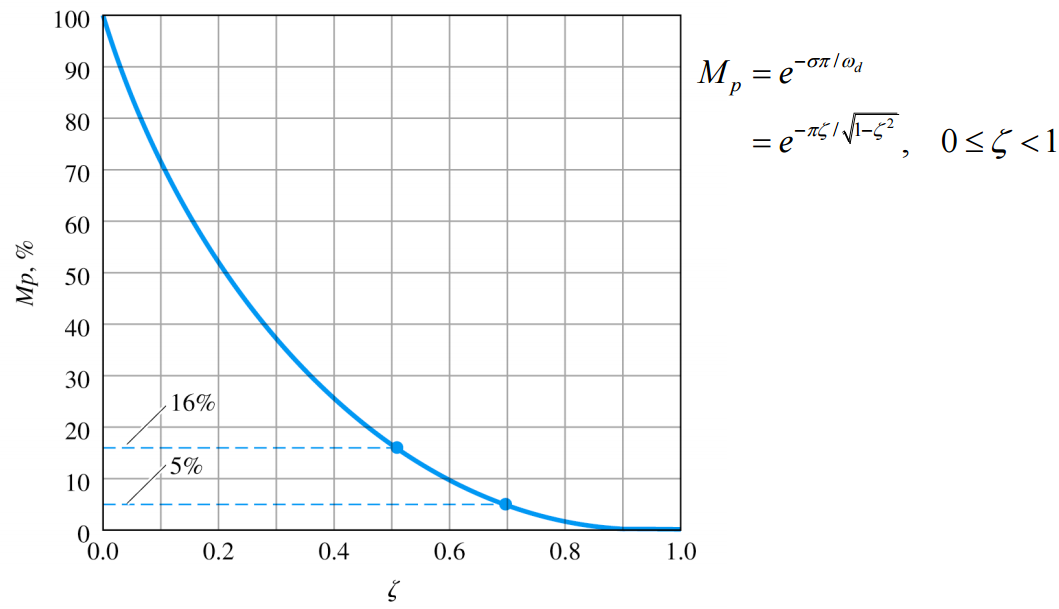
Overshoot and damping ratio
시스템의 응답을 제어기를 통해 바꾸고자 할 때, 파형의 형태를 디자인 할 수 있다.
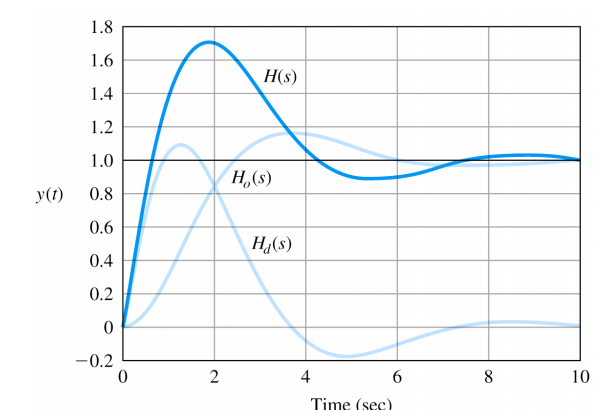
Effect of Zeros and Additional Poles
Pole 근처에 Zero가 위치하게 된다면 그곳과 관련된 natural response 작아지게 된다.
ex)
Pole이 2개있고 Zero가 하나있는 시스템에 대해서 알아보자
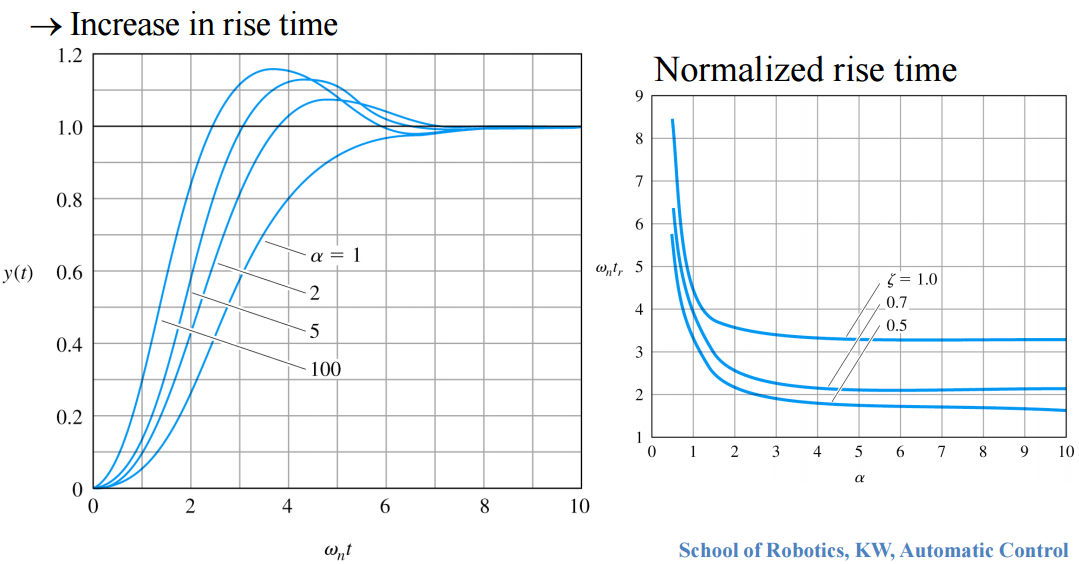
H 1 ( s ) = ( s / α ζ ω n ) + 1 ( s / ω n ) 2 + 2 ζ ( s / ω n ) + 1 H_1(s)=\frac{(s/\alpha\zeta\omega_n)+1}{(s/\omega_n)^2+2\zeta(s/\omega_n)+1} H 1 ( s ) = ( s / ω n ) 2 + 2 ζ ( s / ω n ) + 1 ( s / α ζ ω n ) + 1 Z e r o : − α ζ ω n = − α σ : { α ≫ 0 ( l i t t l e i n f l u e n c e ) α ≅ 1 ( s u b s t a n t i a l i n f l u e n c e ) Zero : -\alpha\zeta\omega_n = -\alpha\sigma : \begin{cases} \alpha\gg0\;(little\;influence)\\\alpha\cong1\;(substantial\;influence) \end{cases} Z e r o : − α ζ ω n = − α σ : { α ≫ 0 ( l i t t l e i n f l u e n c e ) α ≅ 1 ( s u b s t a n t i a l i n f l u e n c e )
Overshoot M p M_p M p α \alpha α
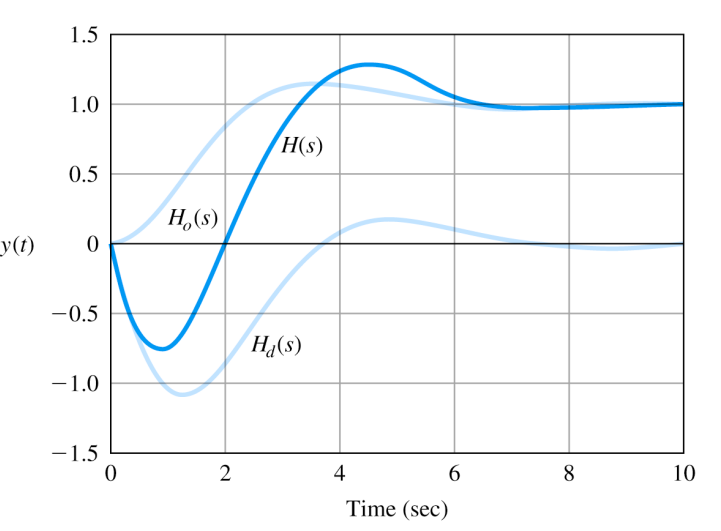
α > 0 \alpha > 0 α > 0 α < 0 \alpha < 0 α < 0
H ( s ) = 1 ( s / α ζ ω n + 1 ) [ ( s / ω n ) 2 + 2 ζ ( s / ω n ) + 1 ] H(s)=\frac{1}{(s/\alpha\zeta\omega_n+1)[(s/\omega_n)^2+2\zeta(s/\omega_n)+1]} H ( s ) = ( s / α ζ ω n + 1 ) [ ( s / ω n ) 2 + 2 ζ ( s / ω n ) + 1 ] 1 α \alpha α
Stability
제어에서 가장 중요한 부분이 된다.
이때, Pole에 실수 측이 없고 허수 측만 존재한다면 시스템은 진동하게 된고 이를 oscillatory system이라 부른다.
유한한 입력이 들어왔을때, 유한한 출력이 나오게 된다면 이는 bounded input-bounded output(BIBO) stability라 한다.h ( t ) h(t) h ( t ) ∫ − ∞ ∞ ∣ h ( τ ) d τ ∣ < ∞ \int_{-\infty}^{\infty}|h(\tau)d\tau|<\infty ∫ − ∞ ∞ ∣ h ( τ ) d τ ∣ < ∞

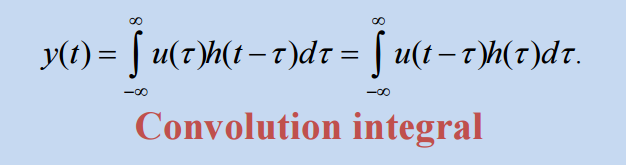
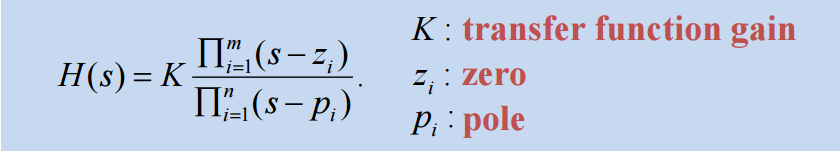
 가 커지면 커질수록 진동의 감속이 더 빨라진다.
가 커지면 커질수록 진동의 감속이 더 빨라진다.