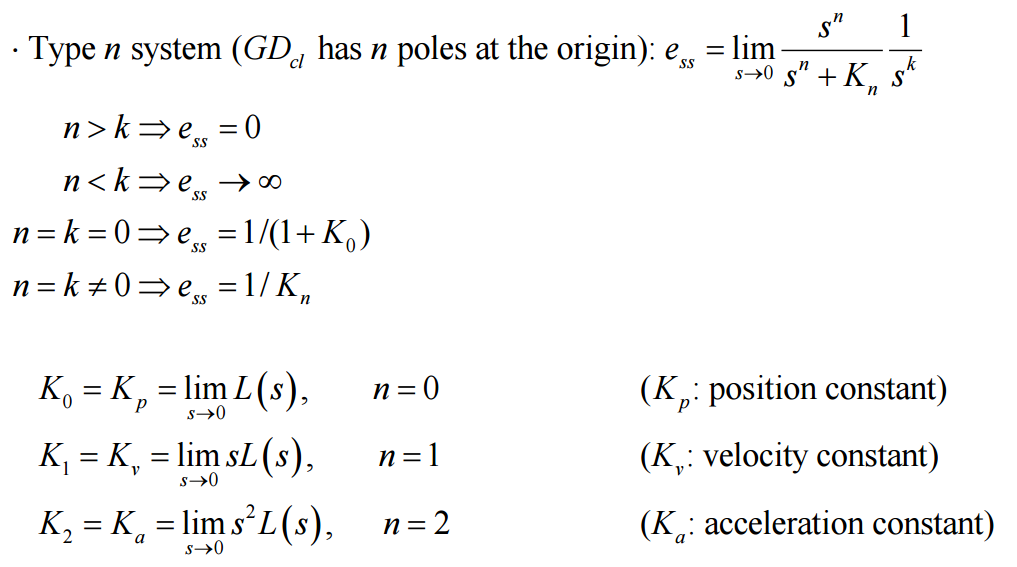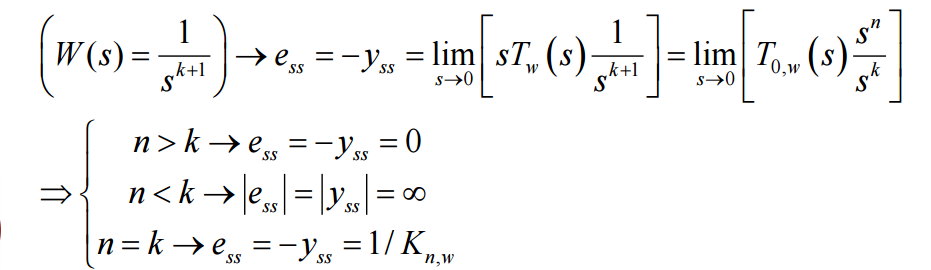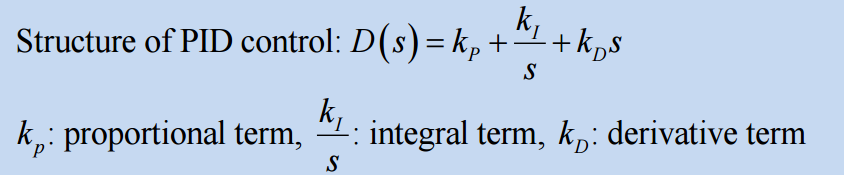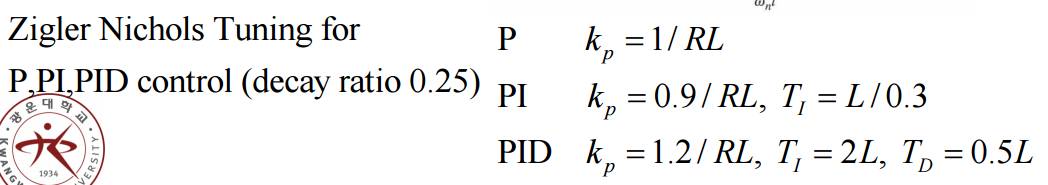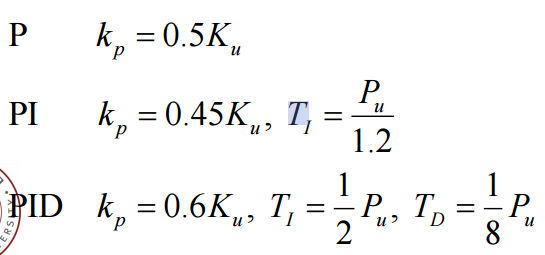자동제어 - Analysis of Feedback

Basic Equations of Control

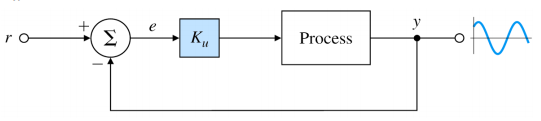
Open-loop control system

Open-loop system의 출력은 다음과 같다.
$Y_{ol}=GD_{ol}R+GW$
출력과 Reference간의 오차는 다음과 같다.
$\begin{aligned}E_{ol} &= R-Y_{ol} \\ &= R-[GD_{ol}R+GW]\\ &= [1-GD_{ol}]R-GW\\ &= [1-T_{ol}]R-GW\end{aligned}$

Feedback control system with disturbance and noise

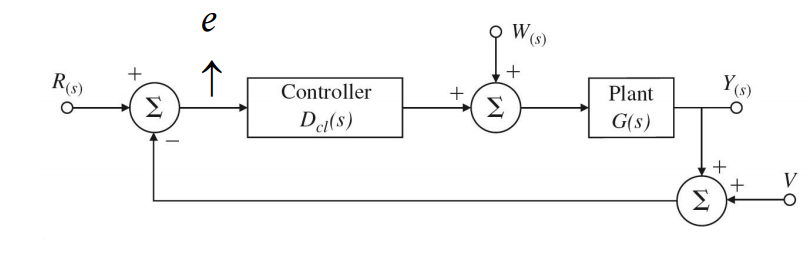
여기서 $V$는 sensor noise를 의미한다.
Feedback control의 출력은 다음과 같다.
$Y_{cl}=\frac{GD_{cl}}{1+GD_{cl}}R+\frac{GD_{cl}}{1+GD_{cl}}W-\frac{GD_{cl}}{1+GD_{cl}}V$
$U=\frac{D_{cl}}{1+GD_{cl}}R-\frac{GD_{cl}}{1+GD_{cl}}W-\frac{D_{cl}}{1+GD_{cl}}V$
출력과 Reference간의 오차는 다음과 같다.
$E_{cl}=\frac{1}{1+GD_{cl}}R-\frac{G}{1+GD_{cl}}W+\frac{GD_{cl}}{1+GD_{cl}}V$

Stability

Open loop systems

open loop system에서 stable하려면은 plant와 controller의 pole이 모두 LHP에 있어야 한다.
그렇다면 unstable한 pole을 RHP의 zero로 없앨 수 있을까?

noise나 disturbance와 같이 unstable한 pole의 위치를 정확히 알지 못한다면, 그 근처에 zero가 있어 영향이 적다고 하더라도 시간이 지남에
따라 영향을 받을 정도로 값이 커지게 되어 결국 unstable해지게 된다.

Feedback systems

System의 pole은 $1+GD_{cl}=0$이다.
이때, $G(s)=\frac{b(s)}{a(s)},\;D_{cl}(s)=\frac{c(s)}{d(s)}$이라면, system의 pole은 $a(s)d(s)+b(s)c(s)=0$가 되어 unstable한 pole이 존재하더라도 stable하게 만들 수 있다.

Tracking

Tracking problem은 output이 reference input을 가능한 가깝게 쫓아가는 것을 말한다.

Open-loop case

• plant가 stable한 상태에서 고려한다.
• controller가 proper(분모의 차수가 분자보다 높은 경우)해야한다.
• controller가 너무 빠르거나 큰 입력을 받으면 안된다.
• sensitivity problem(stable한 pole이 허수축에 가까운 경우)

Feedback을 사용하여 만들 수 있다.

Regulation

Regulation problem은 reference가 상수이고 disturbance의 영향을 없애면서 오차를 작게 유지하는 것이다.

Open-loop case : controller가 disturbance에 영향을 줄 수 없다.

Feedback case : disturbance와 noise간의 적절한 구간을 찾아 controller를 조절할 수 있다. 이때, disturbance는 low frequency에서 크고, noise는 high frequency에서 크다. 따라서, low frequency 영역에서는 disturbance를 줄이는 방향으로 가고 high frequency에서는 noise를 줄이는 방향으로 간다.

Sensitivity

plant gain이 $G\rightarrow G+\delta G$로 바뀌었을 때

Open-loop : (Steady-state gain : $T_{ol}=GD_{ol}$)
$T_{ol}+\delta T_{ol}=D_{ol}(G+\delta G)=D_{ol}G+D_{ol}\delta G=T_{ol}+D_{ol}\delta G$
여기서 Normailized error 는 다음과 같다.
$\frac{\delta T_{ol}}{T_{ol}}=\frac{D_{ol}\delta G}{D_{ol}G}=\frac{\delta G}{G}$

Sensitivity는 $G$가 1%바뀔 때 $T_{ol}$이 몇 %바뀌는 지를 의미한다.
$\rightarrow \frac{fractional\;change\;in\;T_{ol}}{fractional\;change\;in\;G}\rightarrow S^T_G=\frac{\frac{\delta T_{ol}}{T_{ol}}}{\frac{\delta G}{G}}$

따라서 open loop system에서는 plant의 전달함수가 1% 바뀌면 전체 전달함수도 1% 바뀐다.

Feedback case :

• steady-state gain : $T_{cl}+\delta T_{cl} = \frac{(G+\delta G)D_{cl}}{1+(G+\delta G)D_{cl}},\;T_{cl}=\frac{GD_{cl}}{1+GD_{cl}}$
• 1st-order variation : $\delta T_{cl}=\frac{dT_{cl}}{dG}\delta G$
  $\frac{\delta T_{cl}}{T_{cl}}=\frac{1}{T_{cl}}\frac{dT_{cl}}{dG}\delta G = (\frac{G}{T_{cl}}\frac{dT_{cl}}{dG})\frac{\delta G}{G}=(sensitivity)\frac{\delta G}{G}$

따라서, Plant의 전달함수에 따른 $T_{cl}$의 sensitivity는 다음과 같다.
$S^{T_{cl}}_G := \frac{G}{T_{cl}}\frac{dT_{cl}}{dG}$

$D_{cl}(or\;GD_{cl})$이 적당히 크다면은 plant의 sensitivity는 변하지 않는다.

Control of Steady-State Error : System Type

Steady-state system error가 0 이 아닌 유한한 상수일 때 polynomial reference input의 Degree를 System Type이라 부른다.

System Type for Reference Tracking

• Type 0 system ($GD_{cl}의\;pole이\;원점에\;없을\;때$) : $G(0)D_{cl}(0)=K_p,\;R(s)=1/s$
  $\rightarrow e_{ss}=\lim_{s\rightarrow0}s\frac{1}{1+GD_{cl}}\frac{1}{s}=\frac{1}{1+GD_{cl}(0)}$
• Type n system ($GD_{cl}의\;pole이\;원점에\;n개\;있을\;때$) : $GD_{cl}(s)=\frac{GD_{clo(s)}}{s^n},\;GD_{clo}(0)=K_n$
  $e_{ss}=\lim_{s\rightarrow0}s\frac{1}{1+\frac{GD_{clo}(s)}{s^n}}\frac{1}{s^{k}}=\lim_{s\rightarrow 0}\frac{s^n}{s^n+K_n}\frac{1}{s^k}$

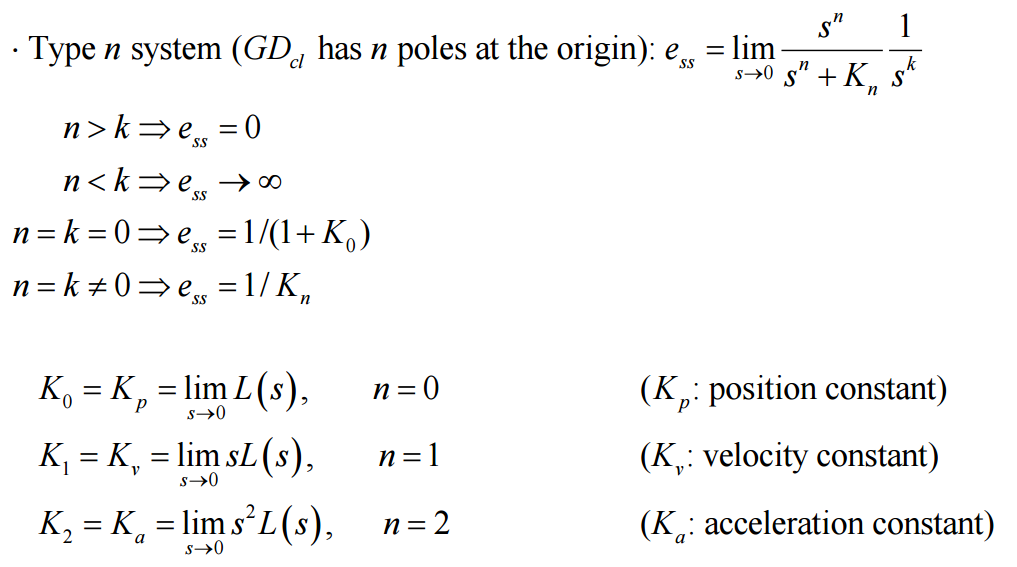
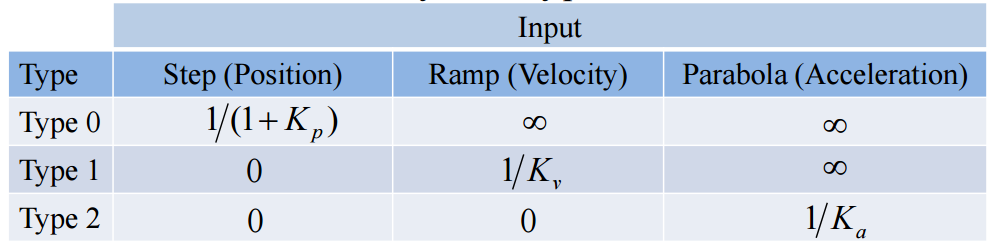
System Type : Regulation and Disturbance Rejection

Disturbance또한 Reference때와 비슷하게 $w(t)=\frac{t^k}{k!}$의 형식으로 나타냈을 때로 가정한다. 이때, Reference와 noise는 0이다.

Disturbance Rejection에서는 Reference때와는 다르게 Controller의 pole이 원점에 몇개 있는지로 확인한다.

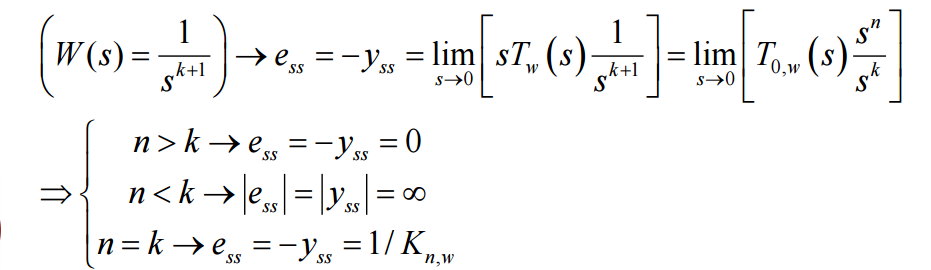
The Three-Trem Controller : PID Control

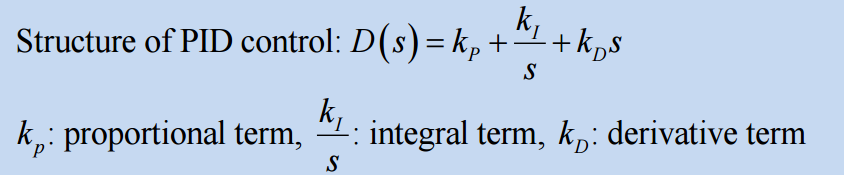
Proportional Control (P)

$u=k_pe, \frac{U(s)}{E(s)}=D_{cl}(s)=k_p$
이때, plant는 2nd order form $G(s)=\frac{A}{s^2+a_1s+a_2}$이라고 하자.
Closed-loop characteristic equation :

이를 통해 2nd order form에서 상수항을 변화 시킬 수 있다는 것을 알 수 있다. 이는 natural frequency를 바꿀수 있으며, 이를 통해 감쇠비 또한 조절 할 수 있다. natural frequency가 커지면 감쇠비는 작아진다. 따라서 크게 진동하게 된다.

Proportional plus Integral Control (PI)

$u(t)=k_pe(t)+k_I\int^t_te(\tau)d\tau\\\frac{U(s)}{E(s)}=D_{cl}=k_p+\frac{k_I}{s}$
Integral term은 Type 1이다.

ex)

Plant가 1st order form에서

Characteristic equation :

따라서, 내가 원하는 natural frequency와 감쇠비가 있다면 그것에 맞게 고칠 수 있다.

Plant가 2nd order form에서
Characteristic equation :

여기서도 2개의 계수만 바꿀 수 있다.

Proportional-Integral-Derivative Control (PID)

$u(t)=k_pe(t)+k_I\int^te(\tau)d\tau+k_D\frac{de(t)}{dt}$
transfer function : $D_{cl}(s)=\frac{U(s)}{E(s)}=k_p+\frac{k_I}{s}+k_Ds=\frac{k_ps+k_I+k_Ds^2}{s}$

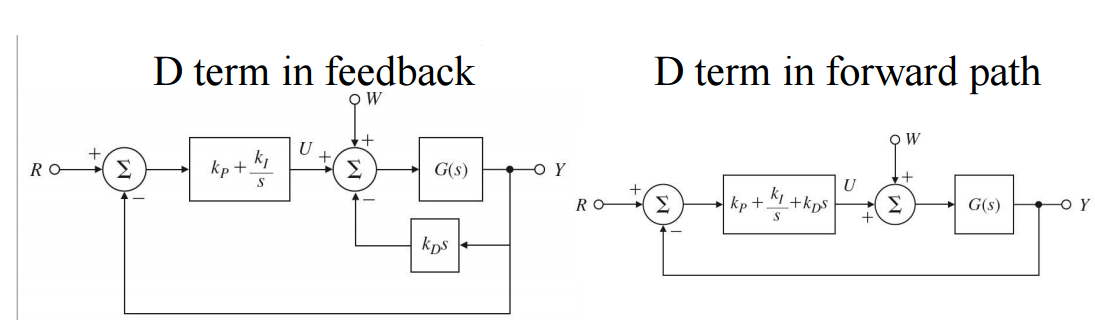
왼쪽 그림은 reference가 미분되기를 원치 않을 때 사용하면 된다.

Plant가 2nd order form일 때
Characteristic equation :

2nd order plant에서는 모든 계수를 바꿀수 있어 원하는 pole로 이동이 가능하다.

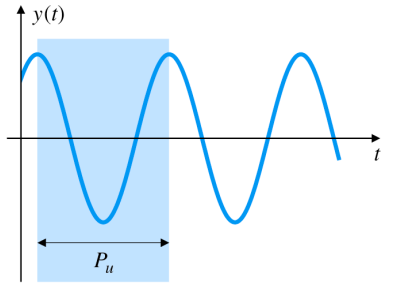
Ziegler-Nichols Tuning of the PID Controller

대부분의 경우 시스템의 모델을 알지 못한다. 이때, PID Control을 편히 사용하기 위해서 Ziegler-Nichols 방법을 사용해서 Gain을 튜닝한다.

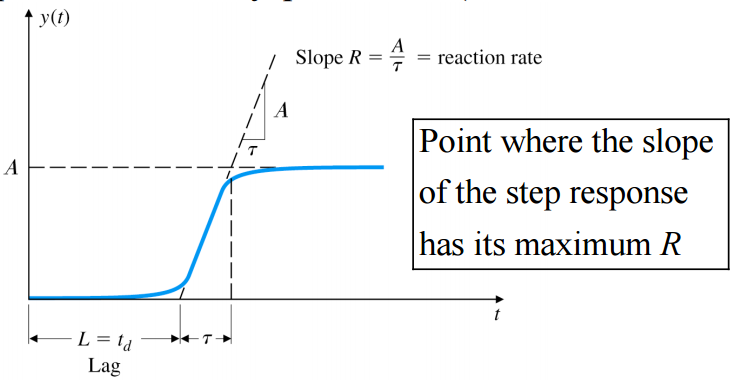
시스템이 1st-order system with time delay $t_d$ ($\frac{Y(s)}{U(s)}=\frac{Ae^{-st_d}}{\tau s+1}$)이라 가정 한다.

PID control : $D_c(s)=k_p[1+\frac{1}{T_Is}+T_Ds]$

• First method : L, R을 step response로 부터 구한다.(이때, 감쇠비는 0.21정도로 한다.)
  

• Second method : 이 방식은 P control을 추가하여 P gain이 작았을 때는 안정하다가 어느정도 커지기 시작하면 진동하여 불안정해지는 시스템에 적합하다.
  
  위 그림과 같이 $K_u$를 계속 키우다가 아래 그림과 같이 진동하였을 때를 찾는다.
  
  그때의 $K_u$를 통해 Controller의 gain을 얻는다.