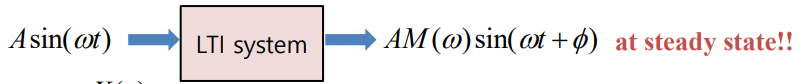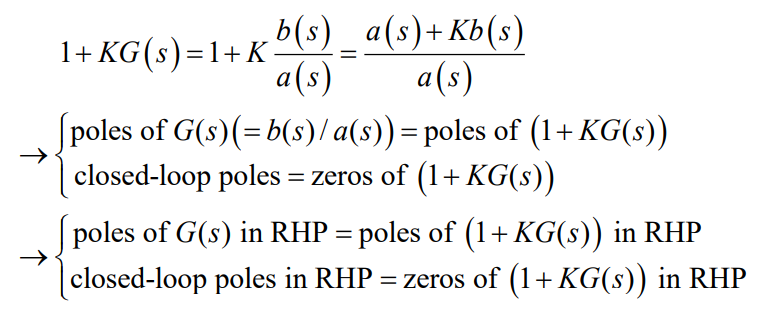이번 장에서는 시스템이 너무 복잡해서 모델을 모두 구하기 어려워 모델을 잘 모를때에 이 시스템에 주파수 응답 관점에서 시스템을 모델링 한다.
Frequency Response
Frequency response : sin파 입력에 대한 linear system의 응답G ( s ) = Y ( s ) U ( s ) G(s)=\frac{Y(s)}{U(s)} G ( s ) = U ( s ) Y ( s ) u ( t ) = A s i n ( ω 0 t ) 1 ( t ) → U ( s ) = A ω 0 s 2 + ω 0 2 u(t)=Asin(\omega_0t)1(t)\rightarrow U(s)=\frac{A\omega_0}{s^2+\omega_0^2} u ( t ) = A s i n ( ω 0 t ) 1 ( t ) → U ( s ) = s 2 + ω 0 2 A ω 0
( y ( 0 ) = 0 ) → Y ( s ) = G ( s ) A ω 0 s 2 + ω 0 2 (y(0)=0)\rightarrow Y(s)=G(s)\frac{A\omega_0}{s^2+\omega_0^2} ( y ( 0 ) = 0 ) → Y ( s ) = G ( s ) s 2 + ω 0 2 A ω 0 Output : compute y ( t ) y(t) y ( t ) G ( s ) G(s) G ( s )
Y ( s ) = α 1 s − p 1 + α 2 s − p 2 + ⋯ + α n s − p n + α 0 s + j ω 0 + α 0 ∗ s − j ω 0 → y ( t ) = α 1 e p 1 t + α 2 e p 2 t + ⋯ + α n e p n t + 2 ∣ α 0 ∣ sin ( ω 0 t + ϕ ) Y(s)=\frac{\alpha_1}{s-p_1}+\frac{\alpha_2}{s-p_2}+\cdots+\frac{\alpha_n}{s-p_n}+\frac{\alpha_0}{s+j\omega_0}+\frac{\alpha_0^*}{s-j\omega_0}\\ \rightarrow y(t)=\alpha_1e^{p_1t}+\alpha_2e^{p_2t}+\cdots+\alpha_ne^{p_nt}+2|\alpha_0|\sin(\omega_0t+\phi) Y ( s ) = s − p 1 α 1 + s − p 2 α 2 + ⋯ + s − p n α n + s + j ω 0 α 0 + s − j ω 0 α 0 ∗ → y ( t ) = α 1 e p 1 t + α 2 e p 2 t + ⋯ + α n e p n t + 2 ∣ α 0 ∣ sin ( ω 0 t + ϕ ) α 0 ∗ \alpha_0^* α 0 ∗
G ( j ω 0 ) = M ( ω 0 ) e j ϕ ( ω 0 ) ( M ( ω 0 ) = ∣ G ( j ω 0 ) ∣ = ∣ G ( s ) ∣ s = j ω 0 , ϕ ( ω 0 ) = tan − 1 I m [ G ( j ω 0 ) ] R e [ G ( j ω 0 ) ] = ∠ G ( j ω 0 ) ) G(j\omega_0)=M(\omega_0)e^{j\phi(\omega_0)}\\ (M(\omega_0)=|G(j\omega_0)|=|G(s)|_{s=j\omega_0},\;\phi(\omega_0)=\tan^{-1}\frac{Im[G(j\omega_0)]}{Re[G(j\omega_0)]}=\angle G(j\omega_0)) G ( j ω 0 ) = M ( ω 0 ) e j ϕ ( ω 0 ) ( M ( ω 0 ) = ∣ G ( j ω 0 ) ∣ = ∣ G ( s ) ∣ s = j ω 0 , ϕ ( ω 0 ) = tan − 1 R e [ G ( j ω 0 ) ] I m [ G ( j ω 0 ) ] = ∠ G ( j ω 0 ) ) 따라서,
α 0 ∗ = [ G ( s ) A ω 0 s 2 + ω 0 2 ( s − j ω 0 ) ] s = j ω 0 = G ( j ω 0 ) A ω 0 2 j ω 0 α 0 = ( α 0 ∗ ) ∗ = G ∗ ( j ω 0 ) A ω 0 − 2 j ω 0 = G ( − j ω 0 ) A ω 0 − 2 j ω 0 where, ϕ = ∠ [ G ( j ω 0 ) ] = tan − 1 ( R e ( α 0 ) I m ( α 0 ) ) α 0 s + j ω 0 + α 0 ∗ s − j ω 0 → A 2 j M e − j ϕ e − j ω 0 t − A 2 j M e j ϕ e j ω 0 t = A 2 j M ( − 2 j sin ( ω 0 t + ϕ ) ) = A M sin ( ω 0 t + ϕ ) \alpha_0^*=[G(s)\frac{A\omega_0}{s^2+\omega_0^2}(s-j\omega_0)]_{s=j\omega_0}=G(j\omega_0)\frac{A\omega_0}{2j\omega_0}\\ \alpha_0=(\alpha_0^*)^*=G^*(j\omega_0)\frac{A\omega_0}{-2j\omega_0}=G(-j\omega_0)\frac{A\omega_0}{-2j\omega_0}\\ \text{where, }\phi=\angle[G(j\omega_0)]=\tan^{-1}(\frac{Re(\alpha_0)}{Im(\alpha_0)})\\ \frac{\alpha_0}{s+j\omega_0}+\frac{\alpha_0^*}{s-j\omega_0}\rightarrow \frac{A}{2}jMe^{-j\phi}e^{-j\omega_0t}-\frac{A}{2}jMe^{j\phi}e^{j\omega_0t}\\ =\frac{A}{2}jM(-2j\sin(\omega_0t+\phi))\\ =AM\sin(\omega_0t+\phi) α 0 ∗ = [ G ( s ) s 2 + ω 0 2 A ω 0 ( s − j ω 0 ) ] s = j ω 0 = G ( j ω 0 ) 2 j ω 0 A ω 0 α 0 = ( α 0 ∗ ) ∗ = G ∗ ( j ω 0 ) − 2 j ω 0 A ω 0 = G ( − j ω 0 ) − 2 j ω 0 A ω 0 where, ϕ = ∠ [ G ( j ω 0 ) ] = tan − 1 ( I m ( α 0 ) R e ( α 0 ) ) s + j ω 0 α 0 + s − j ω 0 α 0 ∗ → 2 A j M e − j ϕ e − j ω 0 t − 2 A j M e j ϕ e j ω 0 t = 2 A j M ( − 2 j sin ( ω 0 t + ϕ ) ) = A M sin ( ω 0 t + ϕ ) 위 식을 통해 Magnitude는 전달함수에 j ω 0 j\omega_0 j ω 0 j ω 0 j\omega_0 j ω 0
주파수 응답은 실험적으로 구할 수 있다. 가장 쉽게 구할 수 있는 방법은 여러 주파수에 대해서 sin파를 넣어보는 것이다. 그에 따른 응답을 통해 magnitude와 phase shift를 구하여 bode plot을 통해 frequency response를 구한다.
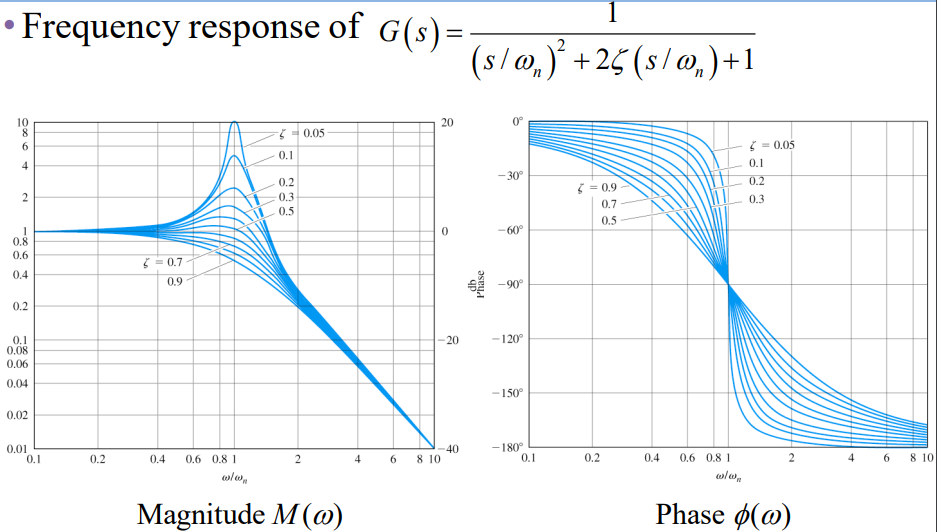
시스템의 dynamic response는 전달함수의 magnitude와 phase shift를 알면 결정할 수 있다. 어떤 입력이 periodic input이라고 한다면 그것은 푸리에 시리즈로 전개할 수 있다.ω n \omega_n ω n s = j ω s=j\omega s = j ω
1 ( j ω ω n ) 2 + 2 ζ j ω ω n + 1 = ∣ 1 [ 1 − ( ω ω n ) 2 ] 2 + 4 ζ 2 ( ω ω n ) 2 ∣ ∠ tan − 1 2 ζ ω ω n 1 − ( ω ω n ) 2 \frac{1}{(\frac{j\omega}{\omega_n})^2+2\zeta\frac{j\omega}{\omega_n}+1} =\left|\frac{1}{\sqrt{[1-(\frac{\omega}{\omega_n})^2}]^2+4\zeta^2(\frac{\omega}{\omega_n})^2}\right|\angle{\tan^{-1}\frac{2\zeta\frac{\omega}{\omega_n}}{1-(\frac{\omega}{\omega_n})^2}} ( ω n j ω ) 2 + 2 ζ ω n j ω + 1 1 = ∣ ∣ ∣ ∣ ∣ ∣ ∣ [ 1 − ( ω n ω ) 2 ] 2 + 4 ζ 2 ( ω n ω ) 2 1 ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∠ tan − 1 1 − ( ω n ω ) 2 2 ζ ω n ω ω ≪ ω n \omega\ll\omega_n ω ≪ ω n ω \omega ω ω \omega ω ω ω n = 1 \frac{\omega}{\omega_n}=1 ω n ω = 1 1 2 ζ \frac{1}{2\zeta} 2 ζ 1 ζ \zeta ζ
Bandwidth and resonance peak
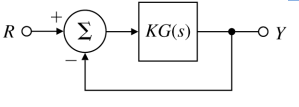
우리가 궁극적으로 원하는 것은 밑의 그림과 같은 closed-loop 시스템에 제어를 통해 원하는 응답을 얻어내는 것이다.
Y ( s ) R ( s ) = T ( s ) = K G ( s ) 1 + K G ( s ) Typically, { ∣ T ∣ ≅ 1 for low frequencies ∣ T ∣ < 1 for high frequencies \frac{Y(s)}{R(s)}=T(s)=\frac{KG(s)}{1+KG(s)}\\ \text{Typically, }\begin{cases}|T|\cong1\text{ for low frequencies}\\ |T|<1\text{ for high frequencies}\end{cases} R ( s ) Y ( s ) = T ( s ) = 1 + K G ( s ) K G ( s ) Typically, { ∣ T ∣ ≅ 1 for low frequencies ∣ T ∣ < 1 for high frequencies
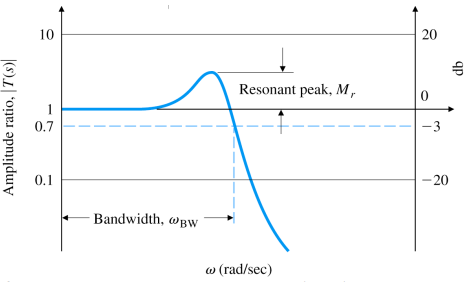
Resonance peak M r M_r M r ω B W \omega_{BW} ω B W 1 / 2 1/\sqrt{2} 1 / 2
Second order system with closed-loop transfer function
T ( s ) = 1 ( s / ω n ) 2 + 2 ζ ( s / ω n ) + 1 T(s)=\frac{1}{(s/\omega_n)^2+2\zeta(s/\omega_n)+1} T ( s ) = ( s / ω n ) 2 + 2 ζ ( s / ω n ) + 1 1 ζ = 0.7 \zeta = 0.7 ζ = 0 . 7 ω n = ω B W \omega_n=\omega_{BW} ω n = ω B W ω B W ≤ 2 ω n \omega_{BW}\leq2\omega_n ω B W ≤ 2 ω n
따라서, bandwidth를 통해서 natural frequency와 damping ratio를 결정 지을 수 있으므로 frequency response 영역에서는 bandwidth를 아는 것이 중요하다.
Bode Plot Techniques
Bode plot은 주파수 응답을 그래프로 나타낸 것이다.
Decibel(d b db d b
∣ G ∣ d b = 10 log 10 P 2 P 1 ∣ G ∣ d b = 20 log 10 V 2 V 1 ( P 1 ∝ V 1 2 , P 2 ∝ V 2 2 ) |G|_{db}=10\log_{10}\frac{P_2}{P_1}\\ |G|_{db}=20\log_{10}\frac{V_2}{V_1}\quad(P_1 \propto V_1^2,\;P_2 \propto V_2^2) ∣ G ∣ d b = 1 0 log 1 0 P 1 P 2 ∣ G ∣ d b = 2 0 log 1 0 V 1 V 2 ( P 1 ∝ V 1 2 , P 2 ∝ V 2 2 ) Bode plot의 장점
제어기 설계에 사용 가능하다.
실험적으로 구할 수 있다.
시리즈로 연결된 bode plot은 더하면 된다.
log scale은 넓은 주파수 영역에서 생각하기 위해 사용된다.
Plotting Bode plots
transfer function
K G ( s ) = K ( s − z 1 ) ( s − z 2 ) ⋯ ( s − p 1 ) ( s − p 2 ) ⋯ ⟹ K G ( j ω ) = K 0 ( j ω τ 1 + 1 ) ( j ω τ 2 + 1 ) ⋯ ( j ω τ a + 1 ) ( j ω τ b + 1 ) ⋯ ∠ ( K G ( j ω ) ) = ∠ ( j ω τ 1 + 1 ) + ∠ ( j ω τ 2 + 1 ) + ⋯ − ∠ ( j ω τ a + 1 ) − ∠ ( j ω τ b + 1 ) − ⋯ ∣ K G ( j ω ) ∣ d b = ∣ ( j ω τ 1 + 1 ) ∣ d b + ∣ ( j ω τ 2 + 1 ) ∣ d b + ⋯ − ∣ ( j ω τ a + 1 ) ∣ d b − ∣ ( j ω τ b + 1 ) ∣ d b − ⋯ KG(s)=K\frac{(s-z_1)(s-z_2)\cdots}{(s-p_1)(s-p_2)\cdots}\Longrightarrow KG(j\omega)=K_0\frac{(j\omega\tau_1+1)(j\omega\tau_2+1)\cdots}{(j\omega\tau_a+1)(j\omega\tau_b+1)\cdots}\\ \angle(KG(j\omega))=\angle(j\omega\tau_1+1)+\angle(j\omega\tau_2+1)+\cdots-\angle(j\omega\tau_a+1)-\angle(j\omega\tau_b+1)-\cdots\\ |KG(j\omega)|_{db}=|(j\omega\tau_1+1)|_{db}+|(j\omega\tau_2+1)|_{db}+\cdots-|(j\omega\tau_a+1)|_{db}-|(j\omega\tau_b+1)|_{db}-\cdots K G ( s ) = K ( s − p 1 ) ( s − p 2 ) ⋯ ( s − z 1 ) ( s − z 2 ) ⋯ ⟹ K G ( j ω ) = K 0 ( j ω τ a + 1 ) ( j ω τ b + 1 ) ⋯ ( j ω τ 1 + 1 ) ( j ω τ 2 + 1 ) ⋯ ∠ ( K G ( j ω ) ) = ∠ ( j ω τ 1 + 1 ) + ∠ ( j ω τ 2 + 1 ) + ⋯ − ∠ ( j ω τ a + 1 ) − ∠ ( j ω τ b + 1 ) − ⋯ ∣ K G ( j ω ) ∣ d b = ∣ ( j ω τ 1 + 1 ) ∣ d b + ∣ ( j ω τ 2 + 1 ) ∣ d b + ⋯ − ∣ ( j ω τ a + 1 ) ∣ d b − ∣ ( j ω τ b + 1 ) ∣ d b − ⋯ Elements of Bode plots (three classes)
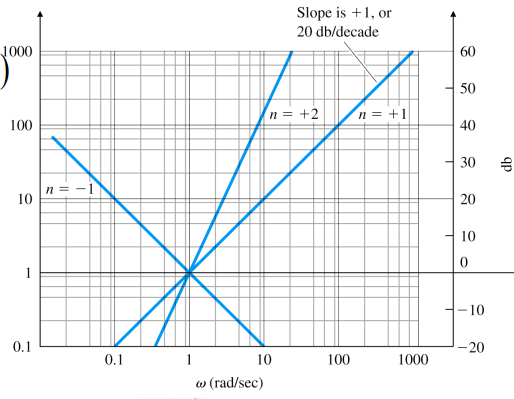
K 0 ( j ω ) n K_0(j\omega)^n K 0 ( j ω ) n
log ∣ K 0 ( j ω ) n ∣ = log ∣ K 0 ∣ + n log ∣ j ω ∣ ( Y = K + n Ω , K = l o g ∣ K 0 ∣ , Ω = log ω ) → 20 log ∣ K 0 ( j ω ) n ∣ = 20 log ∣ K 0 ∣ + 20 n log ω ∠ ( j ω ) n = n × 90 ° \log\left|K_0(j\omega)^n\right|=\log\left|K_0\right|+n\log\left|j\omega\right|\\ \left(Y=K+n\Omega,\; K=log\left|K_0\right|,\;\Omega=\log\omega\right)\\ \rightarrow 20\log\left|K_0(j\omega)^n\right|=20\log\left|K_0\right|+20n\log\omega\\ \angle(j\omega)^n=n\times90\degree log ∣ K 0 ( j ω ) n ∣ = log ∣ K 0 ∣ + n log ∣ j ω ∣ ( Y = K + n Ω , K = l o g ∣ K 0 ∣ , Ω = log ω ) → 2 0 log ∣ K 0 ( j ω ) n ∣ = 2 0 log ∣ K 0 ∣ + 2 0 n log ω ∠ ( j ω ) n = n × 9 0 ° log ω \log\omega log ω
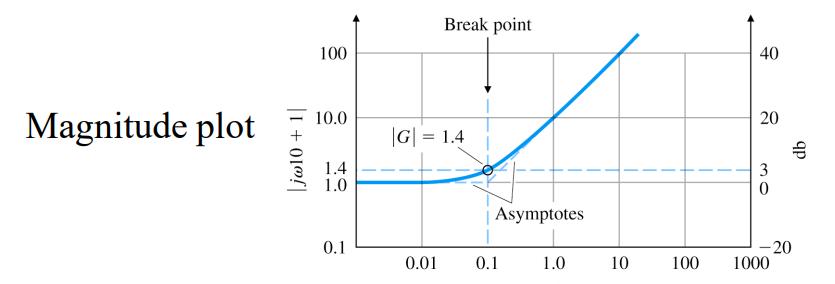
( j ω τ + 1 ) ± 1 (j\omega\tau+1)^{\pm 1} ( j ω τ + 1 ) ± 1
{ ω τ ≪ 1 ⇒ j ω τ + 1 ≅ 1 ⇒ log ∣ j ω τ + 1 ∣ ≅ 0 ω τ ≫ 1 ⇒ j ω τ + 1 ≅ j ω τ ⇒ log ∣ j ω τ + 1 ∣ ≅ log ∣ j ω τ ∣ = log ∣ τ ∣ + log ∣ j ω ∣ ( ω = 1 / τ = break point ← log ∣ τ ∣ + log ∣ j ( 1 / τ ) ∣ = 0 ) \begin{cases} \omega\tau\ll1\Rightarrow j\omega\tau+1\cong1\Rightarrow\log\left|j\omega\tau+1\right|\cong0\\ \omega\tau\gg1\Rightarrow j\omega\tau+1\cong j\omega\tau\Rightarrow\log\left|j\omega\tau+1\right|\cong\log\left|j\omega\tau\right|=\log\left|\tau\right|+\log\left|j\omega\right| \end{cases}\\ (\omega=1/\tau=\text{break point}\leftarrow\log\left|\tau\right|+\log\left|j(1/\tau)\right|=0) { ω τ ≪ 1 ⇒ j ω τ + 1 ≅ 1 ⇒ log ∣ j ω τ + 1 ∣ ≅ 0 ω τ ≫ 1 ⇒ j ω τ + 1 ≅ j ω τ ⇒ log ∣ j ω τ + 1 ∣ ≅ log ∣ j ω τ ∣ = log ∣ τ ∣ + log ∣ j ω ∣ ( ω = 1 / τ = break point ← log ∣ τ ∣ + log ∣ j ( 1 / τ ) ∣ = 0 ) 여기서는 bode plot을 근사해서 그린다.
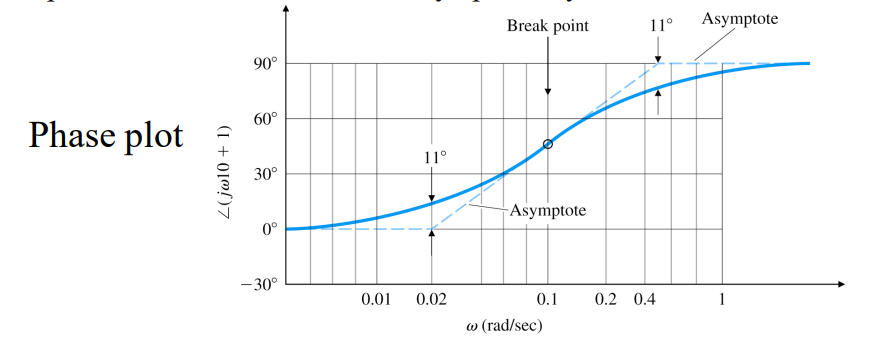
{ ω τ ≪ 1 ⇒ ∠ ( j ω τ + 1 ) ≅ ∠ 1 = 0 ° ω τ ≫ 1 ⇒ ∠ ( j ω τ + 1 ) ≅ ∠ j ω τ = 90 ° ω τ ≅ 1 ⇒ ∠ ( j ω τ + 1 ) ≅ 45 ° ( ω = 1 / τ = break point ) \begin{cases} \omega\tau\ll1\Rightarrow\angle(j\omega\tau+1)\cong\angle1=0\degree\\ \omega\tau\gg1\Rightarrow\angle(j\omega\tau+1)\cong\angle j\omega\tau=90\degree\\ \omega\tau\cong1\Rightarrow\angle(j\omega\tau+1)\cong45\degree\;(\omega=1/\tau=\text{break point}) \end{cases} ⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ ω τ ≪ 1 ⇒ ∠ ( j ω τ + 1 ) ≅ ∠ 1 = 0 ° ω τ ≫ 1 ⇒ ∠ ( j ω τ + 1 ) ≅ ∠ j ω τ = 9 0 ° ω τ ≅ 1 ⇒ ∠ ( j ω τ + 1 ) ≅ 4 5 ° ( ω = 1 / τ = break point )
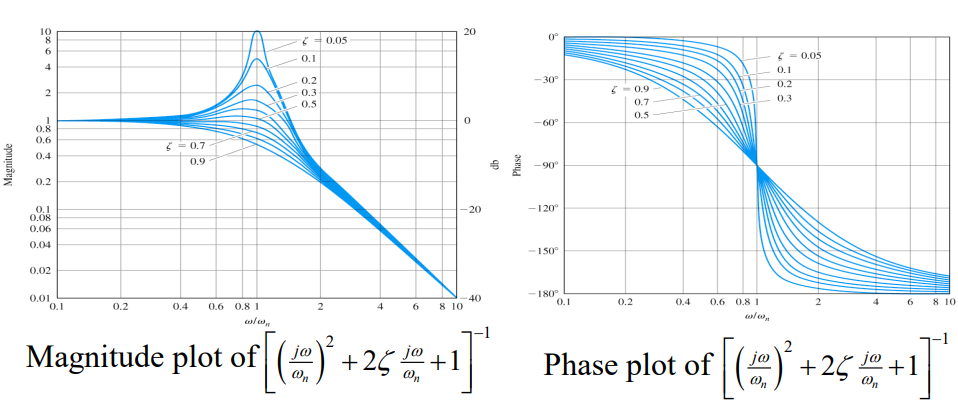
[ ( j ω ω n ) 2 + 2 ζ j ω ω n + 1 ] ± 1 \left[(\frac{j\omega}{\omega_n})^2+2\zeta\frac{j\omega}{\omega_n}+1\right]^{\pm1} [ ( ω n j ω ) 2 + 2 ζ ω n j ω + 1 ] ± 1
{ ω ≪ ω n ⇒ G ( j ω ) ≅ 1 ⇒ log ∣ G ( j ω ) ∣ ≅ 0 ω ≫ ω n ⇒ G ( j ω ) ≅ ( j ω / ω n ) ± 2 ⇒ log ∣ G ( j ω ) ∣ ≅ ± 2 log ∣ 1 / ω n ∣ ± log ∣ ( j ω ) ∣ \begin{cases} \omega\ll\omega_n\Rightarrow G(j\omega)\cong1\Rightarrow\log|G(j\omega)|\cong0\\ \omega\gg\omega_n\Rightarrow G(j\omega)\cong(j\omega/\omega_n)^{\pm2}\Rightarrow\log|G(j\omega)|\cong\pm2\log|1/\omega_n|\pm\log|(j\omega)| \end{cases} { ω ≪ ω n ⇒ G ( j ω ) ≅ 1 ⇒ log ∣ G ( j ω ) ∣ ≅ 0 ω ≫ ω n ⇒ G ( j ω ) ≅ ( j ω / ω n ) ± 2 ⇒ log ∣ G ( j ω ) ∣ ≅ ± 2 log ∣ 1 / ω n ∣ ± log ∣ ( j ω ) ∣ Break point : ω = ω n \omega = \omega_n ω = ω n
Summary of Bode Plot Rules
trnasfer function을 bode form으로 바꾼다.
제일 낮은 frequency에서는 그래프의 모양이 K 0 ( j ω ) n K_0(j\omega)^n K 0 ( j ω ) n ω = 1 \omega=1 ω = 1 K 0 K_0 K 0
모든 break point들을 찾아 break point지점에서 그래프가 상승하는지 하강하는지를 확인한다.
1차항에 경우에는 그래프의 모양을 ± 3 d b \pm3db ± 3 d b ω = ω n \omega=\omega_n ω = ω n ∣ G ( j ω ) ∣ = 1 2 ζ |G(j\omega)|=\frac{1}{2\zeta} ∣ G ( j ω ) ∣ = 2 ζ 1 ∣ G ( j ω ) = 2 ζ ∣ |G(j\omega)=2\zeta| ∣ G ( j ω ) = 2 ζ ∣
Phase 그래프도 낮은 주파수에서는 ϕ = n × 90 ° \phi = n\times90\degree ϕ = n × 9 0 °
각 break point를 지나면서 1차항인 경우에는 ± 90 ° \pm90\degree ± 9 0 ° ± \1 80 ° \pm\180\degree ± \1 8 0 °
Minimum phase versus nonminimum phase
Minimum phase system : 시스템의 zero가 모두 LHP에 있는 경우
Nonminimum phase system : 시스템의 몇몇 zero가 RHP에 있는 경우
ex)
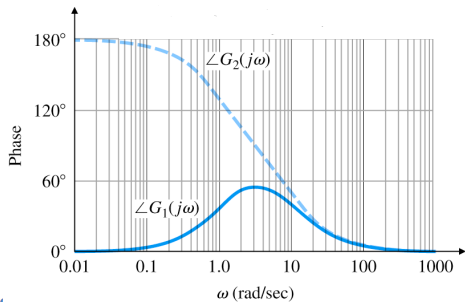
minimum-phase : G 1 ( s ) = 10 s + 1 s + 10 G_1(s)=10\cfrac{s+1}{s+10} G 1 ( s ) = 1 0 s + 1 0 s + 1 G 2 ( s ) = 10 s − 1 s + 10 G_2(s)=10\cfrac{s-1}{s+10} G 2 ( s ) = 1 0 s + 1 0 s − 1
∣ G 1 ( j ω ) ∣ = ∣ G 2 ( j ω ) ∣ |G_1(j\omega)|=|G_2(j\omega)| ∣ G 1 ( j ω ) ∣ = ∣ G 2 ( j ω ) ∣
Steady-state errors from Bode plots
open-loop low frequency 근사는 다음과 같다.
K G ( j ω ) = K 0 ( j ω ) n Π i ( j ω τ i + 1 ) Π a ( j ω τ a + 1 ) ≅ K 0 ( j ω ) n KG(j\omega)=K_0(j\omega)^n\cfrac{\Pi_i(j\omega\tau_i+1)}{\Pi_a(j\omega\tau_a+1)}\cong K_0(j\omega)^n K G ( j ω ) = K 0 ( j ω ) n Π a ( j ω τ a + 1 ) Π i ( j ω τ i + 1 ) ≅ K 0 ( j ω ) n 이때, n = 0 n=0 n = 0 K 0 K_0 K 0
e s s = 1 1 + K p = 1 1 + K 0 ( K p = lim s → 0 K G ( s ) ) e_{ss}=\frac{1}{1+K_p}=\frac{1}{1+K_0}\;\left(K_p=\lim_{s\rightarrow0}KG(s)\right) e s s = 1 + K p 1 = 1 + K 0 1 ( K p = s → 0 lim K G ( s ) ) n = − 1 n=-1 n = − 1
K v = K 0 ( K v = lim s → 0 s K G ( s ) ) ⇒ e s s = 1 K v = 1 K 0 K_v=K_0\;\left(K_v=\lim_{s\rightarrow0}sKG(s)\right)\Rightarrow e_{ss}=\frac{1}{K_v}=\frac{1}{K_0} K v = K 0 ( K v = s → 0 lim s K G ( s ) ) ⇒ e s s = K v 1 = K 0 1 Neutral Stability
Frequency response를 가지고 closed-loop system의 안정성을 판별할 수 있는가?
ex)
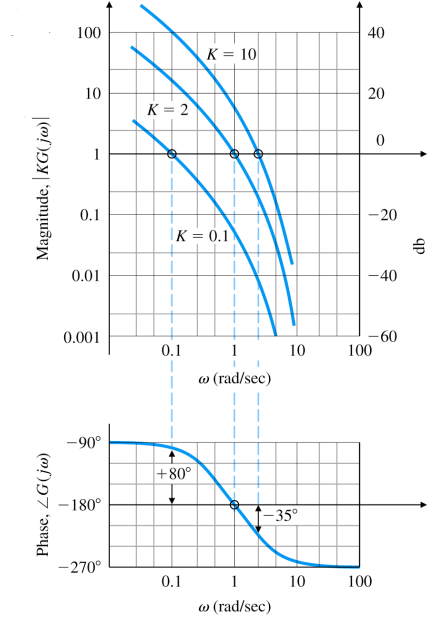
1 + K G ( s ) = 0 → ∣ K G ( s ) ∣ = 1 , ∠ G ( s ) = 180 ° ( G ( s ) = − 1 / K ) Neutral stability point : K = 2 , s = j 1 = j ω 0 1+KG(s)=0\rightarrow|KG(s)|=1,\quad\angle G(s)=180\degree\;(G(s)=-1/K)\\ \text{Neutral stability point : }K=2,\;s=j1=j\omega_0 1 + K G ( s ) = 0 → ∣ K G ( s ) ∣ = 1 , ∠ G ( s ) = 1 8 0 ° ( G ( s ) = − 1 / K ) Neutral stability point : K = 2 , s = j 1 = j ω 0 Closed-loop의 bode plot을 그리게 되면 다음과 같다.
K = 2 neutrally stable K=2\;\text{ neutrally stable} K = 2 neutrally stable
∣ K G ( j ω ) ∣ = 1 , at ω where ∠ G ( j ω ) = − 180 ° |KG(j\omega)|=1,\text{ at }\omega\text{ where }\angle G(j\omega)=-180\degree ∣ K G ( j ω ) ∣ = 1 , at ω where ∠ G ( j ω ) = − 1 8 0 °
∣ K G ( j ω ) ∣ < 1 , at ω where ∠ G ( j ω ) = − 180 ° |KG(j\omega)|<1,\text{ at }\omega\text{ where }\angle G(j\omega)=-180\degree ∣ K G ( j ω ) ∣ < 1 , at ω where ∠ G ( j ω ) = − 1 8 0 °
⟺ K < 2 → stable \iff K < 2\rightarrow \text{stable} ⟺ K < 2 → stable
∣ K G ( j ω ) ∣ > 1 , at ω where ∠ G ( j ω ) = − 180 ° |KG(j\omega)|>1,\text{ at }\omega\text{ where }\angle G(j\omega)=-180\degree ∣ K G ( j ω ) ∣ > 1 , at ω where ∠ G ( j ω ) = − 1 8 0 °
⟺ K > 2 → unstable \iff K > 2\rightarrow \text{unstable} ⟺ K > 2 → unstable
따라서, gain이 커질수록 시스템은 unstable 해진다.
보통 시스템은 gain이 커질수록 시스템이 덜 안정해진다. 하지만 모든 시스템에 적용되는 것은 아니다. 이를 판별하기 위해서 Nyquist stability criterion을 사용한다.
Nyquist stability criterion
Nyquist stability criterion은 주파수 응답을 통해 closed-loop system의 안정도를 판별하는 완벽한 방법이다. Bode plot만 가지고는 안정도를 판별할 수 없다. Nyquist stability criterion은 argument principle을 기본으로 하고있다.
Nyquist plot : K G ( s ) KG(s) K G ( s )
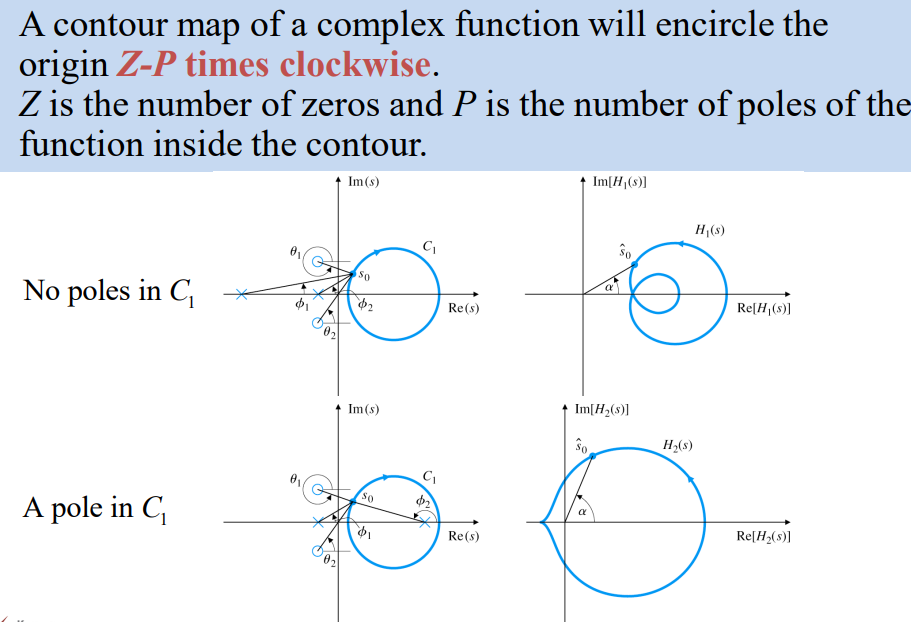
Argument principle
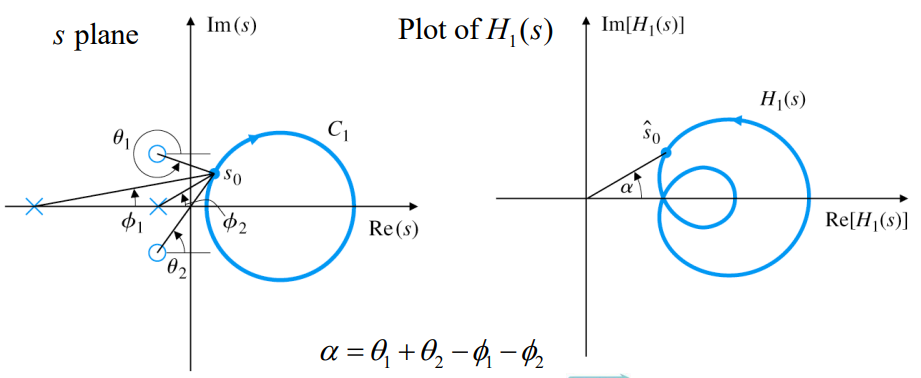
Contour evaluation : 주어진 전달함수 H ( s ) H(s) H ( s )
이때, contour evaluation안에 pole이나 zero의 갯수에 따라 전달함수의 plot의 방향이 달라진다.
Z > P → ( Z − P ) clockwise encirclements around the origin Z>P\rightarrow(Z-P) \text{ clockwise encirclements around the origin} Z > P → ( Z − P ) clockwise encirclements around the origin Z < P → ( P − Z ) counterclockwise encirclements around the origin Z<P\rightarrow(P-Z) \text{ counterclockwise encirclements around the origin} Z < P → ( P − Z ) counterclockwise encirclements around the origin
즉, Z − P Z-P Z − P
이 관점은 Nyquist stability criterion에서도 똑같이 적용된다.H ( s ) → 1 + K G ( s ) H(s)\rightarrow 1+KG(s) H ( s ) → 1 + K G ( s ) 1 + K G ( s ) 1+KG(s) 1 + K G ( s ) 1 + K G ( s ) 1+KG(s) 1 + K G ( s ) K G ( s ) KG(s) K G ( s )
contour가 RHP이므로 contour안에 zero,pole 갯수는 RHP에 zero, pole의 갯수와 같다.
정리를 해보면 다음과 같다.
따라서, closed-loop system의 안정성은 RHP방면에 open-loop system의 pole이 몇개 있는지와 Nyquist plot으로 결정할 수 있다.
Procefure of plotting the Nyquist plot
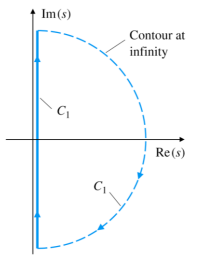
Contour C 1 C_1 C 1 K G ( s ) KG(s) K G ( s ) K G ( s ) KG(s) K G ( s ) − j ∞ ≤ s ≤ + j ∞ -j\infty\leq s\leq+j\infty − j ∞ ≤ s ≤ + j ∞ K G ( s ) KG(s) K G ( s )
− 1 -1 − 1 N N N
open-loop system의 pole이 RHP에 몇 개(P P P
Z = N + P Z=N+P Z = N + P
Z = 0 → The closed loop system is stable Z > 0 → The closed loop system is unstable Z = 0 \rightarrow \text{The closed loop system is stable}\\ Z > 0 \rightarrow \text{The closed loop system is unstable} Z = 0 → The closed loop system is stable Z > 0 → The closed loop system is unstable
ex)
Nyquist plot for a third order system
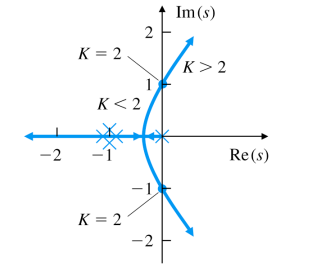
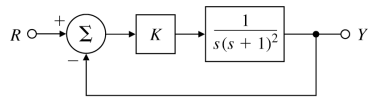
G ( s ) = 1 s ( s + 1 ) 2 G(s)=\frac{1}{s(s+1)^2} G ( s ) = s ( s + 1 ) 2 1
Pole이 원점에 있어서 contour C 1 C_1 C 1
우회하는 부분의 contour를 살펴보자면 s = r e j θ s=re^{j\theta} s = r e j θ r ≪ 1 r\ll1 r ≪ 1 θ \theta θ − 90 ° -90\degree − 9 0 ° 90 ° 90\degree 9 0 ° θ = − 90 ° → 0 ° → 90 ° \theta=-90\degree\rightarrow0\degree\rightarrow90\degree θ = − 9 0 ° → 0 ° → 9 0 °
⇒ G ( s ) = 1 s ( s + 1 ) 2 ≅ 1 s = 1 r e j θ = 1 r e j ( − θ ) 1 r ≫ 1 , − 90 ° ≤ − θ ≤ 90 ° ( − θ = 90 ° → 0 ° → − 90 ° ) \Rightarrow G(s)=\frac{1}{s(s+1)^2}\cong\frac{1}{s}=\frac{1}{re^{j\theta}}=\frac{1}{r}e^{j(-\theta)}\\ \frac{1}{r}\gg1,\;-90\degree\leq-\theta\leq90\degree\;(-\theta=90\degree\rightarrow0\degree\rightarrow-90\degree) ⇒ G ( s ) = s ( s + 1 ) 2 1 ≅ s 1 = r e j θ 1 = r 1 e j ( − θ ) r 1 ≫ 1 , − 9 0 ° ≤ − θ ≤ 9 0 ° ( − θ = 9 0 ° → 0 ° → − 9 0 ° ) 이를 바탕으로 Nyquist plot을 그려보면 다음과 같다.G ( j ω ) G(j\omega) G ( j ω ) ω = 1 \omega=1 ω = 1 ∣ G ( j 1 ) ∣ = 0.5 |G(j1)|=0.5 ∣ G ( j 1 ) ∣ = 0 . 5
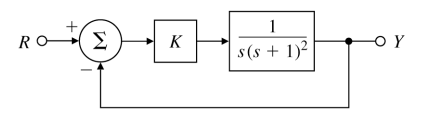
1 + K G ( s ) = 0 , G ( s ) = − 1 / K − 0.5 < − 1 / K < 0 → N = 2 , → Z = N + P = 2 + 0 = 2 → u n s t a b l e − 1 / K < − 0.5 → N = 0 , → Z = N + P = 0 + 0 = 0 → s t a b l e 1+KG(s)=0,\;G(s)=-1/K\\ -0.5<-1/K<0\rightarrow N=2,\\ \rightarrow Z=N+P=2+0=2\rightarrow unstable\\ -1/K<-0.5\rightarrow N=0,\\ \rightarrow Z=N+P=0+0=0\rightarrow stable 1 + K G ( s ) = 0 , G ( s ) = − 1 / K − 0 . 5 < − 1 / K < 0 → N = 2 , → Z = N + P = 2 + 0 = 2 → u n s t a b l e − 1 / K < − 0 . 5 → N = 0 , → Z = N + P = 0 + 0 = 0 → s t a b l e 원점에 pole이 여러개 있다면 어떻게 될까?
G ( s ) = 1 s k ( s + 1 ) 2 , k ≥ 1 s = r e j θ , r ≪ 1 , − 90 ° ≤ θ ≤ 90 ° ( θ = − 90 ° → 0 ° → 90 ° ) ⇒ G ( s ) = 1 s k ( s + 1 ) 2 ≅ 1 s k = 1 r k e j k θ = 1 r k e j ( − k θ ) , 1 r k ≫ 1. − k 90 ° ≤ − k θ ≤ k 90 ° ( − k θ = k 90 ° → 0 ° → − k 90 ° ) G(s)=\frac{1}{s^k(s+1)^2},\;k\geq1\\ s=re^{j\theta},\;r\ll1,\;-90\degree\leq\theta\leq90\degree\;(\theta=-90\degree\rightarrow0\degree\rightarrow90\degree)\\ \Rightarrow G(s)=\frac{1}{s^k(s+1)^2}\cong\frac{1}{s^k}=\frac{1}{r^ke^{jk\theta}}=\frac{1}{r^k}e^{j(-k\theta)},\\ \frac{1}{r^k}\gg1.\;-k90\degree\leq-k\theta\leq k90\degree\;(-k\theta=k90\degree\rightarrow0\degree\rightarrow-k90\degree) G ( s ) = s k ( s + 1 ) 2 1 , k ≥ 1 s = r e j θ , r ≪ 1 , − 9 0 ° ≤ θ ≤ 9 0 ° ( θ = − 9 0 ° → 0 ° → 9 0 ° ) ⇒ G ( s ) = s k ( s + 1 ) 2 1 ≅ s k 1 = r k e j k θ 1 = r k 1 e j ( − k θ ) , r k 1 ≫ 1 . − k 9 0 ° ≤ − k θ ≤ k 9 0 ° ( − k θ = k 9 0 ° → 0 ° → − k 9 0 ° ) Nyquist plot을 그려보면 k / 2 k/2 k / 2
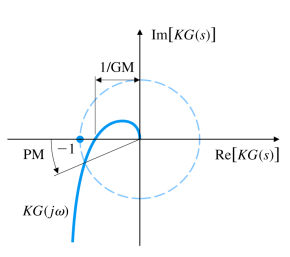
Stability Margins
지금까지는 안정한지 안정하지 않은지를 판별했다면은 이번에는 얼마나 안정한지를 판별한다.
Gain margin(GM) : 초기 stable했을 때의 gain에 비해서 gain을 계속 키웠을 때 unstable해지는 비율이다.
Phase margin(PM) : ∣ K G ( j ω ) ∣ = 1 |KG(j\omega)|=1 ∣ K G ( j ω ) ∣ = 1 G ( j ω ) G(j\omega) G ( j ω )
이는 Neutral stability condition( ∣ K G ( j ω ) ∣ = 1 , ∠ K G ( j ω ) = − 180 ° |KG(j\omega)|=1,\;\angle KG(j\omega)=-180\degree ∣ K G ( j ω ) ∣ = 1 , ∠ K G ( j ω ) = − 1 8 0 °
Crossover frequency ( ω c \omega_c ω c
Find PM for different values of K
∣ K G ( j ω ) ∣ = 1 |KG(j\omega)|=1 ∣ K G ( j ω ) ∣ = 1 ω c \omega_c ω c
이에 상응하는 PM을 찾는다.
Find K for a desired PM
주어진 PM만큼 phase가 떨어진 곳의 frequency를 찾는다.
이때에 맞는 K K K
Relation between PM and damping ratio
open loop 2nd-order system : G ( s ) = ω n 2 s ( s + 2 ζ ω n ) G(s)=\cfrac{\omega^2_n}{s(s+2\zeta\omega_n)} G ( s ) = s ( s + 2 ζ ω n ) ω n 2 T ( s ) = ω n 2 s 2 + 2 ζ ω n s + ω n 2 T(s)=\cfrac{\omega^2_n}{s^2+2\zeta\omega_ns+\omega^2_n} T ( s ) = s 2 + 2 ζ ω n s + ω n 2 ω n 2
먼저 crossover frequency를 찾는다. ∣ G ( j ω c ) ∣ = 1 |G(j\omega_c)|=1 ∣ G ( j ω c ) ∣ = 1 − 180 ° -180\degree − 1 8 0 ° ∠ G ( j ω c ) + 180 ° \angle G(j\omega_c)+180\degree ∠ G ( j ω c ) + 1 8 0 °
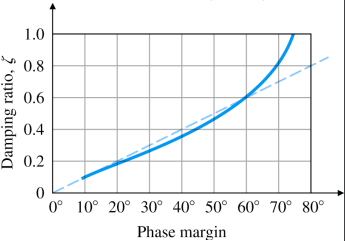
⇒ PM = tan − 1 [ 2 ζ 1 + 4 ζ 4 − 2 ζ 2 ] \Rightarrow \text{PM}=\tan^{-1}\left[\cfrac{2\zeta}{\sqrt{\sqrt{1+4\zeta^4}-2\zeta^2}}\right] ⇒ PM = tan − 1 ⎣ ⎢ ⎡ 1 + 4 ζ 4 − 2 ζ 2 2 ζ ⎦ ⎥ ⎤ PM = 70 ° \text{PM}=70\degree PM = 7 0 ° ζ ≅ PM 100 \zeta\cong\cfrac{\text{PM}}{100} ζ ≅ 1 0 0 PM
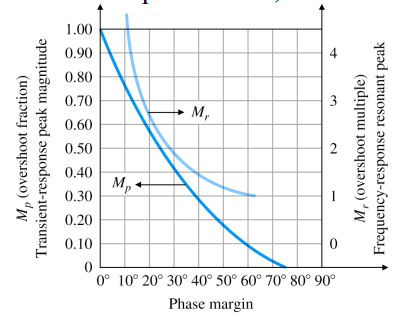
Resonant peak와 PM의 관계는 다음과 같다.Resonant peak \text{Resonant peak} Resonant peak 1 2 ζ \cfrac{1}{2\zeta} 2 ζ 1
페이즈 마진은 감쇠비에 영향이 많으므로 감쇠비와 같다라고 보면 된다.
Crossover frequency는 closd-loop의 bandwidth와 관련있다.
1st/2nd order system은 phase가 180 ° 180\degree 1 8 0 ° ∞ \infty ∞
2차 이상 고차 system은 ∣ K G ( j ω ) ∣ = 1 |KG(j\omega)|=1 ∣ K G ( j ω ) ∣ = 1 ∠ K G ( j ω ) = − 180 ° \angle KG(j\omega)=-180\degree ∠ K G ( j ω ) = − 1 8 0 °
Conditionally stable system : gain을 키웠을 때 system이 stable 해지는 것을 의미한다.
Bode's Gain-Phase Relationship
stable한 minimum phase system에서 ∠ G ( j ω ) \angle G(j\omega) ∠ G ( j ω ) ∣ G ( j ω ) ∣ |G(j\omega)| ∣ G ( j ω ) ∣ ∣ G ( j ω ) ∣ |G(j\omega)| ∣ G ( j ω ) ∣ 20 n db/decade 20n\text{ db/decade} 2 0 n db/decade ∠ G ( j ω ) ≅ n × 90 ° \angle G(j\omega)\cong n\times90\degree ∠ G ( j ω ) ≅ n × 9 0 °
시스템이 안정적이려면 PM > 0 \text{PM} > 0 PM > 0 ∠ G ( j ω ) > − 180 ° \angle G(j\omega)>-180\degree ∠ G ( j ω ) > − 1 8 0 °
따라서, crossover frequency 주변의 magnitude slope가 − 20 db/decade -20\text{db/decade} − 2 0 db/decade
Closed-Loop Frequency Response
Relation between bandwidth and crossover frequency
crossover frequency는 magnitude가 1이 되는 frequency의 크기를 의미하고 bandwidth는 closed-loop system의 응답성이 얼마나 되는지를 나타낸다.
∣ K G ( j ω ) ∣ ≫ 1 , for ω ≪ ω c ∣ K G ( j ω ) ∣ ≪ 1 , for ω ≫ ω c ∣ T ( j ω ) ∣ = ∣ K G ( j ω ) 1 + K G ( j ω ) ∣ ≅ { 1 , ω ≪ ω c , ∣ K G ( j ω ) ∣ , ω ≫ ω c |KG(j\omega)|\gg1,\; \text{for } \omega\ll\omega_c\\ |KG(j\omega)|\ll1,\; \text{for } \omega\gg\omega_c\\ |T(j\omega)|=\left|\cfrac{KG(j\omega)}{1+KG(j\omega)}\right|\cong \begin{cases} 1,\qquad\qquad\omega\ll\omega_c,\\ |KG(j\omega)|,\;\omega\gg\omega_c\\ \end{cases} ∣ K G ( j ω ) ∣ ≫ 1 , for ω ≪ ω c ∣ K G ( j ω ) ∣ ≪ 1 , for ω ≫ ω c ∣ T ( j ω ) ∣ = ∣ ∣ ∣ ∣ ∣ ∣ 1 + K G ( j ω ) K G ( j ω ) ∣ ∣ ∣ ∣ ∣ ∣ ≅ { 1 , ω ≪ ω c , ∣ K G ( j ω ) ∣ , ω ≫ ω c
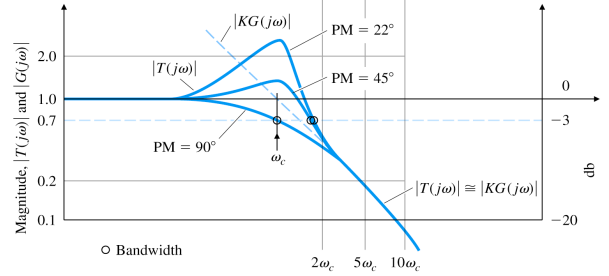
closed-loop system의 frequency가 crossover frequency보다 충분히 크거나 작았을 때의 값을 알았으니 그 사이의 값을 알아보면 다음과 같다.
crossover frequency ω c \omega_c ω c
{ P M = 90 ° → ∠ K G ( j ω c ) = − 90 ° → ∣ T ( j ω c ) ∣ = ∣ − j 1 1 − j 1 ∣ = 0.707 P M = 45 ° → ∠ K G ( j ω c ) = − 135 ° → ∣ T ( j ω c ) ∣ = ∣ − 2 2 − j 2 2 1 − 2 2 − j 2 2 ∣ = 1.31 \begin{cases} PM=90\degree\rightarrow\angle KG(j\omega_c)=-90\degree\rightarrow|T(j\omega_c)|=\left|\cfrac{-j1}{1-j1}\right|=0.707\\ PM=45\degree\rightarrow\angle KG(j\omega_c)=-135\degree\rightarrow|T(j\omega_c)|=\left|\cfrac{-\frac{\sqrt{2}}{2}-j\frac{\sqrt{2}}{2}}{1-\frac{\sqrt{2}}{2}-j\frac{\sqrt{2}}{2}}\right|=1.31 \end{cases} ⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ P M = 9 0 ° → ∠ K G ( j ω c ) = − 9 0 ° → ∣ T ( j ω c ) ∣ = ∣ ∣ ∣ ∣ ∣ ∣ 1 − j 1 − j 1 ∣ ∣ ∣ ∣ ∣ ∣ = 0 . 7 0 7 P M = 4 5 ° → ∠ K G ( j ω c ) = − 1 3 5 ° → ∣ T ( j ω c ) ∣ = ∣ ∣ ∣ ∣ ∣ ∣ 1 − 2 2 − j 2 2 − 2 2 − j 2 2 ∣ ∣ ∣ ∣ ∣ ∣ = 1 . 3 1 따라서, ω c ≤ ω B W ≤ 2 ω c \omega_c\leq\omega_{BW}\leq2\omega_c ω c ≤ ω B W ≤ 2 ω c
Compensation
PD Compensation
K D ( s ) = K ( T D s + 1 ) ( D ( 0 ) = 1 ) KD(s)=K(T_Ds+1)\;(D(0)=1) K D ( s ) = K ( T D s + 1 ) ( D ( 0 ) = 1 )
이렇게 된다면 고주파쪽 gain이 커지기 때문에 high frequency의 noise가 증폭될 수 있다.
Lead Compensation
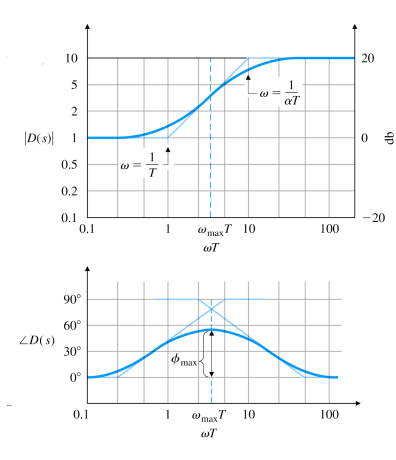
D ( s ) = T s + 1 α T s + 1 , where α < 1 ( D ( 0 ) = 1 ) D(s)=\cfrac{Ts+1}{\alpha Ts+1},\;\text{where }\alpha<1\;(D(0)=1) D ( s ) = α T s + 1 T s + 1 , where α < 1 ( D ( 0 ) = 1 ) ω max \omega_{\text{max}} ω max
Phase contribution :
ϕ = tan − 1 ( T ω ) − tan − 1 ( α T ω ) = tan − 1 ( T ω − α T ω 1 + T ω α T ω ) \begin{aligned}\phi &= \tan^{-1}(T\omega)-\tan^{-1}(\alpha T\omega)\\ &=\tan^{-1}\left(\cfrac{T\omega-\alpha T\omega}{1+T\omega\alpha T\omega}\right) \end{aligned} ϕ = tan − 1 ( T ω ) − tan − 1 ( α T ω ) = tan − 1 ( 1 + T ω α T ω T ω − α T ω ) Maximum ϕ \phi ϕ
ω max = 1 T α \omega_{\text{max}}=\cfrac{1}{T\sqrt{\alpha}} ω max = T α 1 Maximum phase conribution :
sin ϕ max = 1 − α 1 + α ⇒ α = 1 − sin ϕ max 1 + sin ϕ max \sin\phi_{\text{max}}=\cfrac{1-\alpha}{1+\alpha}\Rightarrow\alpha=\cfrac{1-\sin\phi_{\text{max}}}{1+\sin\phi_{\text{max}}} sin ϕ max = 1 + α 1 − α ⇒ α = 1 + sin ϕ max 1 − sin ϕ max lead compensation을할 때 maximum phase를 대략 60 ° 60\degree 6 0 °