Root Locus of a Basic Feedback System
Closed-loop transfer function : Y ( s ) R ( s ) = T ( s ) = D ( s ) G ( s ) 1 + D ( s ) G ( s ) H ( s ) \frac{Y(s)}{R(s)}=T(s)=\frac{D(s)G(s)}{1+D(s)G(s)H(s)} R ( s ) Y ( s ) = T ( s ) = 1 + D ( s ) G ( s ) H ( s ) D ( s ) G ( s )
Chacteristic equation : 1 + D ( s ) G ( s ) H ( s ) = 0 1+D(s)G(s)H(s)=0 1 + D ( s ) G ( s ) H ( s ) = 0 → a ( s ) + K b ( s ) = 0 → 1 + K L ( s ) = 0 ( L ( s ) : = b ( s ) / a ( s ) ) \rightarrow a(s)+Kb(s)=0\\ \rightarrow 1+KL(s)=0\;(L(s):=b(s)/a(s)) → a ( s ) + K b ( s ) = 0 → 1 + K L ( s ) = 0 ( L ( s ) : = b ( s ) / a ( s ) )
Root Locus : K를 0에서 ∞ \infty ∞
일반적인 상황에서 L ( s ) L(s) L ( s ) 1 + K L ( s ) = 0 , L ( s ) = b ( s ) a ( s ) 1+KL(s)=0,\; L(s)=\frac{b(s)}{a(s)} 1 + K L ( s ) = 0 , L ( s ) = a ( s ) b ( s )
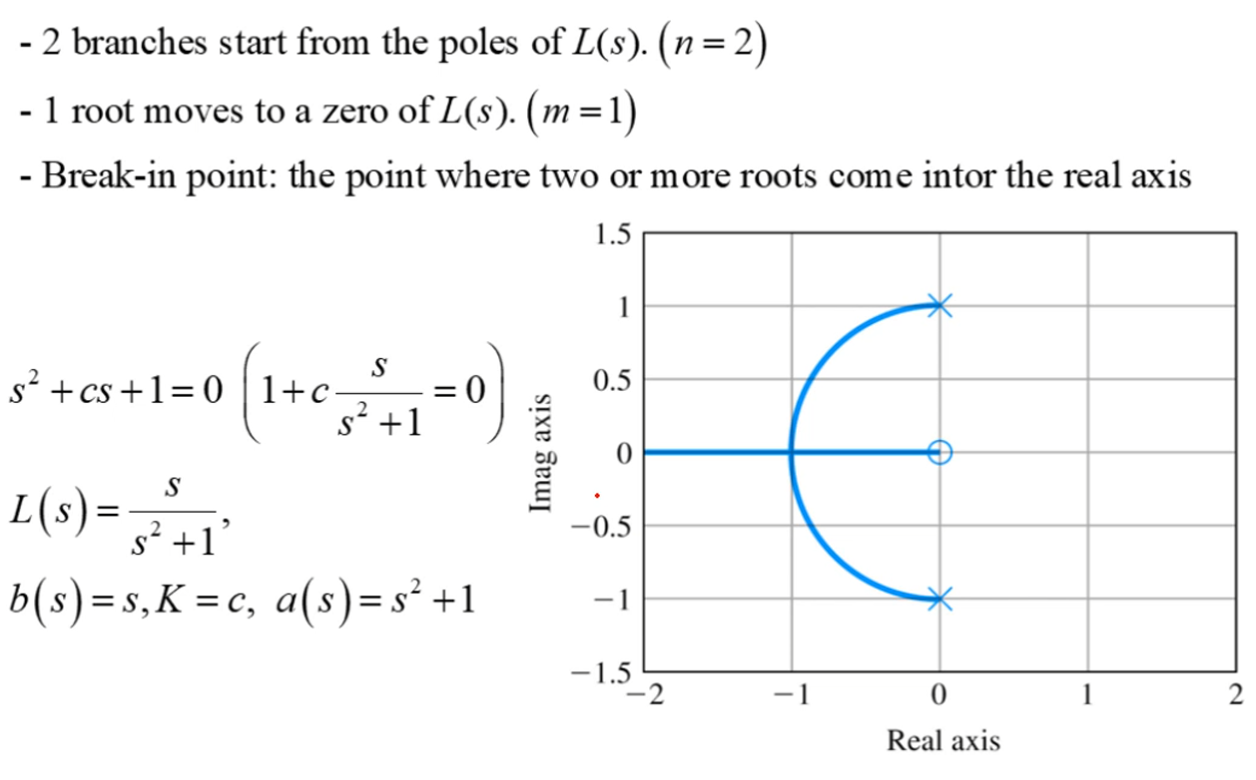
b ( s ) : z e r o o f L ( s ) a ( s ) : p o l e o f L ( s ) a ( s ) + K b ( s ) = ( s − r 1 ) ( s − r 2 ) ⋯ ( s − r i ) ( r i : c l o s e d − l o o p p o l e ) b(s) : zero\;of\;L(s)\\ a(s) : pole\;of\;L(s)\\ a(s)+Kb(s) = (s-r_1)(s-r_2)\cdots(s-r_i)\;\;(r_i : closed-loop\;pole) b ( s ) : z e r o o f L ( s ) a ( s ) : p o l e o f L ( s ) a ( s ) + K b ( s ) = ( s − r 1 ) ( s − r 2 ) ⋯ ( s − r i ) ( r i : c l o s e d − l o o p p o l e ) Root locus forms : 1 + K L ( s ) = 0 , 1 + K b ( s ) a ( s ) 1+KL(s)=0,\;1+K\frac{b(s)}{a(s)} 1 + K L ( s ) = 0 , 1 + K a ( s ) b ( s )
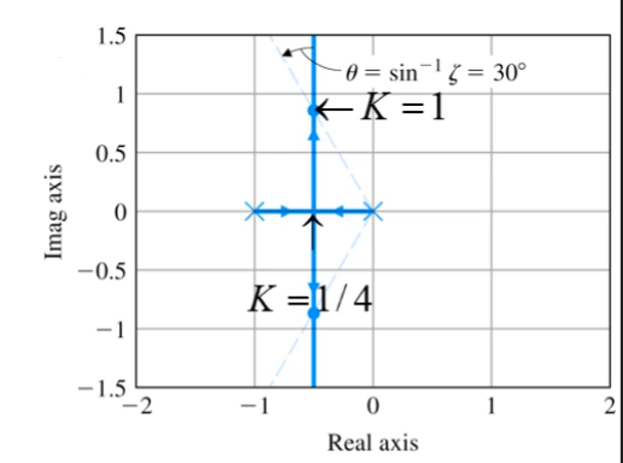
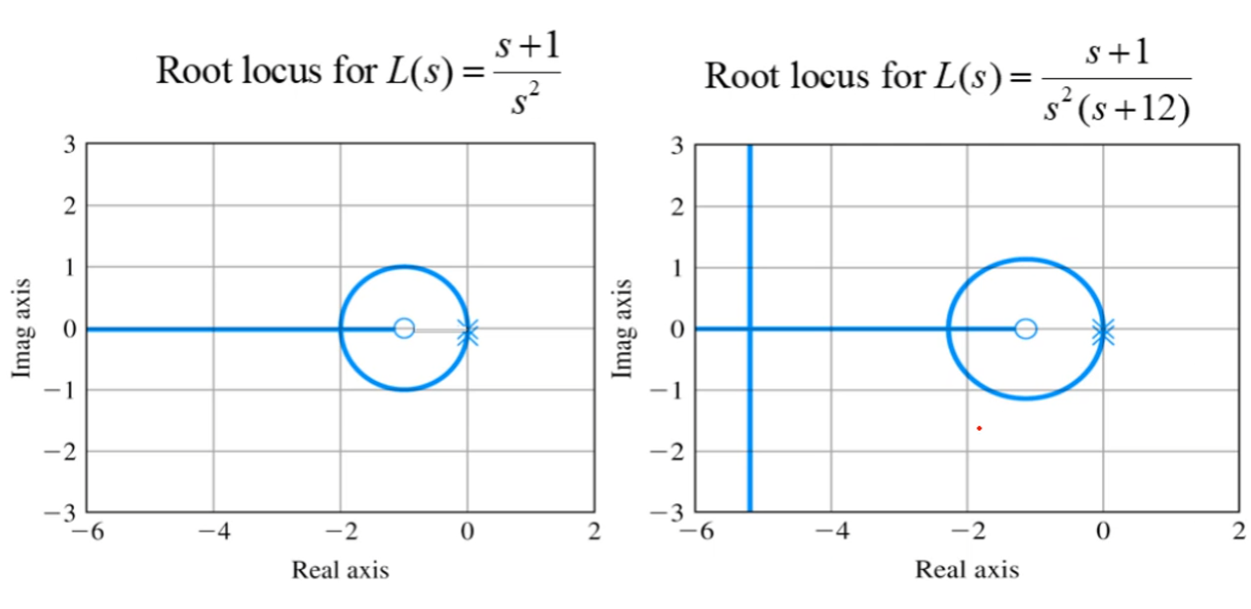
a ( s ) + K b ( s ) = 0 L ( s ) = b ( s ) a ( s ) = − 1 K a(s)+Kb(s)=0\\ L(s)=\frac{b(s)}{a(s)}=-\frac{1}{K} a ( s ) + K b ( s ) = 0 L ( s ) = a ( s ) b ( s ) = − K 1 root locus는 L ( s ) L(s) L ( s ) K = 0 K=0 K = 0 L ( s ) L(s) L ( s )
Guidelines for Sketching a Root Locus
L ( s ) L(s) L ( s ) L ( s ) = − 1 / K L(s)=-1/K L ( s ) = − 1 / K
L ( s ) = Π i = 1 m ( s − z i ) Π i = 1 n ( s − p i ) = − 1 K → ∠ L ( s ) = ∑ [ ∠ ( s − z i ) ] − ∑ [ ∠ ( s − p i ) ] = ∑ ψ i − ∑ ϕ i = 180 ° + 360 ° ( l − 1 ) [ 0 ° + 360 ° ( l − 1 ) f o r K < 0 ] \begin{aligned} L(s)=\frac{\Pi_{i=1}^{m}(s-z_i)}{\Pi_{i=1}^{n}(s-p_i)} &= -\frac{1}{K}\rightarrow\angle L(s)=\sum[\angle(s-z_i)]-\sum[\angle(s-p_i)]\\ &= \sum\psi_i-\sum\phi_i=180\degree+360\degree(l-1)[0\degree+360\degree(l-1)\;for\;K<0] \end{aligned} L ( s ) = Π i = 1 n ( s − p i ) Π i = 1 m ( s − z i ) = − K 1 → ∠ L ( s ) = ∑ [ ∠ ( s − z i ) ] − ∑ [ ∠ ( s − p i ) ] = ∑ ψ i − ∑ ϕ i = 1 8 0 ° + 3 6 0 ° ( l − 1 ) [ 0 ° + 3 6 0 ° ( l − 1 ) f o r K < 0 ] Rules for Determining a Positive(180° \degree °
Root Locus를 손으로 그리는 방법
RULE 1 : n개의 branch가 L ( s ) L(s) L ( s )
RULE 2 : 실수축에 내가 보고자 하는 점이 있고 그 오른쪽에 pole의 갯수가 홀수개 있다면 그 점은 root locus 위에 있다.
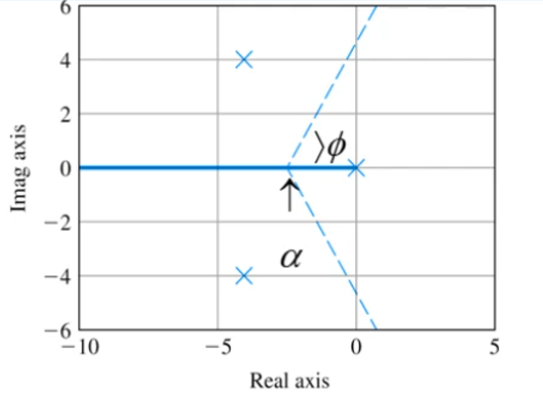
RULE 3 : K가 매우 클 때, n − m n-m n − m s = α s=\alpha s = α ϕ l \phi_l ϕ l
ϕ l = 180 ° + 360 ° ( l − 1 ) n − m , l = 1 , 2 , … , n − m ( Angles of asymptotes ) α = ∑ p i − ∑ z i n − m , ( Center of asymptotes ) \phi_l=\frac{180\degree+360\degree(l-1)}{n-m},\quad l=1,2,\dots,n-m\quad(\text{Angles of asymptotes})\\ \alpha=\frac{\sum p_i-\sum z_i}{n-m},\qquad (\text{Center of asymptotes}) ϕ l = n − m 1 8 0 ° + 3 6 0 ° ( l − 1 ) , l = 1 , 2 , … , n − m ( Angles of asymptotes ) α = n − m ∑ p i − ∑ z i , ( Center of asymptotes )
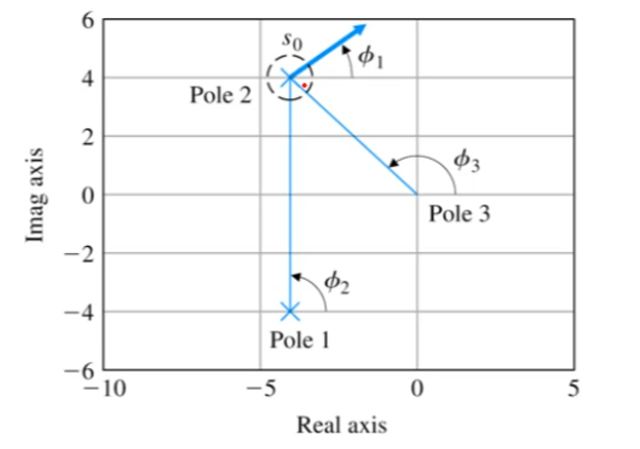
RULE 4 : 한 점에 pole이 1개 이상 있을 때, pole에서 시작하는 선의 각도는 몇 도 일까?(multiplicity q q q
q ϕ l , d e p = ∑ ψ i − ∑ i ≠ j ϕ i − 180 ° − 360 ° ( l − 1 ) q ψ l , a r r = ∑ ϕ i − ∑ i ≠ j ψ i + 180 ° − 360 ° ( l − 1 ) q\phi_{l,dep}=\sum\psi_i-\sum_{i\neq j}\phi_i-180\degree-360\degree(l-1)\\ q\psi_{l,arr}=\sum\phi_i-\sum_{i\neq j}\psi_i+180\degree-360\degree(l-1) q ϕ l , d e p = ∑ ψ i − i = j ∑ ϕ i − 1 8 0 ° − 3 6 0 ° ( l − 1 ) q ψ l , a r r = ∑ ϕ i − i = j ∑ ψ i + 1 8 0 ° − 3 6 0 ° ( l − 1 )
RULE 5 : locus에서 두 선이 만나는 mulitple roots point는 다음과 같다. ( b d a d s − a d b d s ) = 0 (b\frac{da}{ds}-a\frac{db}{ds})=0 ( b d s d a − a d s d b ) = 0 180 ° + 360 ° ( l − 1 ) q \frac{180\degree+360\degree(l-1)}{q} q 1 8 0 ° + 3 6 0 ° ( l − 1 )
Continuation locus : 여러 roots의 점에서부터 도착하는 각도를 계산하는 것을 말한다. K = K 1 + K 2 K = K_1+K_2 K = K 1 + K 2 K 2 K_2 K 2
a ( s ) + K b ( s ) = a ( s ) + ( K 1 + K 2 ) b ( s ) = ( a ( s ) + K 1 b ( s ) ) + K 2 b ( s ) multiple poles at K = K 1 → { K 2 > 0 : angle of departure from multiple poles K 2 < 0 : angle of arrival to multiple pole a(s)+Kb(s)=a(s)+(K_1+K_2)b(s)=(a(s)+K_1b(s))+K_2b(s)\\ \text{multiple poles at }K=K_1\rightarrow\begin{cases}K_2>0:\text{angle of departure from multiple poles}\\K_2<0:\text{angle of arrival to multiple pole}\end{cases} a ( s ) + K b ( s ) = a ( s ) + ( K 1 + K 2 ) b ( s ) = ( a ( s ) + K 1 b ( s ) ) + K 2 b ( s ) multiple poles at K = K 1 → { K 2 > 0 : angle of departure from multiple poles K 2 < 0 : angle of arrival to multiple pole Selecting the Parameter Value
특정 K값을 정하게 되면 그 상황에 대한 system의 dynamic response를 알 수 있다.K = − 1 L ( s ) or K = 1 ∣ L ( s ) ∣ K=-\frac{1}{L(s)}\text{ or }K=\frac{1}{|L(s)|} K = − L ( s ) 1 or K = ∣ L ( s ) ∣ 1
Dominant poles : 다른 pole에 비해 허수축에 가까운 pole을 의미한다. 이 pole이 이 시스템의 응답을 좌지우지할 수 있다.
PD control의 단점 : 아날로그 신호는 sin wave와 같은 noise가 들어오게 된다. 이를 미분을 하게 되면 이 noise도 같이 증폭되어 들어오는 상황을 만들 수 있어서 결국 시스템에 영향을 줄 수 있다. 이를 극복하고자 lead compensator를 사용하여 controller를 만든다.
lead compensator : K s + z s + p ( 0 < z < p ) K\frac{s+z}{s+p}(0<z<p) K s + p s + z ( 0 < z < p )
Design Using Dynamic Compensation
Lead compensation
D ( s ) = K s + z s + p , z < p ≈ P D c o n t r o l ( k P + k D s ) D(s)=K\frac{s+z}{s+p}, z<p\\ \approx PD\;control\;(k_P+k_Ds) D ( s ) = K s + p s + z , z < p ≈ P D c o n t r o l ( k P + k D s ) 응답성을 높이기 위해 rise time을 줄이고 overshoot을 줄인다.(감쇠비를 키운다.)
Lead compensation을 설정하는 방법은 많지만 2가지 정도만 알아보자.
Lag compensation
D ( s ) = K s + z s + p , z > p ≈ P I c o n t r o l ( k P + k I 1 s ) D(s)=K\frac{s+z}{s+p}, z>p\\ \approx PI\;control\;(k_P+k_I\frac{1}{s}) D ( s ) = K s + p s + z , z > p ≈ P I c o n t r o l ( k P + k I s 1 ) zero가 충분히 크다면 pole을 무시할 수 있어 PI control과 유사하게 보일 수 있다.
Notch compensation
light damped를 만들어서 안정적으로 작동하게 한다.
ex) Design of Lead Compensation [trial & error]
Plant : G ( s ) = 1 s ( s + 1 ) G(s)=\frac{1}{s(s+1)} G ( s ) = s ( s + 1 ) 1 M p ≤ 20 % , t r ≤ 0.3 s e c M_p\leq 20\%,\;t_r \leq0.3\;sec M p ≤ 2 0 % , t r ≤ 0 . 3 s e c
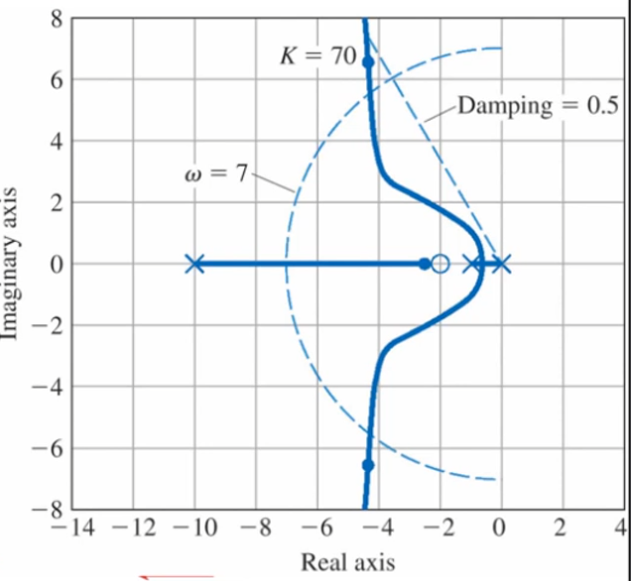
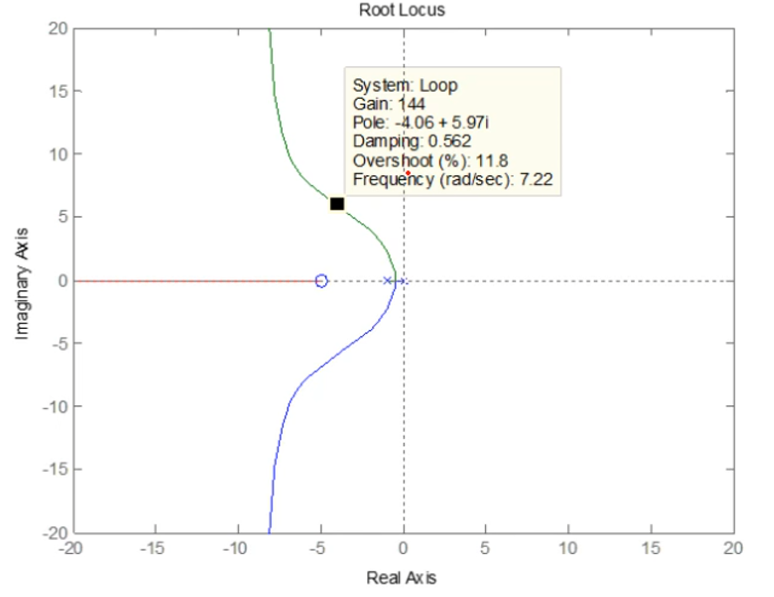
→ ζ ≥ 0.5 , ω n ≅ 1.8 / 0.3 ≅ 6 → Set ζ ≥ 0.5 , ω m ≅ 7 ( margin ) \rightarrow \zeta \geq0.5,\;\omega_n\cong1.8/0.3\cong6\rightarrow\text{Set }\zeta\geq0.5,\;\omega_m\cong7(\text{margin}) → ζ ≥ 0 . 5 , ω n ≅ 1 . 8 / 0 . 3 ≅ 6 → Set ζ ≥ 0 . 5 , ω m ≅ 7 ( margin ) Lead Compensation : D ( s ) = K s + 2 s + 10 D(s)=K\frac{s+2}{s+10} D ( s ) = K s + 1 0 s + 2
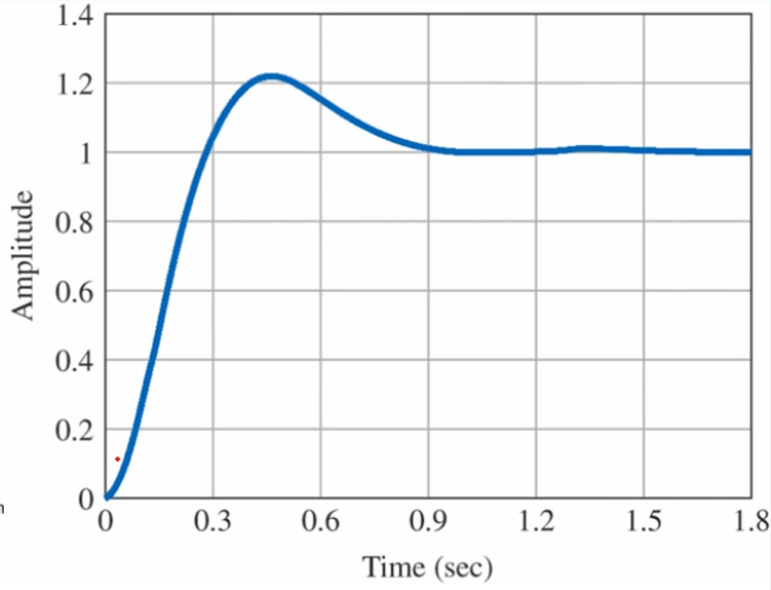
( ϕ l = ± 90 ° , α = − 4.5 ) K = 70 → ζ = 0.56 , ω n = 7.7 rad/sec (\phi_l=\pm90\degree,\quad\alpha=-4.5)\\ K=70\rightarrow\zeta=0.56,\;\omega_n=7.7\text{ rad/sec} ( ϕ l = ± 9 0 ° , α = − 4 . 5 ) K = 7 0 → ζ = 0 . 5 6 , ω n = 7 . 7 rad/sec Poles : ζ ω n ( = − 4.3 ) ± j ω \zeta\omega_n(=-4.3)\pm j\omega ζ ω n ( = − 4 . 3 ) ± j ω
− 0 − 1 − 10 = − 4.3 − 4.3 + r 3 → r 3 = − 2.4 -0-1-10=-4.3-4.3+r_3\rightarrow r_3=-2.4 − 0 − 1 − 1 0 = − 4 . 3 − 4 . 3 + r 3 → r 3 = − 2 . 4 pole은 -2.4로 zero에 가까이에 놓여 있다.
Design of Lead compensation [Method 1]
Plant : G ( s ) = 1 s ( s + 1 ) G(s)=\frac{1}{s(s+1)} G ( s ) = s ( s + 1 ) 1 M p ≤ 20 % , t r ≤ 0.3 s e c M_p\leq 20\%,\;t_r \leq0.3\;sec M p ≤ 2 0 % , t r ≤ 0 . 3 s e c
→ ζ ≥ 0.5 , ω n ≅ 1.8 / 0.3 ≅ 6 → Set ζ ≥ 0.5 , ω m ≅ 7 ( margin ) \rightarrow \zeta \geq0.5,\;\omega_n\cong1.8/0.3\cong6\rightarrow\text{Set }\zeta\geq0.5,\;\omega_m\cong7(\text{margin}) → ζ ≥ 0 . 5 , ω n ≅ 1 . 8 / 0 . 3 ≅ 6 → Set ζ ≥ 0 . 5 , ω m ≅ 7 ( margin ) Lead compensation : D ( s ) = K s + 7 s + 21 D(s)=K\frac{s+7}{s+21} D ( s ) = K s + 2 1 s + 7
Lead compensation : D ( s ) = K s + 5 s + 21 D(s)=K\frac{s+5}{s+21} D ( s ) = K s + 2 1 s + 5
Design of Lead Compensation [Method 2]
Plant : G ( s ) = 1 s ( s + 1 ) G(s)=\frac{1}{s(s+1)} G ( s ) = s ( s + 1 ) 1
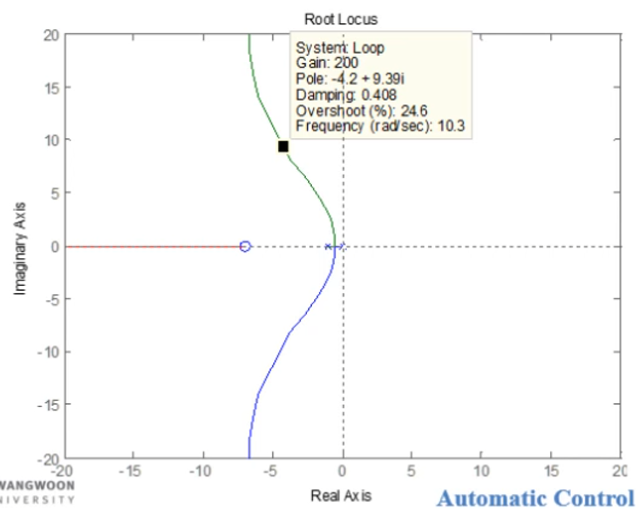
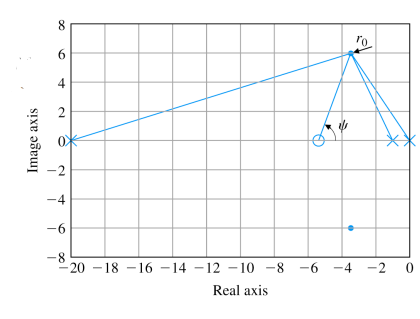
closed loop poles at r 0 = − 3.5 + j 3.5 3 r_0=-3.5+j3.5\sqrt{3} r 0 = − 3 . 5 + j 3 . 5 3
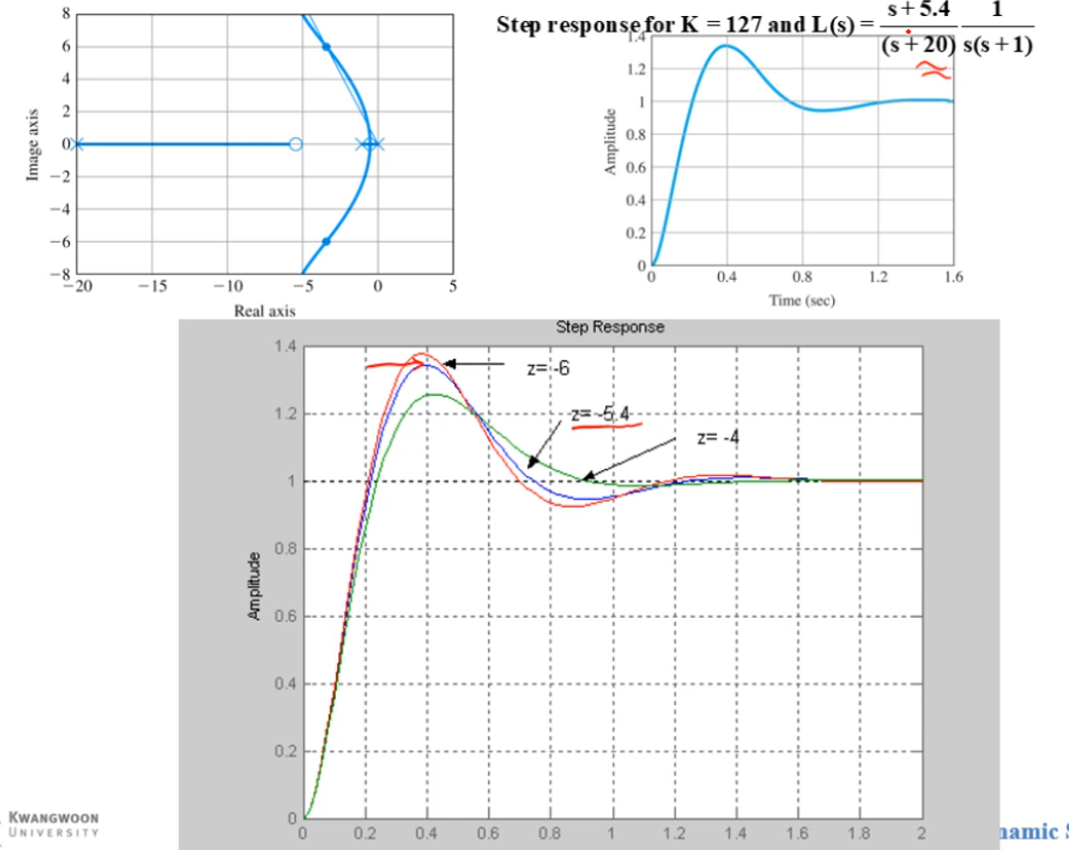
p ≤ 20 ( noise suppression requirement ) p\leq20\;(\text{noise suppression requirement}) p ≤ 2 0 ( noise suppression requirement ) ∠ ( G ( s ) 1 s + p ) = 107.4 ° at r 0 = − 3.5 + j 3.5 3 → Angle ψ from the lead zero = 72.6 ° → z = − 5.4 \angle(G(s)\frac{1}{s+p})=107.4\degree\;\text{at } r_0=-3.5+j3.5\sqrt{3}\\ \rightarrow\text{Angle }\psi\text{ from the lead zero}=72.6\degree\\ \rightarrow z=-5.4 ∠ ( G ( s ) s + p 1 ) = 1 0 7 . 4 ° at r 0 = − 3 . 5 + j 3 . 5 3 → Angle ψ from the lead zero = 7 2 . 6 ° → z = − 5 . 4 K = 127 K=127 K = 1 2 7 → D ( s ) = 127 s + 5.4 s + 20 \rightarrow D(s)=127\frac{s+5.4}{s+20} → D ( s ) = 1 2 7 s + 2 0 s + 5 . 4
overshoot가 20%보다 크므로 fine tuning을 통해 수정하여 사용한다.
Design Using Lag Compensation
Dynamic response는 만족하지만 steady state error가 만족스럽지 않은 경우를 생각해 보자. 이는 low-frequency gain(K p , K v , e t c K_p,\;K_v,\;etc K p , K v , e t c ω n \omega_n ω n s = 0 s=0 s = 0
D ( s ) = K s + z s + p , z > p z , p ≪ ω n D(s)=K\frac{s+z}{s+p},\;z>p\\ z,p\ll\omega_n D ( s ) = K s + p s + z , z > p z , p ≪ ω n 즉, compenstor의 zero와 pole을 원점에 가깝게 두면 dynamic response에서는 영향이 크게 없지만, s = 0 s=0 s = 0
ex)
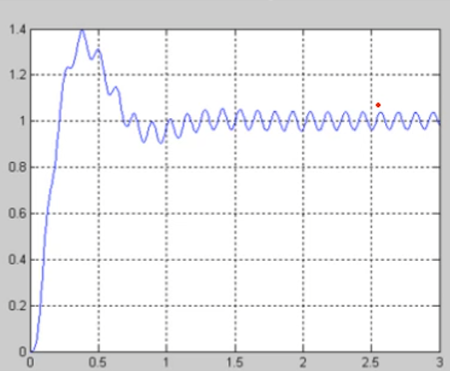
G ( s ) = 1 s ( s + 1 ) , D ( s ) = 91 ( s + 2 ) s + 13 G(s)=\frac{1}{s(s+1)},\quad D(s)=\frac{91(s+2)}{s+13} G ( s ) = s ( s + 1 ) 1 , D ( s ) = s + 1 3 9 1 ( s + 2 ) Velocity constant : K v = lim s → 0 s K D G = lim s → 0 s ( 91 ) s + 2 s + 13 1 s ( s + 1 ) = 14 K_v=\lim_{s\rightarrow0}sKDG=\lim_{s\rightarrow0}s(91)\frac{s+2}{s+13}\frac{1}{s(s+1)}=14 K v = lim s → 0 s K D G = lim s → 0 s ( 9 1 ) s + 1 3 s + 2 s ( s + 1 ) 1 = 1 4
root locus의 변화가 거의 없는 상태에서 K v K_v K v K v = 70 K_v=70 K v = 7 0
lag compensation :
D 2 ( s ) = s + z s + p , z > p , set z and p small → D 2 ( s ) = s + 0.05 s + 0.01 D_2(s)=\frac{s+z}{s+p},\quad z>p,\\ \text{set z and p small}\\ \rightarrow\qquad D_2(s)=\frac{s+0.05}{s+0.01} D 2 ( s ) = s + p s + z , z > p , set z and p small → D 2 ( s ) = s + 0 . 0 1 s + 0 . 0 5 이렇게 되면 dynamic response에는 변화가 없고 steady state error만 줄일 수 있다.
Design Using Notch Compensation
Lead and lag compensation : K D ( s ) = 91 s + 2 s + 13 s + 0.05 s + 0.01 KD(s)=91\frac{s+2}{s+13}\frac{s+0.05}{s+0.01} K D ( s ) = 9 1 s + 1 3 s + 2 s + 0 . 0 1 s + 0 . 0 5
Plant transfer function uncluding the effect of flexibility :
G ( s ) = 2500 s ( s + 1 ) ( s 2 + s + 2500 ) = 1 s ( s + 1 ) 2500 s 2 + s + 2500 G(s)=\frac{2500}{s(s+1)(s^2+s+2500)}=\frac{1}{s(s+1)}\frac{2500}{s^2+s+2500} G ( s ) = s ( s + 1 ) ( s 2 + s + 2 5 0 0 ) 2 5 0 0 = s ( s + 1 ) 1 s 2 + s + 2 5 0 0 2 5 0 0 진동을 포함한 plant에 대해서 compensation이 추가된 root locus를 그리게 되면 다음과 같다.
Notch filter를 사용해서 oscillation을 억제한다.
D n o t c h ( s ) = s 2 + 2 ζ ω o s + ω o 2 ( s + ω o ) 2 D_{notch}(s)=\frac{s^2+2\zeta\omega_os+\omega_o^2}{(s+\omega_o)^2} D n o t c h ( s ) = ( s + ω o ) 2 s 2 + 2 ζ ω o s + ω o 2