Regularization (정형화, 규제, 일반화)이란
모델이 과적합되게 학습하지 않고 일반성을 가질 수 있도록 규제 하는 것을 말합니다.
데이터의 피쳐를 손대지 않고 제너럴하게 만드려면 기울기(가중치)를 건드리면 안되고 사용하는 것이 Lasso와 Ridge입니다.
Lasso
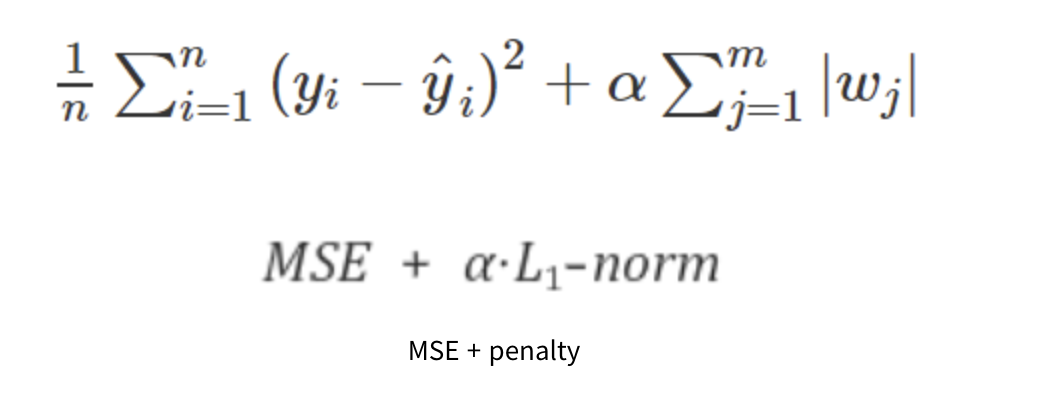
w는 가중치를 의미합니다.
MSE에 알파를 곱한 L1규제항을 더한 것입니다. (알파를 하이퍼파라미터로 정도를 정할 수 있음.)
학습의 방향이 단순히 손실함수를 줄여나가는 것 뿐만 아니라 가중치값들 또한 최소가 될 수 있도록 진행됩니다.
알파는 하이퍼파라미터인데

알파를 높이면, 전체 패널티값이 줄어드니 가중치의 합도 줄어들도록 학습합니다.
즉 계속해서 특정 상수의 값을 빼내가는 것이므로 몇몇 가중치들은 0에 수렴하고 feature의 수도 감소하게됩니다.
궁극적으로 구불구불한 그래프를 피쳐수를 줄여 펴주는 것이죠.
가중치가 0인 중요하지 않은 특성들을 제외해줌으로써 모델에서 중요한 특성이 무엇인지 알 수 있게됩니다.
반대로 알파를 줄이면
상대적으로 많은 피쳐를 사용하게 되므로 과적합 우려가 있습니다.
Ridge
모델의 복잡도를 조정합니다.
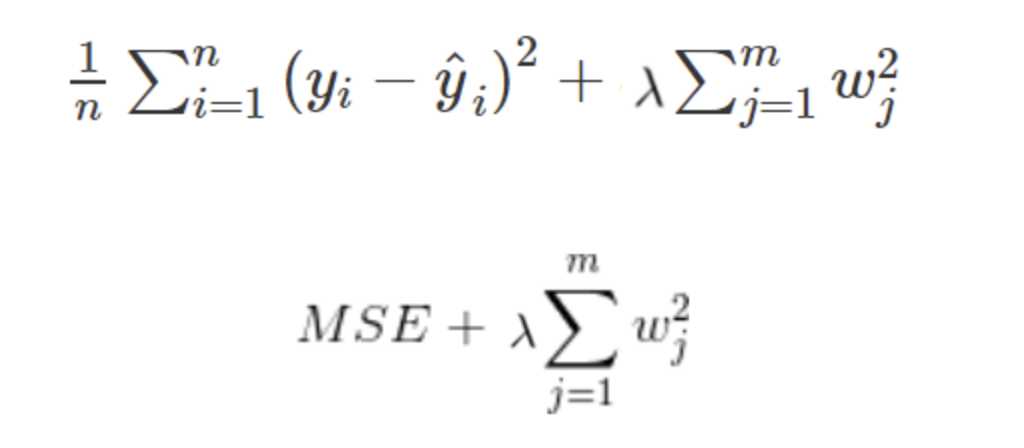
라쏘와 비슷하게 기존 손실함수에 L2항을 추가한 형태입니다.
미분값의 음수를 취하면 각 항의 부호가 바뀌므로 가중치가 양수일 땐 L2패널티가 음수, 가중치가 음수일 땐 L2 패널티가 양수가 되어 가중치를 0의 방향으로 잡아당기는 역할을 합니다.
즉, 가중치의 절대값을 가능한 작게 만드려는 작업을 하는 것입니다.
이를 weight decay라고 하며 weight decay는 특정 가중치가 비이상적으로 커지고 그것이 학습 효과에 큰 영향을 주는 것을 방지할 수 있습니다.
여기서도 중요한 것은 바로 람다(λ)입니다.
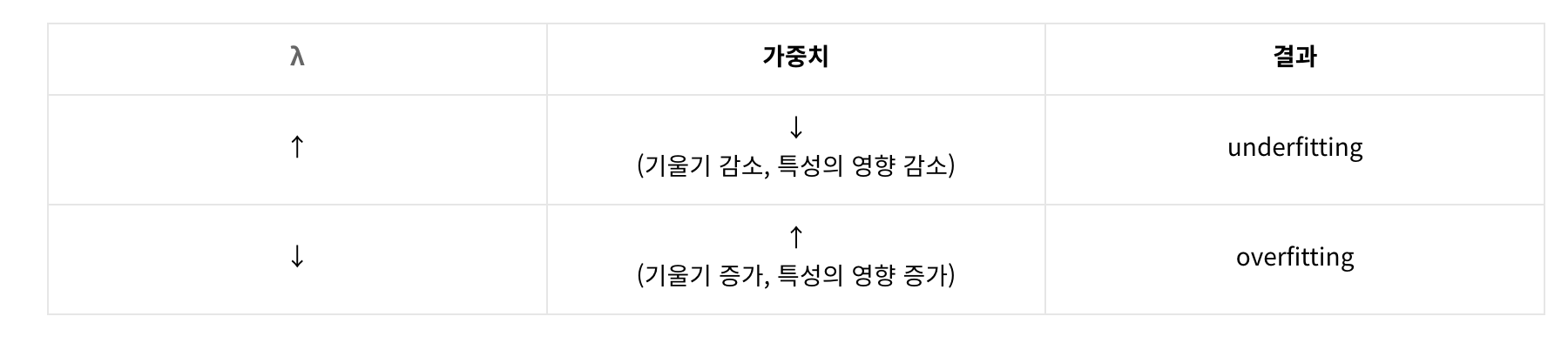
비교

