모델 성능 평가란
모델 선능평가란, 실제 모델과 모델의 예측값을 비교하여 오차를 구하는 것입니다.
실제값-예측값=0이라면 모델이 100% 맞춘 것이겠죠.
하지만 실제 모델이 그러기는 힘들고 오차를 구해서 어느정도까지의 오차를 허용할 것인지 결정하게됩니다.
모델 평가를 하는 목적은 과적합을 방지하고 제너럴하면서 최적의 모델을 찾기위함입니다.
모델 성능평가는 결과변수가 있어야 잘한건지 아닌지 확인할 수 있기 때문에 지도학습에서만 사용할 수 있습니다.
평가지표는 다양하며 모델링의 목적, 목표변수의 유형에 따라 다른 평가지표를 사용합니다.
Traingin과 Validation값이 거의 일치해야 좋은 모델이며, Training 성능이 좋은데 Validation 성능이 떨어지면 과적합입니다....
평가지표 분류
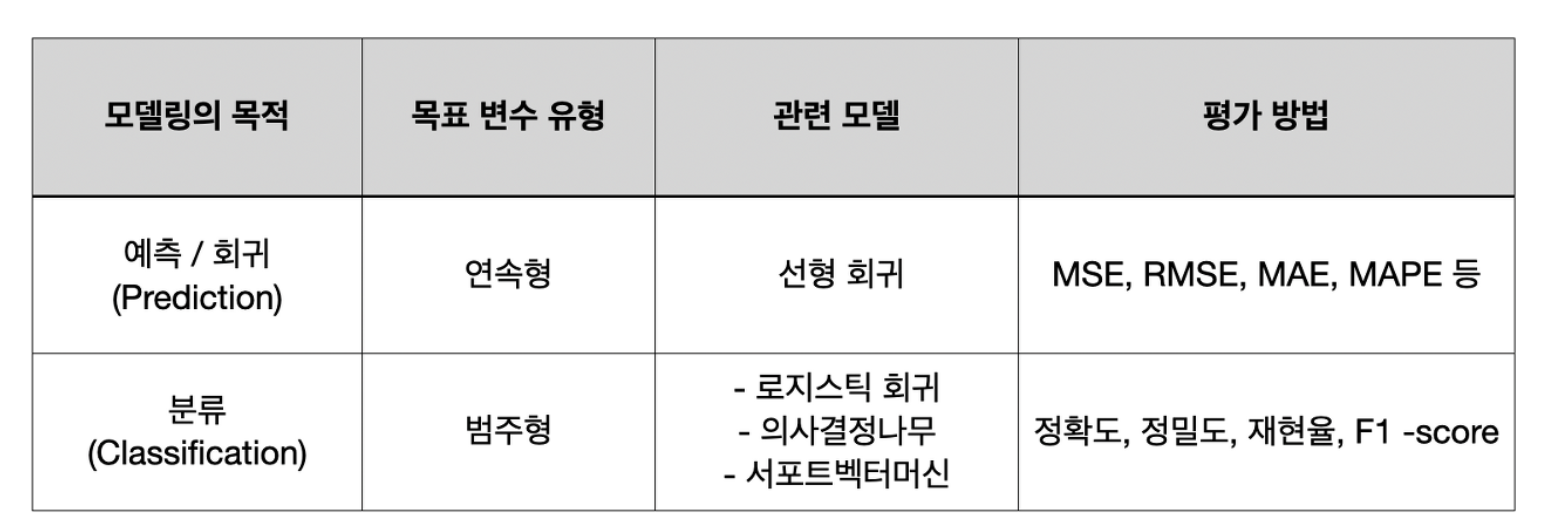
1. Prediction 성능평가
회귀 모델의 평가 지표에 대해 알아보자, 이 평가지표는 오차에 대해 평가하므로 값이 작을수록 모델의 성능이 좋다는 것을 의미합니다.
MSE(Mean Squared Error : 평균 제곱 오차)
실제값과 예측값의 차이를 제곱해서 평균한 것
특이값이 존재하면 수치가 많이 늘어난다.
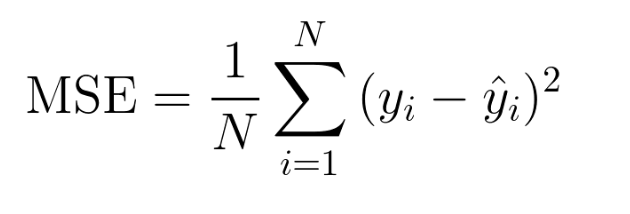
from sklearn.metrics import mean_squared_error
MSE = mean_squared_error(y, y_pred)RMSE(Root Mean Squared Error : 평균 제곱근 오차)
MSE값은 오류의 제곱을 구하므로 실제 오류의 평균보다 값이 더 커지는 특성이 있으므로, MSE에 루트를 씌운 것입니다.
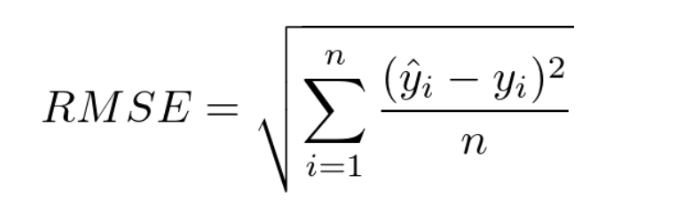
이는 sklearn에서 제공하지 않아. MSE에 0.5를 곱하여 사용합니다.
from sklearn.metrics import mean_squared_error
RMSE = mean_squared_error(y, y_pred)**0.5MAE (Mean Absoulte Error: 평균 제곱근 오차)
실제값과 예측값의 차이를 절대값으로 변환해 평균한 것
mae는 에러에 절대값을 취하기 때문에 에러의 크기가 그대로 반영됩니다.
에러에 따른 손실이 선형적으로 올라갈 때 적합하며 이상치가 많을 때 주로 사용됩니다.
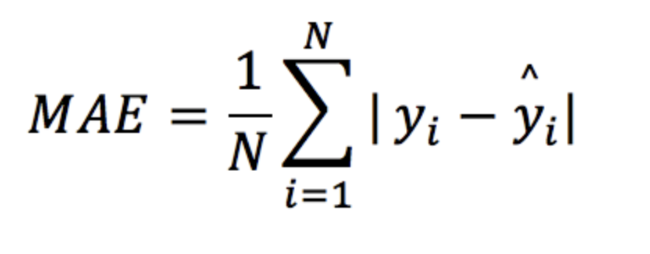
from sklearn.metrics import mean_absolute_error
mean_absolute_error(y_test, y_pred)MAPE (Mean Absolute Percentage Error : 평균 절대비율 오차)
MSE, RMSE의 단점을 보완한 평가지표.
MAE를 퍼센트로 변환한 것.
모델에 대한 편향이 존재합니다.
def MAPE(y_test, y_pred):
return np.mean(np.abs((y_test - y_pred) / y_test)) * 100
MAPE(y_test, y_pred)2. Classification 모델 성능 평가
분류 모델의 평가방법도 회귀 모형과 비슷하게 실제 데이터와 예측 결과 데이터가 얼마나 서로 비슷한가에 기반하지만, 단순히 이것만 가지고 판단하기에는 무리가 있습니다.
오차 행렬 (confusion Matrix)
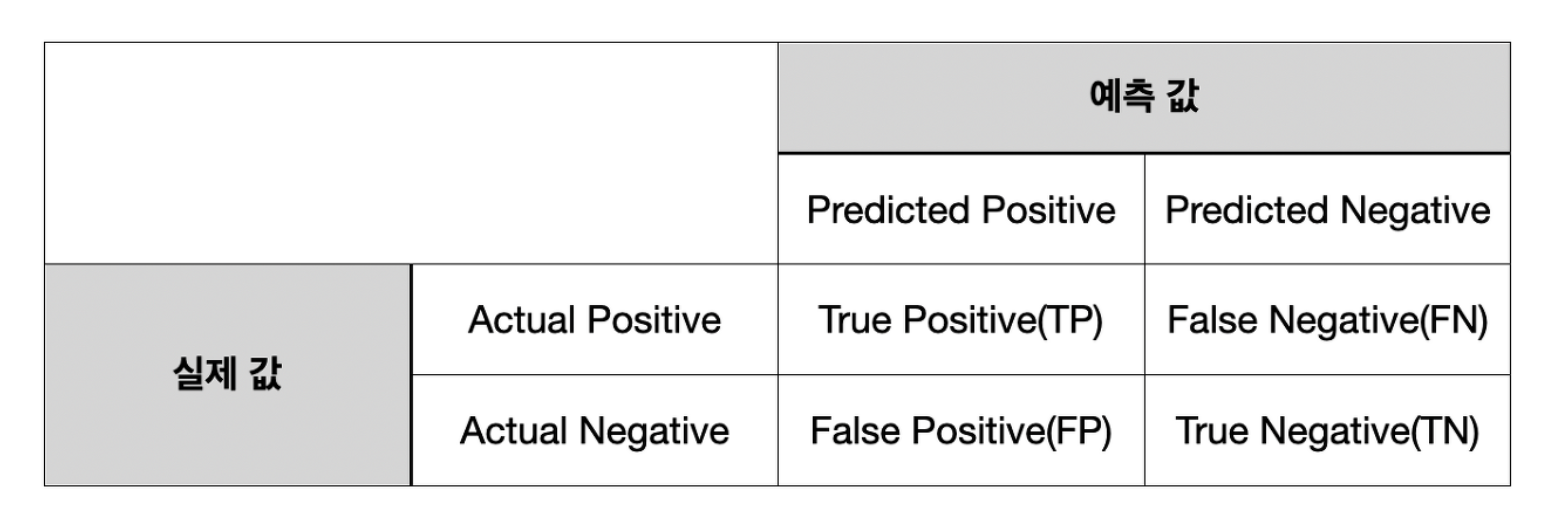
오차 행렬은 분류의 예측 범주와 실제 데이터의 분류 범주를 교차 표 형태로 정리한 행렬입니다.
뿐만 아니라 이진 분류의 예측 오류가 얼마인지와 더불어 어떠한 유형의 예측 오류가 발생하고 있는지 함께 나타냅니다.
from sklearn.metrics import confusion_matrix, classification_report, accuracy_score
confusion_matrix(y_pred, y_test)정확도 (Accuracy)
전체 데이터 중에 정확하게 예측한 데이터의 수
정확도는 불균형한 데이터의 경우 정확도는 적합한 평가지표가 아닙니다.
따라서 불균형한 데이터는 imbalanced data작업을 거치러나 다른 평가지표를 사용하는 것이 적합합니다.
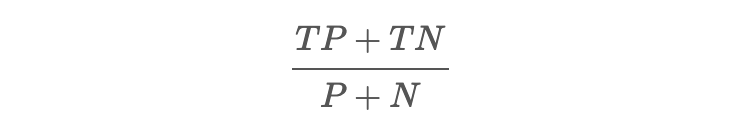
from sklearn.metrics import confusion_matrix, classification_report, accuracy_score
accuracy_score(y_pred, y_test)정밀도 (precision)
정밀도는 T로 판단한 것 중 진짜 T의 비율입니다.

재현률 (Recall) = 민감도 (Sensitivity)
실제값이 True인 관측치 중 예측치가 적중한 정도
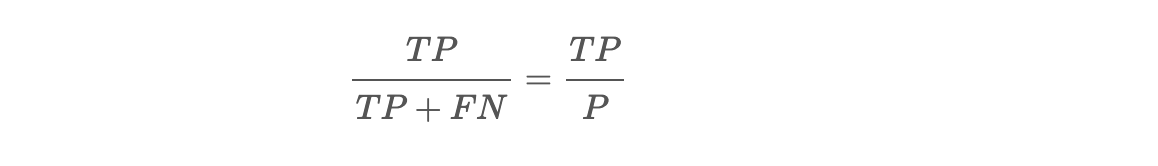
정밀도와 재현률을 positive 데이터 셋 예측 성능에 좀 더 초점을 맞춘 평가 지표이며, 이진 분류 모델의 업무 특성에 따라 특정 평가 지표가 더 중요한 지표로 간주될 수 있습니다.
가령, 재현율은 "실제 양성이 데이터 예측을 음성으로 잘못 판단하게 되면 업무 상 큰 영향이 발생하는 경우 더 중요한 지표로 간주"되고, 정밀도는 "실제 음성인 데이터를 양성으로 잘못 판단하게 되었을 때 큰 문제가 발생되는 경우" 더 중요한 지표로 간주됩니다.
재현율과 정밀도 모두 TP를 높이는 데 초점이지만 사실,
재현율을 FN 낮추기, 정밀도는 FP 낮추기에 초점을 둡니다.
이러한 특성 때문에 재현율과 정밀도는 서로 보완적인 지표로 trade-off 관계입니다.
ROC Curve
재현률과 정밀도의 관계가 보이는 양상을 2차원 평면상에 그려낸 것입니다.
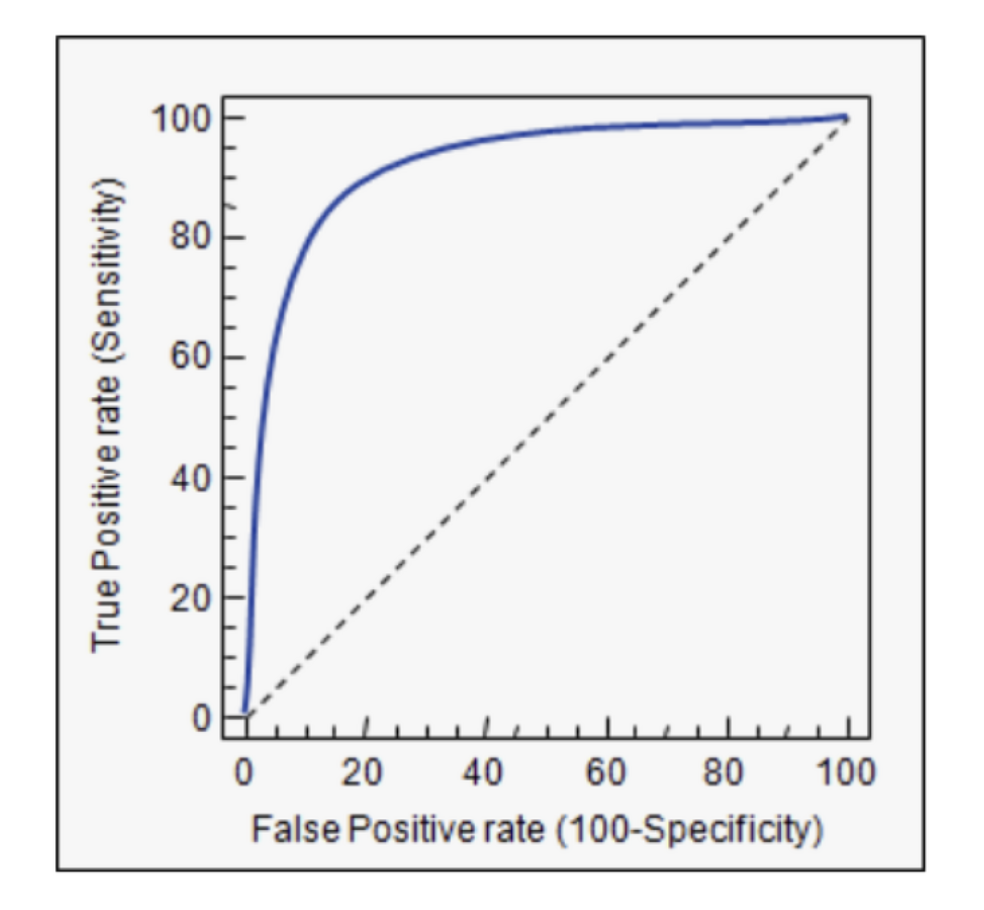
위 그림에서 파란색 곡선이 바로 ROC이고, ROC Curve 면적을 AUC라고 하며 1일 수록 좋은 모델입니다.
F1 Score
F1 Score는 정밀도와 재현율을 결합(조화 평균)하여 만든 지표로 정밀도와 재현율이 어느 한쪽으로 치우치지 않는 수치를 나타낼 때 F1 Score는 높은 값을 가지게 됩니다.
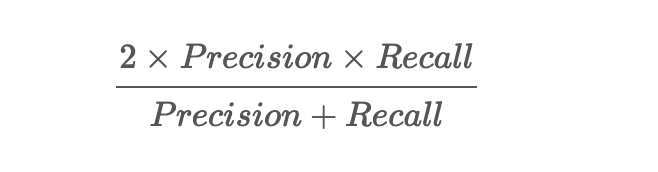
정확도, 정밀도, 재현율, F1-score는 모두 0~1 사이의 값을 가지며, 1에 가까울수록 성능이 좋다는 것을 의미합니다.