Axioms of Probability

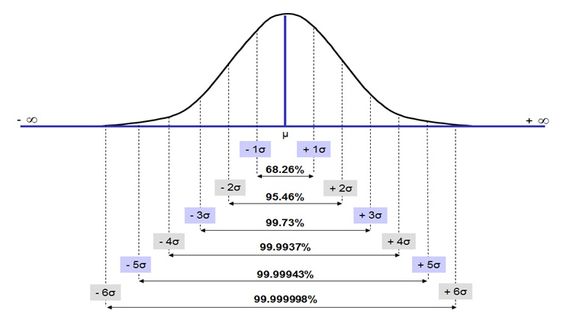
Sample Space and Events

Discrete Sample Space(이산형 표본공간)

Continuous Sample Space(연속형 표본공간)

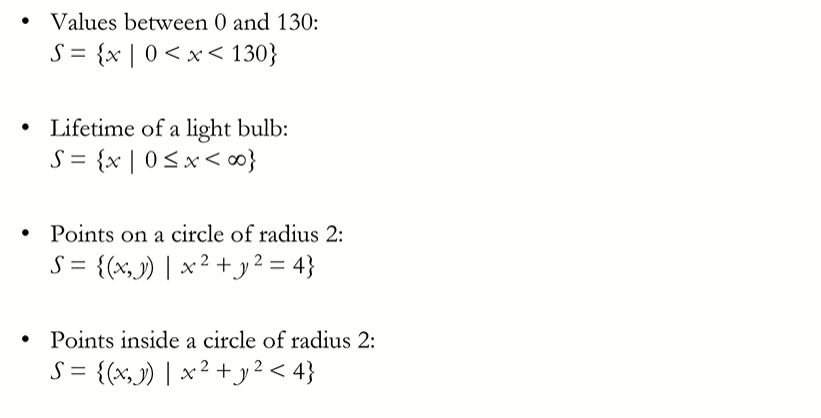
Events(사건)

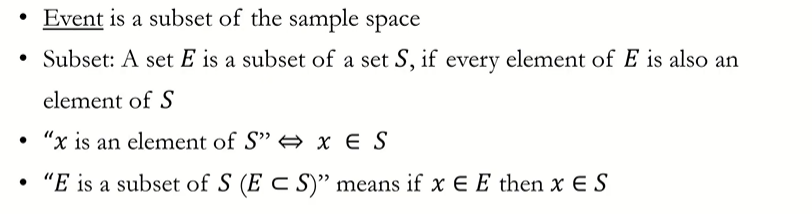
Events - Example

A : Event
odd number = 홀수

Example - Sample Space, Events

E = Sample State의 부분집합
S = Sample State

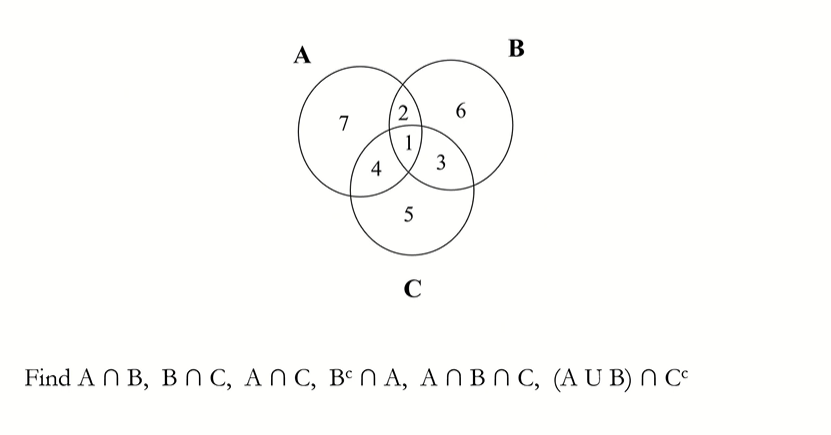
Set Operations - Intersection (교집합)

A : 첫 번째 Event
B : 두 번째 Event

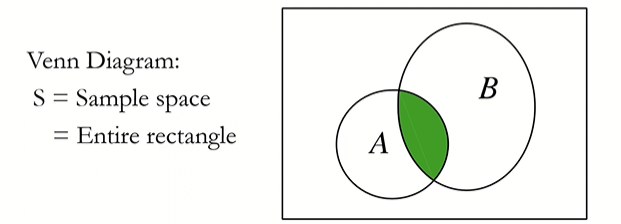
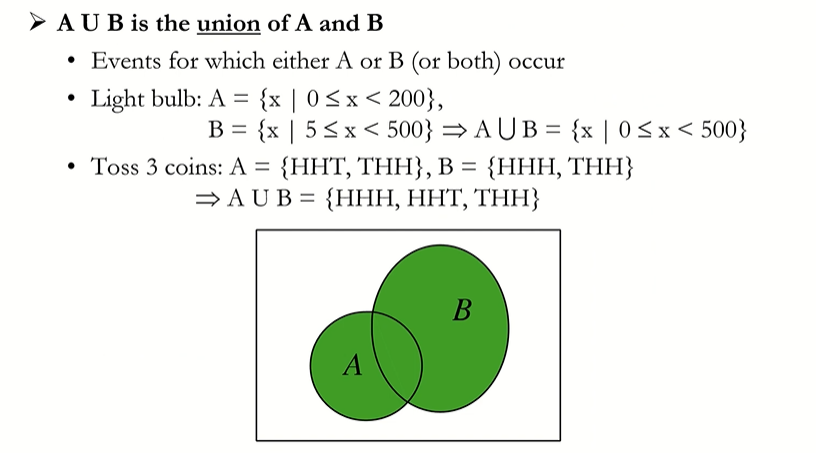
Set Operations - Union (합집합)

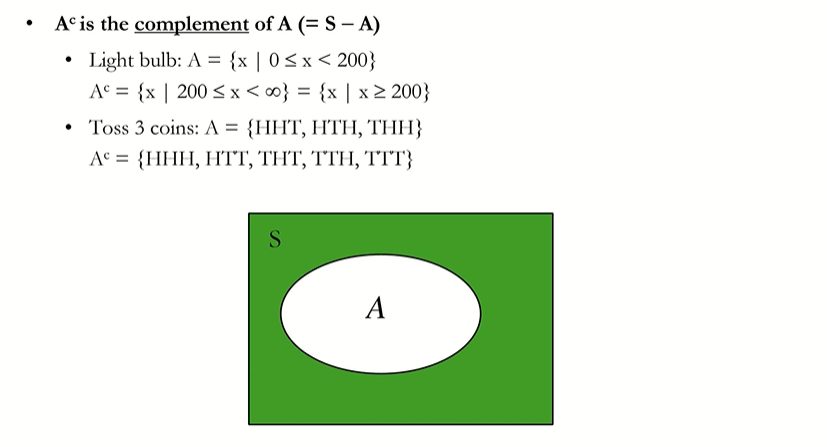
Set Operations - Complement (여집합)

Laws of Set Operations

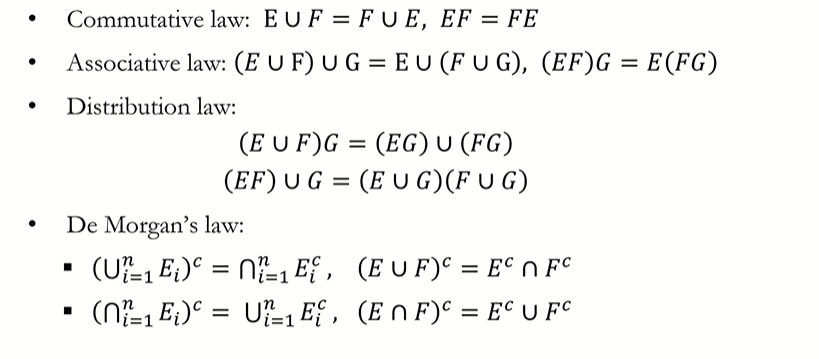
Commutative law : 교환 법칙
Associative law : 결합 법칙
De Morgan's law : 드모르간 법칙

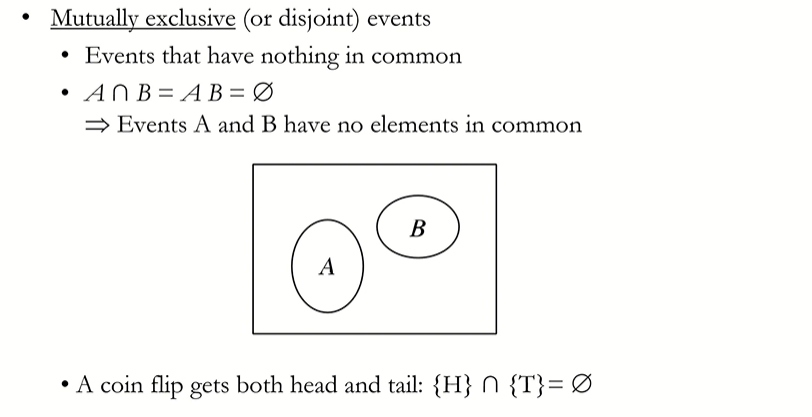
Set Operations - Mutually Exculsive (상호배타)

Venn Diagrams - Example

Axioms of Probability

P(S) = 모든 Sample State에 대한 Probability
Sample States 안에 있는 모든 이벤트들이 상호 배타 관계라면, 모든 이벤트들의 합집합애 대한 확률 = 각 이벤트들의 합

상호배타적인 관계를 가지고 있는 이벤트들이 있는데, 적어도 하나의 이벤트가 일어날 확률은 모든 이벤트들의 합

Probability Example

S = Sample State

Probability of an Example

Basic Properties of Probability

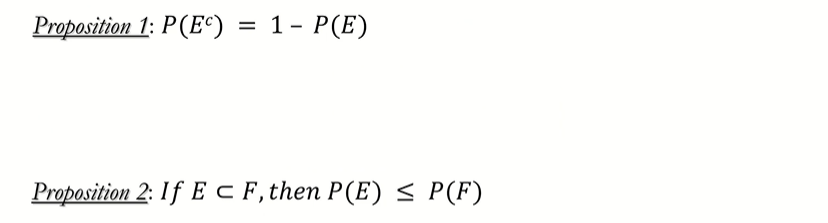
Example of Proposition

Extension of Proposition

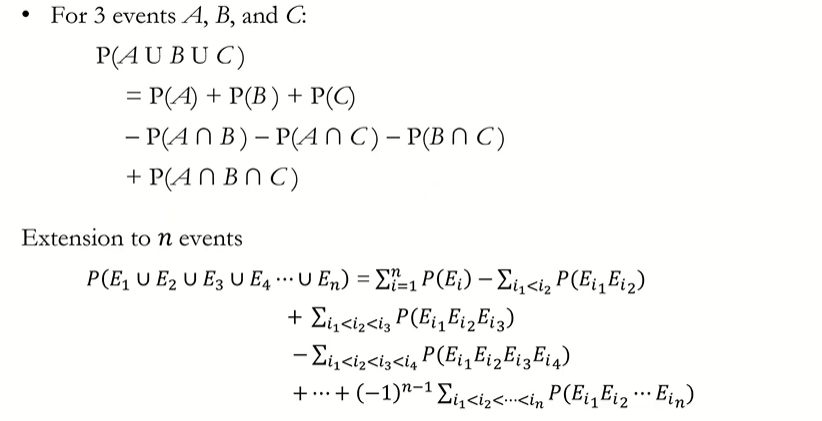
Example of Proposition 3

We conclude that 43 members play at least one of the sports

Equally Likely Outcomes

Outcomes : 동일확률

Equally Likely Outcomes - Example

S = 36가지

Example - Birthday Problem

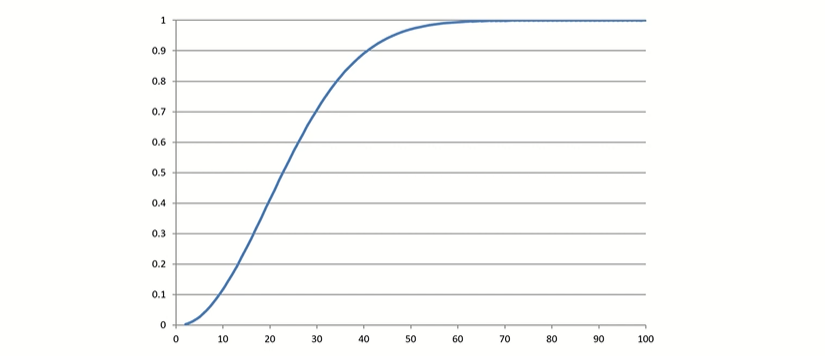
When there are 23 people in the room, the probability that at least two shares the same birthday is 0.507
When there are 57 people in the room, the probability that at least two shares the same birthday is 0.99

Example - The Matching Problem

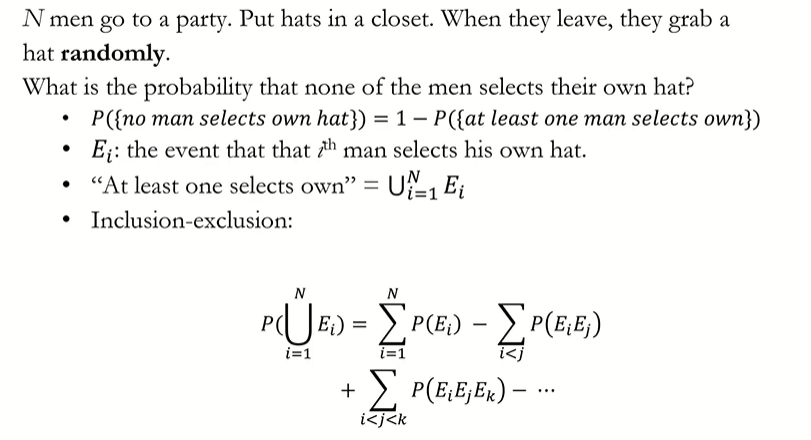
Example - The Matching Problem (Con't)

[핵심 확률/통계] Axoims of Probability 강의자료