Conditional Probability and Independence -1

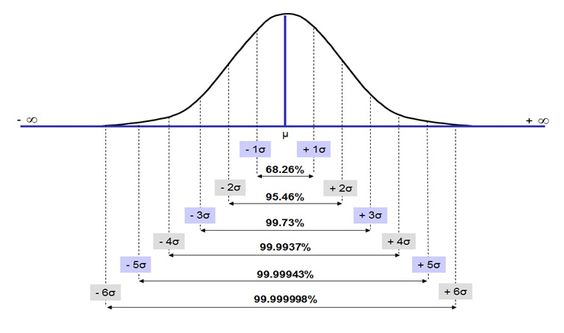
Conditional Probability (조건부확률)

P(EF) = P(E)와 P(F)의 교집합

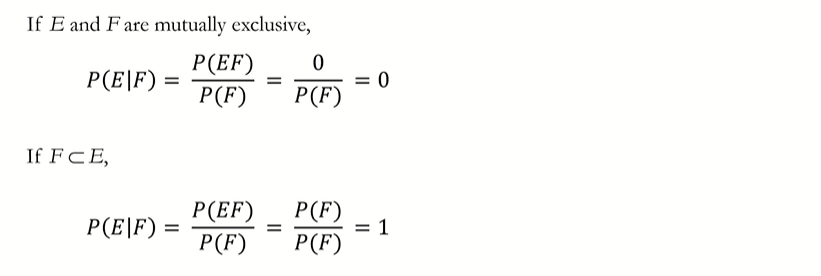
Conditional Probability - Example

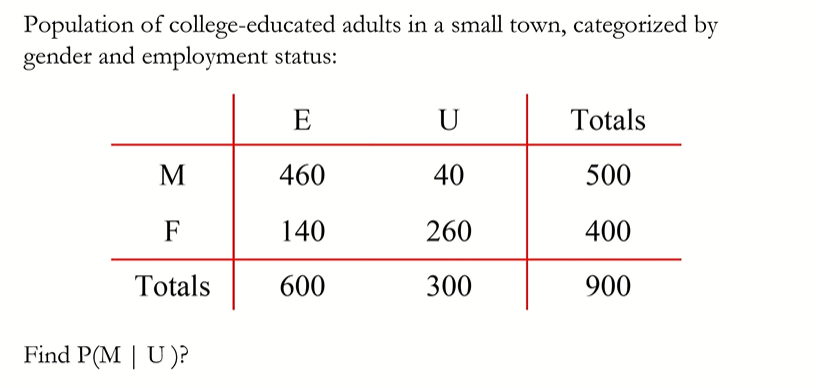
P(M|U) = P(MU)/P(U)
P(U) = 300/900
P(MU) = 40/900
P(M|U) = 40/300 = 2/15

P(S|R) = P(SR)/P(R)
P(U) = 36/150
P(MU) = 96/150
P(M|U) = 3/8
P(D|R) = 1 - P(S|R) = 5/8

B : Both heads : {(h,h)}
F: First heads : {(h,h), (h,t)}
A : at least on head : {(h,h), (h,t), (t,h)}

P(FA) = P(F) X P(A|F)
= 1/2 X 1/2 = 1/4

Multiplicative Rules in Probability

P(A|B) = P(AB)/P(B)
P(B|A) = P(AB)/P(A)

Baye's Rule(베이즈 룰)

Law of Total Probability(전확률 법칙)

A1, A2, A3 -> mutually exculsive

P(A1 | B) (정보) P(A1) *

Bayes's Rule - Supplier Example

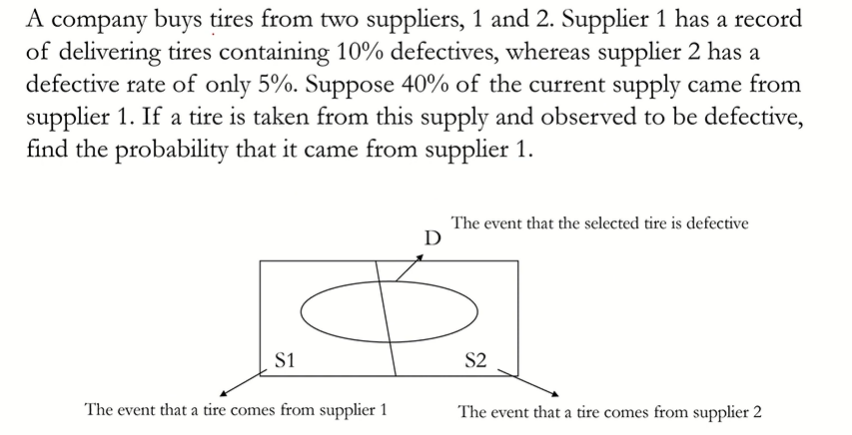
Baye's - Supplier Example (Con't)

P(S1) = 0.4, P(S2) = 0.6
P(D|S1) = 0.1, P(D|S2) = 0.05
P(S1|D) = P(S1D)/P(D)
= P(S1D)/{P(S1D) + P(S2D)}
= P(S1) X P(D|S1) / {P(S1) X P(D|S1) + P(S2) X P(D|S2)}
= 0.4 X 0.1 / 0.4 X 0.1 + 0.6 X 0.05
= 0.57

Baye's Rule - Teaching Methods

What is the probability that he was taught by Method A

P(A) = 0.7 P(B) = 0.3
P(F|A) = 0.2, P(F|B) = 0.1
P(A|F) = P(AF) / P(F)
= P(AF) / P(AF) + P(BF)
= p(A) X P(F|A) / P(A) X P(F|A) + P(B) X P(F|B)
= 0.7 X 0.2 / 0.7 X 0.2 + 0.3 X 0.1
= 0.82

Baye's Rule - Criminal Investigation

criminal investigation = 범행조사
P(G) = 0.6, P(~G) = 0.4
P(C|G) = 1 P(C|~G) = 0.2
P(G|C) = p(GC) / P(C)
= P(C|G) XP(G) = P(C|G) X P(G) + P(C|~G)P(~G)
= 0.882

Baye's Rule - Disease Example

Odds (아즈, 오즈)

Odds - Coins in Urn Problem

Hence, the odds are 2/3, or, equivalently, the probability is 2/5 that a type A coin was flipped

urn = 항아리
P(A|H) = P(A) X P(H|A) / P(H)
P(B|H) = P(B) X P(H|B) / P(H)
P(A|H) / P(B|H)
P(A) = 2/3
P(B) = 1/3
P(H|A) = 1/4
P(H|B) = 3/4
P(A|H) / 1- P(A|H) -> P(A|H) = 2/5

[핵심 확률/통계] = 조건부 확률(Conditional Probability) 강의 자료 슬라이드 참조