B-Tree 소개와 특징

B-Tree는 효율적인 탐색을 위해 탄생한 자료구조입니다. 기존의 이진 탐색 트리에서는 한 노드 당 최대 두 개의 자식을 가질 수 있었던 반면 B-Tree는 한 노드가 다수의 자식 노드를 가질 수 있다라는 특징이 있습니다.

또한 B-Tree는 모든 리프 노드(최하위 노드)가 동일한 레벨을 가진다는 특징도 가지고 있습니다.

B-Tree는 주로 MySQL과 같은 RDBMS에서 효율적으로 데이터를 탐색하기 위해 사용됩니다.

---

B-Tree 구조

노드 구성

B-Tree에서 노드는 키 Key와 포인터 Pointer로 구성됩니다.

먼저 키는 노드에 저장된 값들의 배열로 반드시 오름차순으로 정렬되어 저장됩니다.

포인터는 키 값 보다 작거나 큰 서브 트리를 가리킵니다.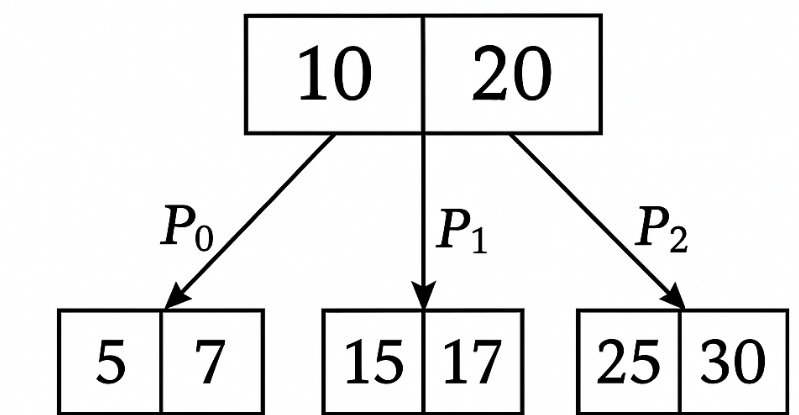
위 이미지에서 포인터 P0는 10보다 작은 서브 트리를 가리키고, P1은 10보다 크고 20보다 작은 서브 트리를 P2는 는 20보다 큰 서브 트리를 가리키게 됩니다.

B-Tree의 최대 키 수는 차수 m(order m)일때 최대 m - 1개의 키를 가질 수 있습니다. 키의 앞뒤에 포인터가 위치하므로 최소 키 수는 m/2 - 1 개를 갖습니다.
예외적으로 루트 노드에서만 1개 이상의 키를 갖도록 허용하고 있습니다.

노드 종류

B-Tree는 루트 노드, 내부 노드, 리프 노드로 구성됩니다.

루트 노드는 최상위 노드로 자식이 존재하는 경우 최소 키가 한 개 이상 존재합니다.

내부 노드(Internal Node)는 서브 트리를 갖는 노드로 분기점역할이 되는 노드입니다. 데이터 탐색 과정에서 어떤 서브 트리로 진행해야하는지에 대한 결정을 하게 만들어줍니다.

리프 노드는 실제 데이터를 보관하는 노드들입니다. B-Tree에서 리프 노드들은 동일한 레벨에 위치함을 보장합니다.

---

B-Tree 동작

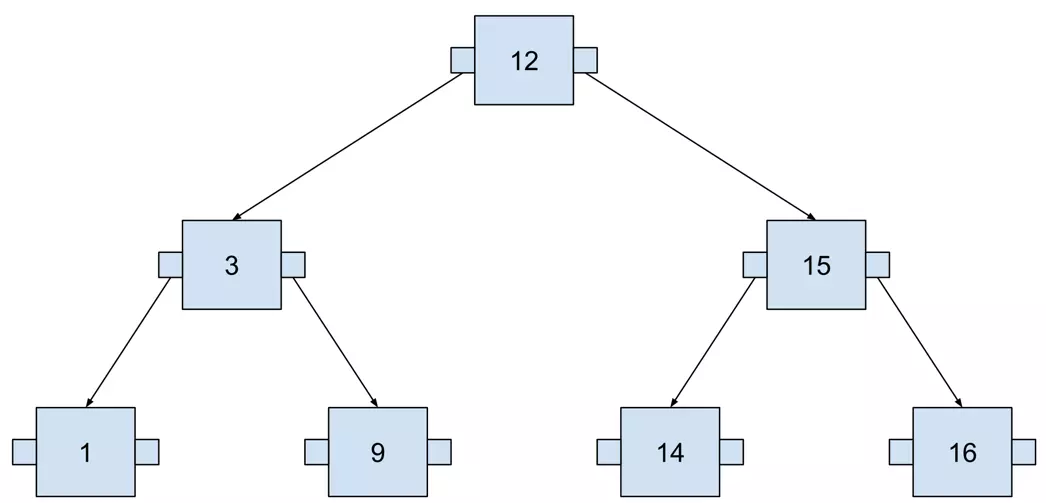
트리 이미지 출처
https://blog.allegro.tech/2023/11/how-does-btree-make-your-queries-fast.html

검색

B-Tree의 검색은 다음과 같이 이루어집니다.

1. 루트 노드에서 하향식으로 검색
2. 각 노드의 키들을 하나씩 검사
3. 검색 대상을 키에서 찾았다면 반환하고 검색 종료
4. 그렇지 않다면 검색 대상과 키를 비교 후 대소관계에 따라 서브 트리로 이동하여 2-3 or 2-4 과정을 반복

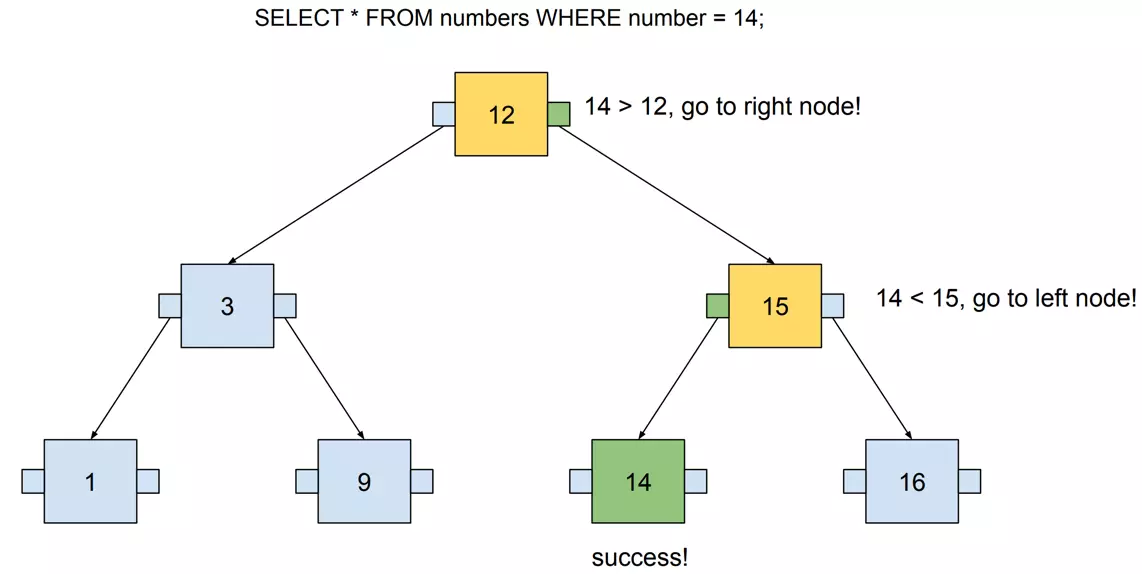
14 탐색 과정에서 루트 노드의 키가 12이므로 더 큰 오른쪽 서브 트리로 이동.
서브 트리의 키가 15로 14보다 크므로 더 작은 수들을 저장해놓은 왼쪽 서브 트리로 이동 후 14 탐색 성공.

B-Tree의 탐색은 이진 탐색 트리의 탐색 과정과 비슷한 원리를 사용하고 있습니다.

삽입

탐색은 이진 탐색의 원리를 이용해서 딱히 어려운게 없었는데요. 문제는 삽입과 삭제입니다. 리프 노드들을 반드시 같은 레벨에 유지시켜야하기 떄문에 동적으로 분할 & 병합을 이용해서 삽입과 삭제를 수행하여 리프 노드의 레벨이 동일하게 유지되도록 합니다.

먼저 삽입은 다음과 같이 이루어집니다.

삽입하고자 하는 키 값이 k일 때

1. 검색 연산을 통해 k를 삽입하기 적당한 리프 노드를 탐색
2. 검색된 적절한 위치의 리프 노드의 키 배열에 k를 삽입
3. 오버플로우 검사를 수행 (최대 키 수인 m - 1을 넘으면 오버플로우)
4. 오버플로우가 발생했다면 분할을 수행. 발생하지 않았다면 키 삽입

노드 분할

노드의 최대 키 수가 m - 1개 이므로 삽입 과정에서 키 수가 m - 1보다 커지면 오버플로우가 발생합니다. 그리고 이에 따라 노드 분할을 수행하게 됩니다.

노드 분할은 다음과 같은 과정으로 수행됩니다.

1. 키 배열에서 중앙 값(키)를 선택
2. 중앙 키보다 작은 값은 왼쪽의 새 노드, 큰 값은 오른쪽의 새 노드로 분할
3. 중앙 값을 부모 노드의 키 배열로 삽입
4. 이 과정에서 부모 노드도 오버플로우가 발생하면 재귀적으로 노드 분할을 수행

만약 키 승격 과정에서 분할 해야하는 대상이 루트 노드가 된다면 새 루트 노드를 만들고 승격 키를 루트 노드의 유일한 키로 넣습니다. (트리 차수 1 증가)

삭제

다음으로 삭제는 다음과 같이 이루어집니다.

1. 검색 연산을 통해 k가 저장된 노드를 탐색
2. 찾은 노드에서 키 삭제
3. 언더플로우 검사 수행 (최소 키 수인 m/2 - 1개 보다 적으면 언더플로우)
4. 언더플로우가 발생했다면 재분배 or 병합을 수행하여 리프 노드의 레벨을 유지

리프 노드 키 삭제

리프 노드에서 키 삭제가 이루어지는 경우 키 삭제 후 언더플로우 검사를 수행합니다. 그 후 언더플로우 발생 여부에 따라 노드 재분배 or 병합을 수행하게 됩니다.

내부 노드 키 삭제

내부 노드에서 삭제가 일어나는 경우에는 리프 노드 삭제보다 조금 더 복잡한 삭제 과정을 거칩니다.

1. 삭제 대상 k의 전임, 후임 중 하나를 대체키로 선택
   • 전임: 왼쪽 자식 서브 트리(작은 값 트리)에서 가장 큰 키
   • 후임: 오른쪽 자식 서브 트리(큰 값 트리)에서 가장 작은 키
2. 1에서 선택한 대체키를 내부 노드의 k와 교체
3. 이후 언더플로우 검사 후 재분배 or 병합 수행

내부 노드의 경우 실제로는 대체키를 삭제하고 원래 k는 대체키로 바꾸는 연산을 수행합니다.

노드 재분배, 노드 병합

언더플로우가 발생한 경우 노드 재분해 or 노드 병합을 이용해서 리프 노드들의 레벨을 동일하게 맞춰줍니다.

언더플로우가 발생한 노드를 x, x의 형제 노드(같은 부모 노드 p를 갖는 옆 트리)를 s라고 칭합니다.

먼저 노드 재분배 Redistribution은 다음과 같은 방식으로 수행됩니다.

노드 재분배는 s의 키 개수가 m/2보다 같거나 큰 경우 수행합니다.

1. p에서 경계키(x와 s를 구분하는 부모 p의 키)를 하나 가져와 x에 삽입
2. s에서 가장 가까운 키(경계키와 가장 가까운 키)를 p로 올림
3. 포인터도 함께 올림

다음으로 노드 병합 Merge는 다음과 같은 방식으로 수행됩니다.
1. p에서 경계키를 하나 가져와 x, s와 하나의 노드로 병합
2. p도 키-포인터 쌍이 삭제되어 언더플로우가능성이 생기므로 재귀적으로 언더플로우 검사 수행 후 필요하다면 노드 재분배와 병합 수행

만약 삭제 과정에서 루트 노드의 키가 0이 되면 루트 노드의 유일한 자식 노드를 루트로 만들어서 트리의 균형을 유지합니다. (트리 차수 1 감소)