
리스트와 스택, 큐는 1:1 구조의 자료구조, 트리는 1:다의 자료구조였습니다. 그렇다면 다:다 관계를 가진 자료구조도 존재할 것 같다는 생각이 듭니다. 그래프는 이처럼 다:다의 관계를 가진 자료구조 입니다.
그래프 Graph
 지하철 노선도 처럼 한 역에서 찍어서 다른 역에 도달하는 방법까지는 수많은 방법이 있습니다. 그리고 한 역은 하나의 역만 연결될 수도 있고 수많은 역과 연결되어 있을 수도 있습니다. 이런 지하철 노선도가
지하철 노선도 처럼 한 역에서 찍어서 다른 역에 도달하는 방법까지는 수많은 방법이 있습니다. 그리고 한 역은 하나의 역만 연결될 수도 있고 수많은 역과 연결되어 있을 수도 있습니다. 이런 지하철 노선도가 그래프를 가장 잘 나타내주고 있습니다.
그래프(Graph)는 다:다의 관계를 가진 정점과 간선으로 이루어진 자료구조입니다. 정점은 객체(Vertex)를 나타내고 간선(Edge)은 객체끼리의 연결을 의미합니다. 이때 그래프 G는 G=(V, E)와 같은 형태로 정의합니다.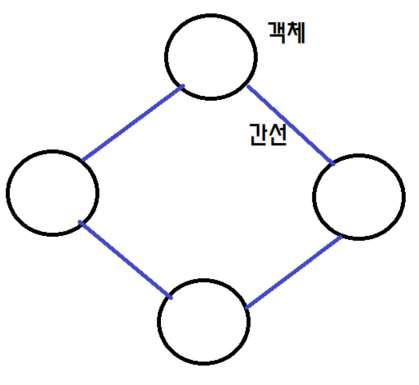
그래프의 종류
그래프는 얼마나 연결되었는가 혹은 방향성이 존재하는가에 따라서 몇 가지의 분류를 할 수 있습니다.
무방향 그래프
무방향 그래프는 방향성이 없는 그래프를 의미합니다.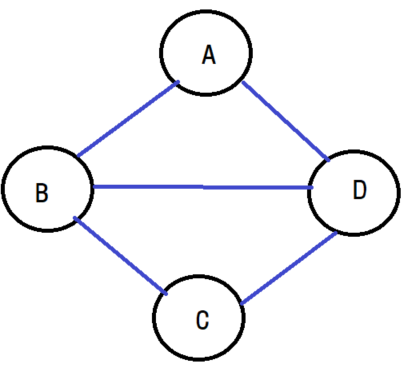
방향 그래프
방향 그래프는 간선에 방향이 존재하는 그래프입니다. 방향 그래프는 다른말로 다이그래프(Digraph)라고도 합니다. 방향 그래프에서 간선의 화살표 시작 부분을 꼬리(tail)이라고 하고, 뾰족한 부분인 끝 부분은 머리(head)라고 합니다.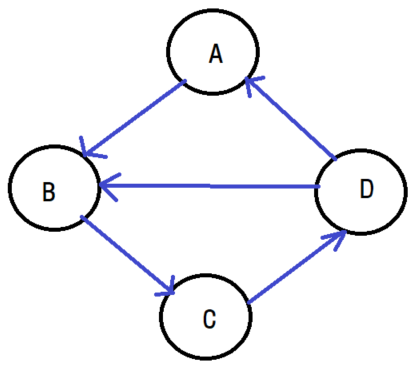
완전 그래프
완전 그래프는 각 정점들 사이에서 연결 가능한 모든 정점들을 연결하여 최대의 간선수를 가진 그래프입니다.
같은 정점의 갯수를 가진 완전 그래프라도 무방향/방향 그래프냐에 따라서 간선의 수가 차이나게 됩니다. 무방향 그래프라면 최대 간선의 수는 정점 n개에 대해서 n(n-1)/2개, 방향 그래프라면 n(n-1)개가 됩니다.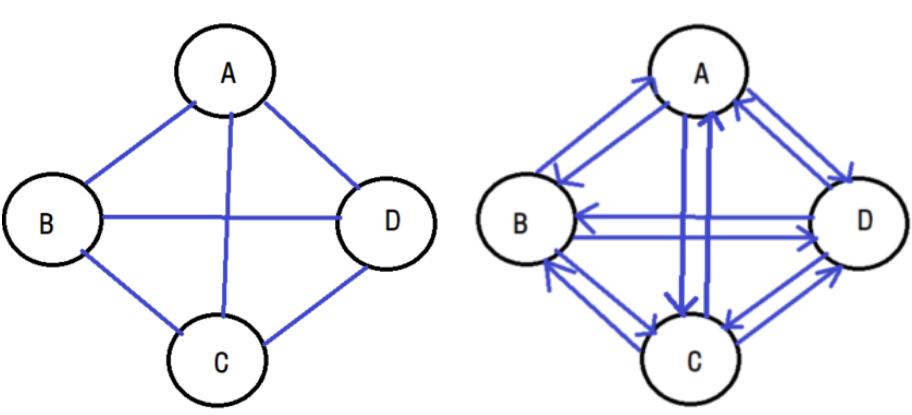
부분 그래프
부분 그래프는 원래 그래프에서 간선이나 정점이 몇개 제외된 그래프들을 의미합니다. 즉 이진 트리의 서브 트리처럼 그래프 내의 작은 그래프라고 할 수 있습니다.
다음과 같은 그래프 G가 있습니다.
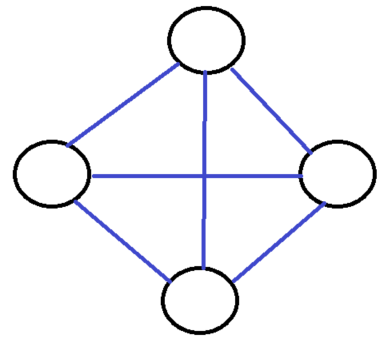 이 그래프는 아래와 같은 여러가지 부분 그래프를 가질 수 있습니다.
이 그래프는 아래와 같은 여러가지 부분 그래프를 가질 수 있습니다.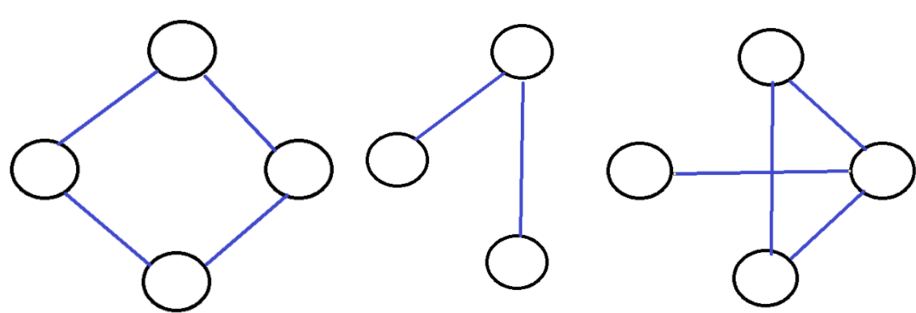
가중치 그래프
가중치 그래프는 간선에 가중치를 부여한 그래프입니다. 네트워크(Network)라고도 합니다. 가중치는 정점 사이를 이동하는데 소모되는 자원이나 시간의 양으로 계산되어 최단 거리 찾기 등에 이용됩니다.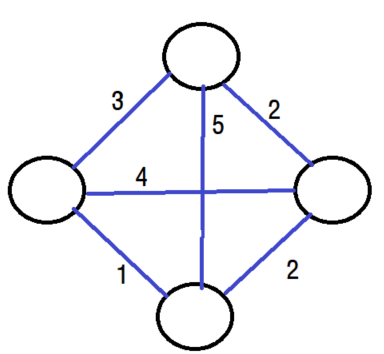
그래프 표현
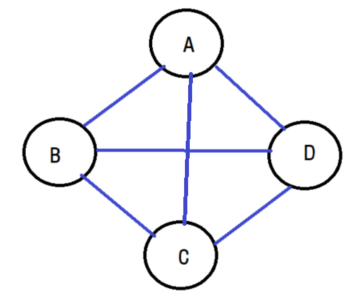 위와 같은 그래프 G가 있을 때 정점과 간선의 집합은 다음과 같이 표시합니다.
위와 같은 그래프 G가 있을 때 정점과 간선의 집합은 다음과 같이 표시합니다.
V(G) = { A, B, C, D }
E(G) = { (A, B), (A, C), (A, D), (B, C), (B, D), (C, D) }
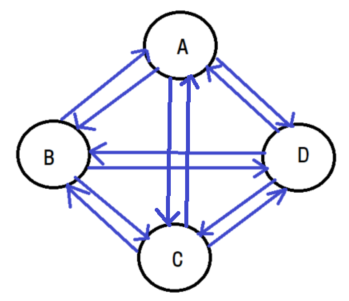 만약 방향 그래프라면 간선의 표현은 다음과 같습니다.
만약 방향 그래프라면 간선의 표현은 다음과 같습니다.
E(G) = {
<A, B>, <A, C>, <A, D>, <B, A>, <B, C>, <B, D>,
<C, A>, <C, B>, <C, D>, <D, A>, <D, B>, <D, C>
}
