모든 자료구조가 그래왔듯이 그래프를 구현하는 방식에는 순차 자료구조를 이용하는 방식과 연결 자료구조를 이용하는 방식 두가지가 있습니다. 그래프에서도 마찬가지이지만 이름을 조금 다르게 부릅니다.

순차 자료구조를 이용해서 구현하는 것을 인접 행렬 기반 그래프, 연결 자료구조를 이용해서 구현하는 것을 인접 리스트 기반 그래프 라고합니다. 오늘은 첫 번째 순차 자료구조를 이용한 방식인 인접 행렬을 이용한 그래프를 구현해보겠습니다.

인접 행렬 Adjacent Matrix

인접 행렬은 그래프에서 정점이 어떤 간선으로 연결되었는지를 나타내는 행렬입니다. 정점 n개의 그래프에 대해서 n X n행렬을 이용합니다. 이때 정점끼리 연결되어 있다면 행렬의 값을 1로, 연결되어있지 않다면 행렬의 값을 0으로 이용합니다.

예시로 그래프에 대해서 행렬을 나타내보겠습니다.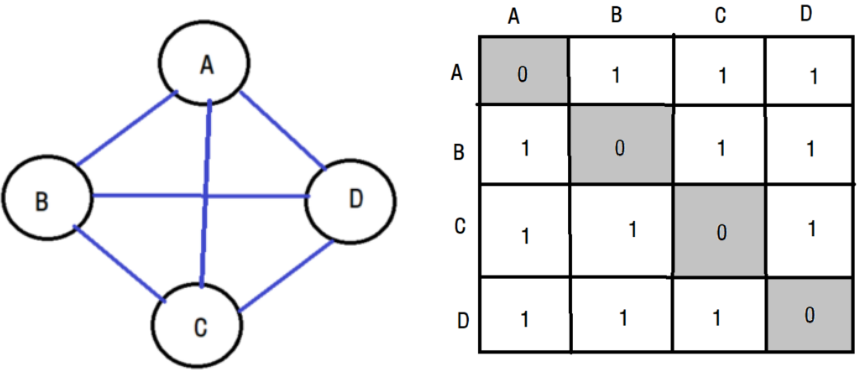

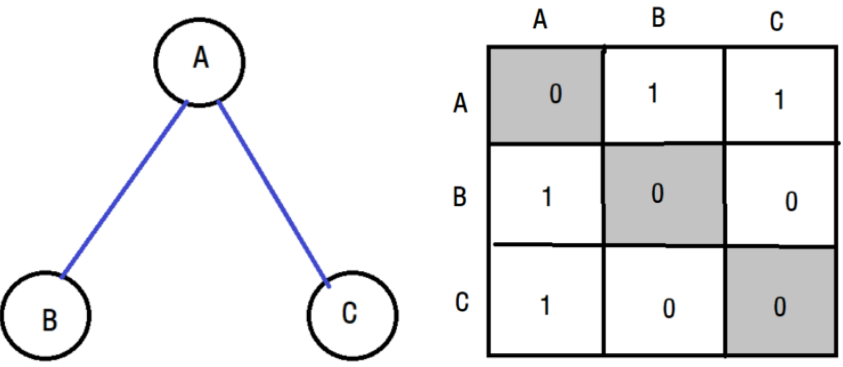
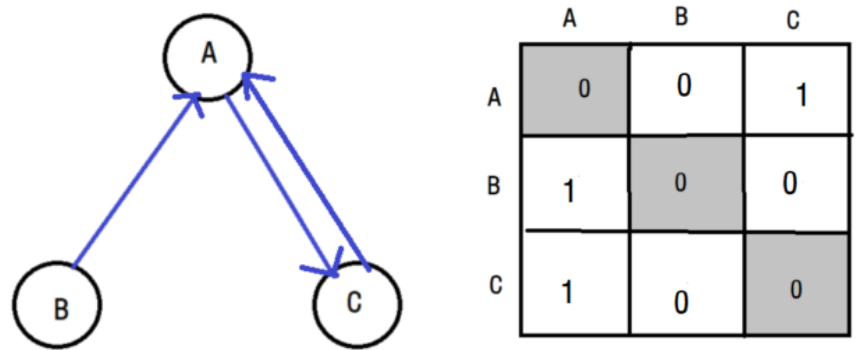
인접 행렬 그래프 구현

행렬 표현을 이해했다면 인접 행렬 그래프를 구현해볼 차례입니다. n X n 행렬을 이용하기 때문에 배열중에서도 2차원 배열을 이용해야겠다는 것이 감이 오나요?

구조 정의

그래프의 기본 구조입니다. 크기는 널널하게 10x10의 2차원 배열을 선언했습니다.

#define MAX_VERTEX 10

typedef struct graph {
	int n;	//n은 그래프의 정점(node)의 갯수
	int adjacentMatrix[MAX_VERTEX][MAX_VERTEX];	//nXn 행렬을 위한 2차원 배열
}graph;

정점 삽입

정점 삽입은 간단합니다. 최대 정점수를 넘지 않는다는 조건하에서 조건을 만족하면 정점 수를 +1 하기만 하면 됩니다.

void insertVertex(graph* g, int v) {
	if (g->n + 1 > MAX_VERTEX) {	//최대 정점 수 보다 정점수가 많아진다면 삽입 취소
		return;
	}

	g->n++;
}

정점 삽입이 이렇게 간단한 이유는 인접 행렬에 이유가 있습니다. 인접 행렬에는 간선이 연결 되었는지의 정보만을 담습니다. 그렇기 때문에 다른 추가적인 작업이 필요가 없는 것이죠.

간선 삽입

void insertEdge(graph* g, int tail, int head) {
	if ((tail >= g->n) || (head >= g->n)) {	//간선을 이을 수 없다면 간선 삽입 취소
		return;
	}

//간선을 삽입하고 둘 사이가 연결되었음을 인접 행렬에 알린다.
	g->adjacentMatrix[tail][head] = 1;
}

---

인접 행렬 그래프의 전체 코드는 GitHub에서 확인하실 수 있습니다.