힙(Heap) 혹은 히프는 완전 이진 트리 종류 중 하나 입니다. 힙는 여태까지 트리를 계속 해서 연결 자료구조로 구현한 것과는 다르게 1차원 배열을 이용해서 구현할 수 있는 자료구조 이기도 합니다.

힙 Heap

힙(Heap)은 이진 트리의 노드들 중에서 키값이 가장 큰 값또는 가장 작은 값을 찾기 위한 자료구조입니다. 이때 가장 큰 값을 찾으면 최대 힙, 가장 작은 값을 찾으면 최소 힙이라고 합니다. 또 다른 특징은 힙은 같은 키값을 가진 노드를 가질 수 없다는 점 입니다. 그래서 최대 힙에서는 가장 큰 키값을 가진 노드가 루트 노드가 되고, 최소 힙에서는 가장 작은 키값을 가진 노드가 루트 노드가 됩니다.

힙은 1차원 배열로 구현하기 때문에 배열의 인덱스를 통해 트리간의 부모 자식관계를 쉽게 알 수 있다는 점도 있습니다.

또한 힙이라고 그냥 부르게 되면 최대 힙을 의미하게 됩니다. 그래서 잠시후에 할 구현도 최대 힙을 구현하려고 합니다.

힙 구현하기

힙은 1차원 배열로 구현합니다. 전에 배운 이진 트리의 배열 구현처럼 인덱스 0는 비워두고 1부터 이용하는데 이때 배열의 인덱스 번호가 노드의 번호이고 인덱스에 저장된 값이 노드의 키값이 됩니다.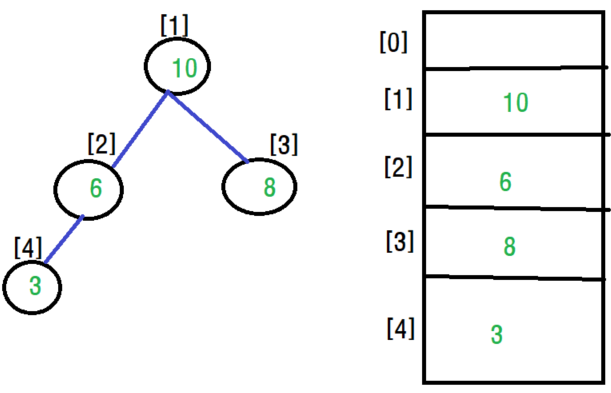

기본적인 힙 구조는 다음과 같습니다.

#define MAX 20

typedef struct {
	int heap[MAX];	//힙 구조인 1차원 배열, 인덱스는 최대 MAX개 까지
	int heapSize;	//현재 힙 크기
}heapType;

데이터 삽입

힙에 데이터를 삽입하기 전에 명심해야 할 것은 힙은 완전 이진 트리의 한 종류라는 것 입니다. 그래서 마지막 노드 다음에 새 노드가 들어갈 자리를 만들고, 삽입을 진행해야합니다. 이때 삽입 과정에서도 부모 노드보다 삽입 노드의 키값이 크다면 위치를 바꿔주는 작업도 해야합니다.

void insertHeap(heapType* h, int elem) {
	h->heapSize = h->heapSize + 1;	//우선 힙의 크기를 1 늘려줍니다.

	int i = h->heapSize;
	
    //삽입 위치 조정. 부모 노드의 키값과 비교해서 
	while ((i != 1) && (elem > h->heap[i / 2])) {
		h->heap[i] = h->heap[i / 2];
		i /= 2;
	}

	h->heap[i] = elem;
}

이 과정에서 While 반복문이 삽입 위치를 조정합니다.

while ((i != 1) && (elem > h->heap[i / 2])) { ... }

elem(삽입할 노드 키값)이 현재 삽입 위치의 부모 노드 키값보다 크다면 위치를 재조정해서 다시 삽입을 시도합니다.

데이터 삭제

힙에서 데이터를 삭제하는 연산의 큰 특징은 항상 루트 노드의 키를 삭제한다는 것입니다. 즉, 최대 힙이라면 가장 큰 값을, 최소 힙이라면 가장 작은 값을 삭제하는 연산이 됩니다. 삽입과 마찬가지로 삭제 연산 이후에도 반드시 완전 이진 트리의 형태를 가지고 있어야 한다는 점입니다.

삭제는 항상 루트 노드를 삭제합니다. 이 루트 노드는 인덱스 1번 입니다. 하지만 힙 사이즈도 -1 하게되면 인덱스 1이 사라지는 것이 아니라 인덱스 n-1이 사라지게되죠.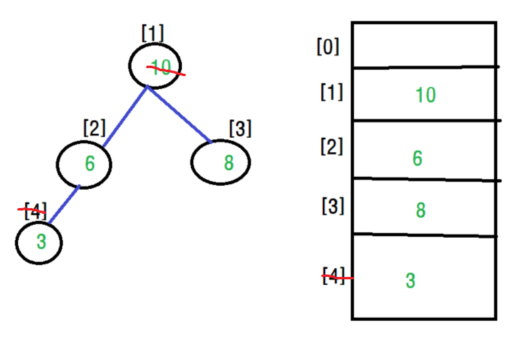그래서 삭제연산은 인덱스가 사라진 저 [4]번의 요소인 3을 [1]번 인덱스에 넣은 다음 올바른 자리로 찾아가는 방식을 이용합니다.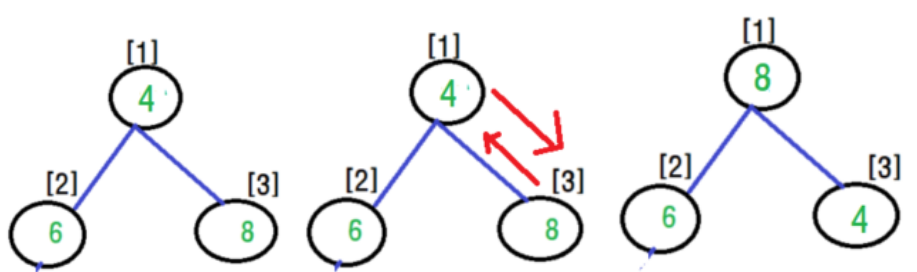

void deleteHeap(heapType* h) {
	int parent, child, temp;
	
    //임시변수 temp에 인덱스의 제일 마지막 키값을 넣어둡니다. 
	temp = h->heap[h->heapSize];
    //힙 사이즈를 1줄입니다.
	h->heapSize = h->heapSize - 1;

	parent = 1;
	child = 2;

	//임시로 1번 인덱스에 저장해둔 temp의 위치를 찾기 위한 반복문
	while (child <= h->heapSize) {
    //h->heap[child]는 왼쪽 자식 노드, [child+1]은 오른쪽 자식 노드
		if ((child < h->heapSize) && (h->heap[child] < h->heap[child + 1])) {
			child++;
		}
        
        //위 if문에서 찾은 자식 노드보다 temp가 같거나 크면 위치를 찾았기에 break
		if (temp >= h->heap[child]) {
			break;
		}
        //찾은 자식 노드보다 temp가 작으면
		else {
        //자식 노드와 부모 노드의 위치를 바꾸고 위치를 계속 찾아나갑니다.
			h->heap[parent] = h->heap[child];
			parent = child;
			child *= 2;
		}
	}
    
    //찾아낸 위치에 temp의 값을 삽입해 완전 이진 트리 형태로 만든다
	h->heap[parent] = temp;
}

---

전체 코드는 GitHub에서 확인하실 수 있습니다.