지난 포스트에서 이진 트리를 구현해 보면서, 트리 삽입 과정에서 문제가 발생했었습니다. 트리의 하위 트리가 존재하는 경우 그 아래 트리의 메모리가 반환되지 않아 메모리 낭비가 일어나는 과정이었는데요. 이 과정을 순회 라는 개념으로 해결할 수 있다고 했었습니다.

순회

순회는 트리의 모든 노드를 중복이나 빠지는 것 없이 처리하는 연산입니다. 그동안 우리가 다뤘던 스택, 큐같은 자료구조들을 자료가 1:1 구성을 가졌기에 따로 순회할 필요가 없었습니다. 그러나 트리는 1:다수의 관계이기 때문에 현재 노드에서 어떤 다음 노드를 처리할지에 대한 연산이 필요하며, 이 연산을 순회라고 합니다.

순회는 루트 노드의 방문 순서를 기준으로 세 가지 종류로 나뉩니다.

• 전위 순회
• 중위 순회
• 후위 순회

전위 순회는 루트 노드에서 순회를 시작합니다.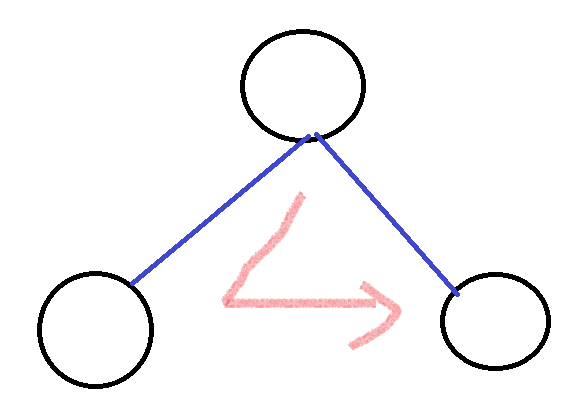중위 순회는 루트 노드를 중간에 방문하게 됩니다.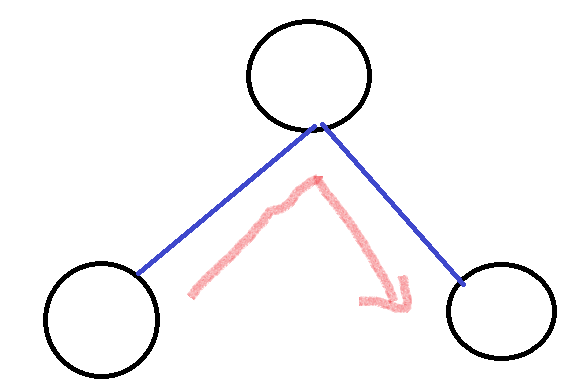후위 순회는 루트 노드의 방문이 제일 마지막인 순회입니다.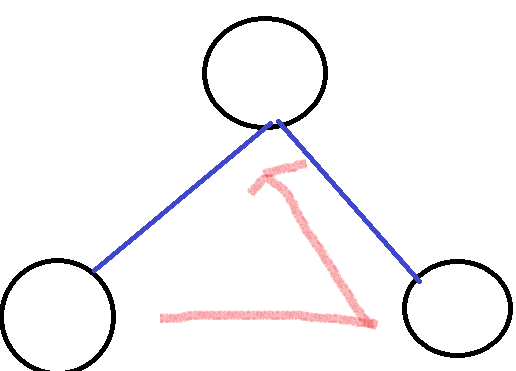

---

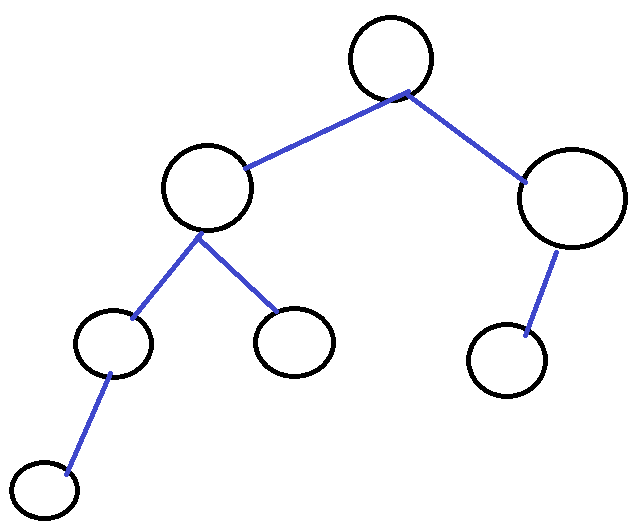이진 트리는 각 노드마다 새로운 서브 트리를 만들 수 있다고 했습니다. 그래서 위 그림처럼 높이가 2이상인 트리는 트리들을 분해해서 서브 트리를 만들고 각 서브 트리에 대하여 재귀 함수를 이용해서 순회를 반복합니다.

순회 구현하기

순회 구현의 원리는 위에서 이야기했었는데요. 트리를 분해해서 루트 노드, 자식 노드로 이루어진 서브트리에서 각각 순회를 한다고 생각하면 생각보다 간단하게 구현이 됩니다. 만약 분해한 서브 트리에 자식 노드가 존재해서 또 다른 서브 트리가 만들어진다면 재귀를 통해 그 서브 트리에 대한 순회 연산을 실행하면 됩니다.

void preorder(binaryTreeNode* BT) {
	if (BT) {
		//현재 노드 연산 위치(전위 순회)
		preorder(BT->leftNode);
		preorder(BT->rightNode);
	}
}

void inorder(binaryTreeNode* BT) {
	if (BT) {
		inorder(BT->leftNode);
		//현재 노드 연산 위치(중위 순회)
		inorder(BT->rightNode);
	}
}

void postorder(binaryTreeNode* BT) {
	if (BT) {
		postorder(BT->leftNode);
		postorder(BT->rightNode);
		//현재 노드 연산 위치(후위 순회)
	}
}

---

순회도 구현했으니 지난번에 구현한 이진 트리와 합치면, 최종적으로 완성된 이진 트리가 구현됩니다.

#include <stdio.h>
#include <stdlib.h>

typedef int element;

typedef struct BinaryTreeNode {
	struct BinaryTreeNode* leftNode;
	element data;
	struct BinaryTreeNode* rightNode;
}binaryTreeNode;

binaryTreeNode* createBinaryTree(void) {
	binaryTreeNode* BT;

	BT = (binaryTreeNode*)malloc(sizeof(binaryTreeNode));
	BT->leftNode = NULL;
	BT->rightNode = NULL;

	return BT;
}

void makeLeftSubTree(binaryTreeNode* current, binaryTreeNode* sub) {
	if (current->leftNode != NULL) {
		free(current->leftNode);
	}

	current->leftNode = sub;
}

void makeRightSubTree(binaryTreeNode* current, binaryTreeNode* sub) {
	if (current->rightNode != NULL) {
		free(current->rightNode);
	}

	current->rightNode = sub;
}

void setData(binaryTreeNode* BT, element elem) {
	BT->data = elem;
}

element getData(binaryTreeNode* BT) {
	return BT->data;
}

binaryTreeNode* getLeftSubTree(binaryTreeNode* BT) {
	return BT->leftNode;
}

binaryTreeNode* getRightSubTree(binaryTreeNode* BT) {
	return BT->rightNode;
}

void preorder(binaryTreeNode* BT) {
	if (BT) {
		//현재 노드 연산 위치(전위 순회)
		preorder(BT->leftNode);
		preorder(BT->rightNode);
	}
}

void inorder(binaryTreeNode* BT) {
	if (BT) {
		inorder(BT->leftNode);
		//현재 노드 연산 위치(중위 순회)
		inorder(BT->rightNode);
	}
}

void postorder(binaryTreeNode* BT) {
	if (BT) {
		postorder(BT->leftNode);
		postorder(BT->rightNode);
		//현재 노드 연산 위치(후위 순회)
	}
}

전체 코드는 GitHub에서도 확인하실 수 있습니다.