AVL 트리

Bam·2022년 3월 6일

Data Structure

목록 보기

16/22

이진 탐색 트리는 트리 구조마다 연산시간이 천차만별입니다. 다음 그림처럼 같은 노드를 가져도 구조에 따라서 연산시간이 다르게 됩니다. 같은 3개의 노드, 같은 요소인데도 8이라는 요소를 탐색 할 때 왼쪽 편향 트리는 노드를 2번 거치는 연산을 하고, 오른쪽 그림의 이진 트리는 오른쪽으로 한 번 이동하는 연산만을 수행하면 됩니다. 이처럼 노드가 늘어날수록 그 차이가 커집니다.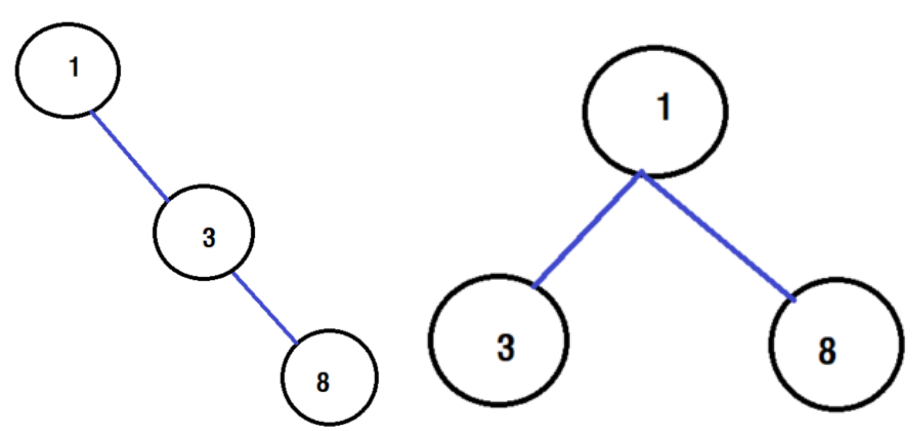이처럼 노드가 늘어나서 불균형해질수록 이진 트리의 연산횟수가 증가하는 단점이 있는데, 이 단점을 보완한 트리를 균형 이진 탐색 트리 혹은 균형 트리라고 합니다. 이 균형 트리에는 B 트리, AVL 트리, 2-3-4 트리 등이 있는데 오늘은 이 중에서 AVL 트리에 대해서 알아보려고 합니다.

AVL 트리 Adelson-Velskii, Landis Tree

AVL 트리는 균형 트리의 한 종류입니다. 이때 균형을 맞추기 위해서 균형 인수(Blance Factor)라는 것을 이용합니다. 균형 인수는 왼쪽 서브 트리의 높이와 오른쪽 서브 트리의 높이를 이용해서 계산합니다.

균형 인수 = 왼쪽 서브 트리 높이 - 오른쪽 서브 트리 높이

이 균형 인수를 이용해서 왼쪽과 오른쪽 서브 트리의 높이 차가 1 이하인 트리를 AVL 트리 라고 합니다. 즉, 균형 인수는 -1, 0, 1 이렇게 세 가지 숫자만 가질 수 있습니다.

실제로 트리에서 균형 인수를 구해보면 다음과 같습니다. 구할때 각 노드에서 서브 트리의 높이를 뺀 것이 해당 노드의 균형 인수가 됩니다.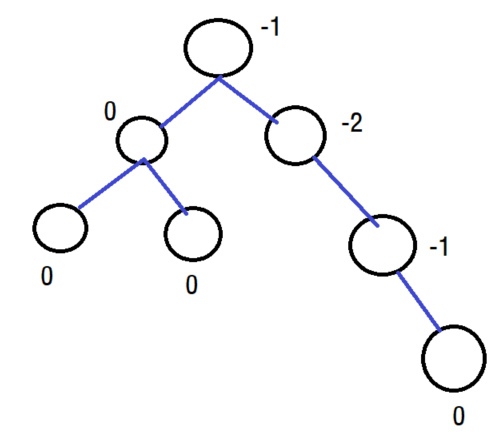

AVL 트리의 회전

AVL 트리는 균형 인수에 따라서 트리의 균형을 맞춥니다. 균형을 맞추기 위해서 노드의 균형 인수를 확인 한 후 트리를 재구성 해주는 작업이 필요합니다. 이때 재구성에 이용하는 연산이 회전 연산입니다. 회전은 오른쪽(R)과 왼쪽(L) 방향으로 회전합니다.

재구성에서는 총 4가지의 유형이있고 그에 따른 4가지 회전 연산이 있습니다.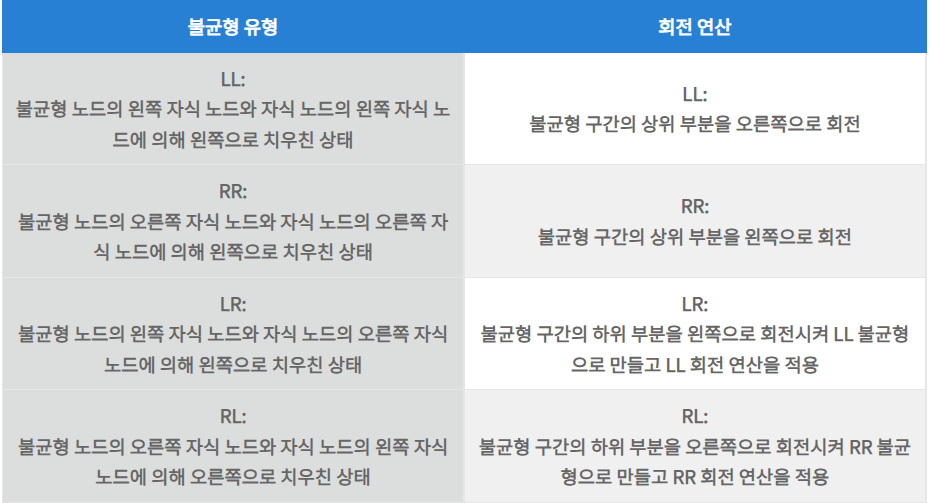

AVL 트리 구현

노드 정의

이제 AVL 트리를 구현해 보겠습니다. 우선 노드를 정의할 건데, 역시 양방향 노드를 사용합니다.

typedef struct avlTreeNode {
	int key;
	struct avlTreeNode* leftNode;
	struct avlTreeNode* rightNode;
}avlTreeNode;

회전 연산

AVL 트리 구현의 핵심인 회전 연산입니다. 4가지 방식이 있으므로 4가지를 전부 구현합니다.

LL 회전 연산

LL 회전은 왼쪽 자식 노드를 루트 노드로 만들고 기존 루트 노드를 새 루트 노드(기존 왼쪽 자식 노드)의 오른쪽 자식 노드로 만들어줍니다.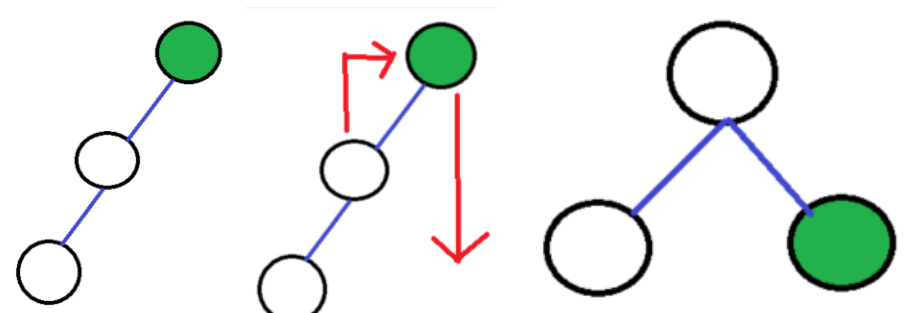

avlTreeNode* LL_rotate(avlTreeNode* parent) {
	avlTreeNode* child = parent->leftNode;

	//기존 루트 노드인 parent의 왼쪽 노드를 비웁니다.
	parent->leftNode = child->rightNode;
    //새 루트 노드가 된 child의 오른쪽 노드에 기존 루트노드를 연결합니다
	child->rightNode = parent;

	return child;
}

RR 회전 연산

LL 회전과 반대로, RR 회전은 오른쪽 자식 노드를 루트 노드로 만들고, 기존 루트 노드를 새로운 루트 노드(기존 오른쪽 자식 노드)의 왼쪽 자식 노드로 삽입합니다.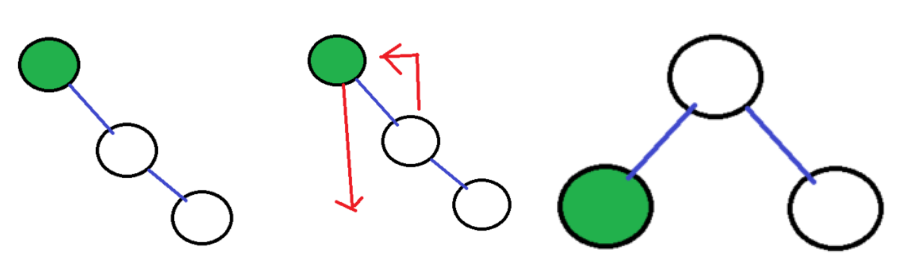

avlTreeNode* RR_rotate(avlTreeNode* parent) {
	avlTreeNode* child = parent->rightNode;

	//기존 루트 노드의 오른쪽 요소를 비웁니다.
	parent->rightNode = child->leftNode;
    //새 루트 노드의 왼쪽 노드를 기존 루트 노드로 설정
	child->leftNode = parent;

	return child;
}

LR 회전 연산

LR 회전은 한 번의 회전 연산 이후에 추가적인 회전 연산이 필요할 때 이용합니다. LR 회전은 하위 부분을 RR 회전 시킨 후 다시 상위 부분을 LL 회전 시키는 연산입니다.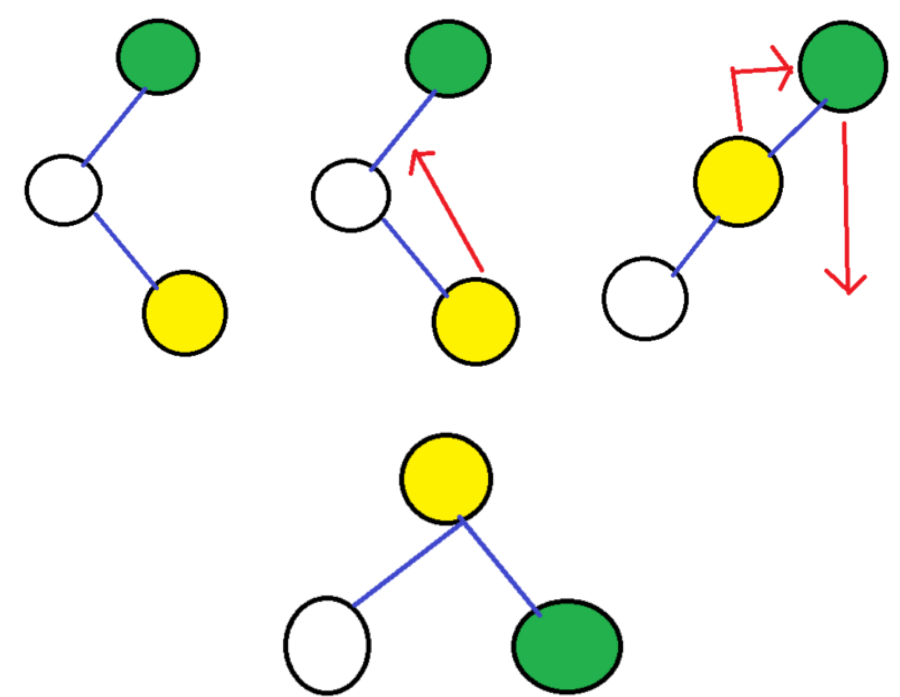

avlTreeNode* LR_rotate(avlTreeNode* parent) {
	avlTreeNode* child = parent->leftNode;

	//우선 왼쪽 서브 트리를 하위 부분 RR 회전 연산이 적용된 것으로 정렬
	parent->leftNode = RR_rotate(child);

	//마지막으로 LL 회전 연산을 해주면 LR 회전 완성
	return LL_rotate(parent);
}

RL 회전 연산

RL 회전 연산은 먼저 하위 부분을 LL 회전 한 뒤에 상위 부분을 RR 회전 시킨 회전 연산입니다.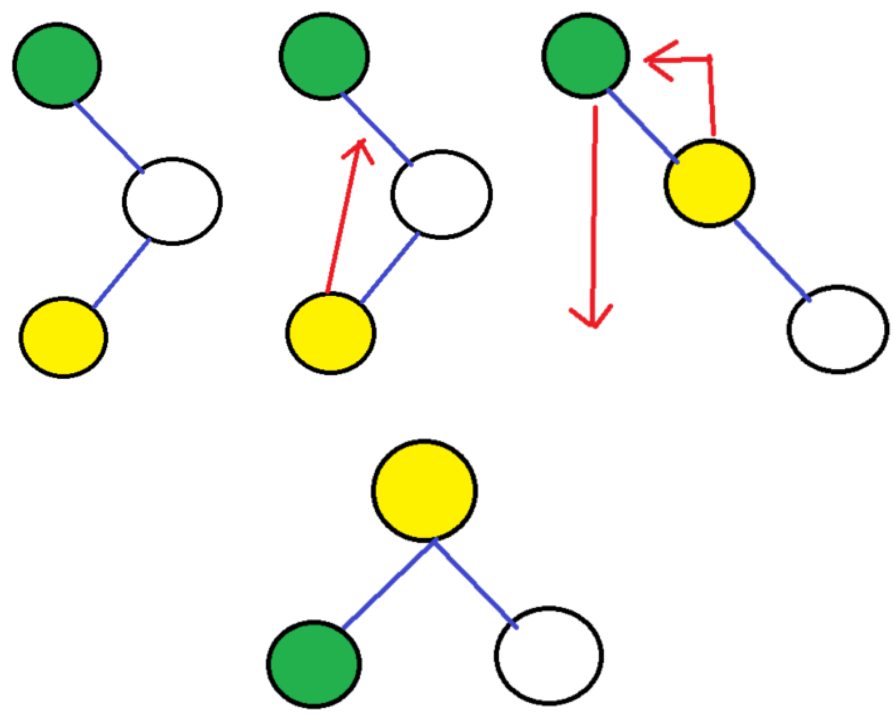

avlTreeNode* RL_rotate(avlTreeNode* parent) {
	avlTreeNode* child = parent->rightNode;

	//먼저 하위 부분을 LL 회전 시키고
	parent->rightNode = LL_rotate(child);

	//상위 부분을 RR 회전 시킨다
	return RR_rotate(parent);
}

균형 인수 구하기

회전을 시키기 위해 균형 인수를 활용 한다고 했습니다. 이제 트리에서 균형 인수를 구하는 방식을 알아보겠습니다.

//서브 트리의 높이를 구해서 반환 하는 함수
int getHeightOfSubTree(avlTreeNode* ptr) {
	int height = 0;

	if (ptr != NULL) {
    //오른쪽과 왼쪽 서브 트리 중 높은 값 +1이 트리의 높이입니다.
		height = MAX(getHeightOfSubTree(ptr->leftNode), getHeightOfSubTree(ptr->rightNode)) + 1;
	}

	return height;
}

//서브 트리의 높이를 통해 균형 인수를 구하는 함수
int getBalanceFactor(avlTreeNode* ptr) {
	if (ptr == NULL) {
		return 0;
	}

	//균형 인수 구하는 식을 통해서 균형 인수를 구합니다
	return getHeightOfSubTree(ptr->leftNode) - getHeightOfSubTree(ptr->rightNode);
}

균형 인수에 따라서 회전 연산 호출

균형 인수를 구했으니 이제 균형 인수 값에 따라서 올바른 회전 연산을 호출해야합니다.

avlTreeNode* rebalanceTree(avlTreeNode** ptr) {
	int balanceFactor = getBalanceFactor(*ptr);

	//균형 인수가 1 초과 시에는 왼쪽 불균형
	if (balanceFactor > 1) {
    //현재 노드의 왼쪽 서브 트리 균형 인수가 0 초과면 LL 회전 호출
		if (getBalanceFactor((*ptr)->leftNode) > 0) {
			*ptr = LL_rotate(*ptr);
		}
        //현재 노드의 왼쪽 서브 트리 균형 인수가 0 이하면 LR 회전 호출
		else {
			*ptr = LR_rotate(*ptr);
		}
	}
    //균형 인수가 -1 미만일 때는 오른쪽 불균형
	else if (balanceFactor < -1) {
    //현재 노드의 오른쪽 서브 트리 균형 인수가 0 미만 이면 RR 회전 호출 
		if (getBalanceFactor((*ptr)->rightNode) < 0) {
			*ptr = RR_rotate(*ptr);
		}
        //현재 노드의 왼쪽 서브 트리 균형 인수가 0 이상이면 RL 회전 호출
		else {
			*ptr = RL_rotate(*ptr);
		}
	}
	return *ptr;
}