cs231n Lecture 6 | Training Neural Networks I 강의 정리

✍ 해당 시리즈 포스팅은 스탠포드 대학의 cs231n 강의 내용을 정리한 글입니다.

Activation Functions

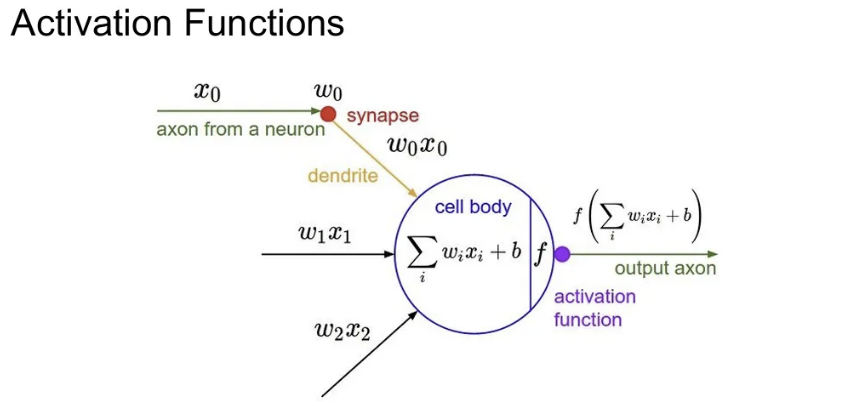
앞서 배웠듯, Conv layer나 FC layer 등을 거친 후에는 activation function을 통해 비선형 변환을 적용해주었음. 오늘은 다양한 활성함수의 종류와 그들 간의 Trade-off를 다뤄보자.

Sigmoid

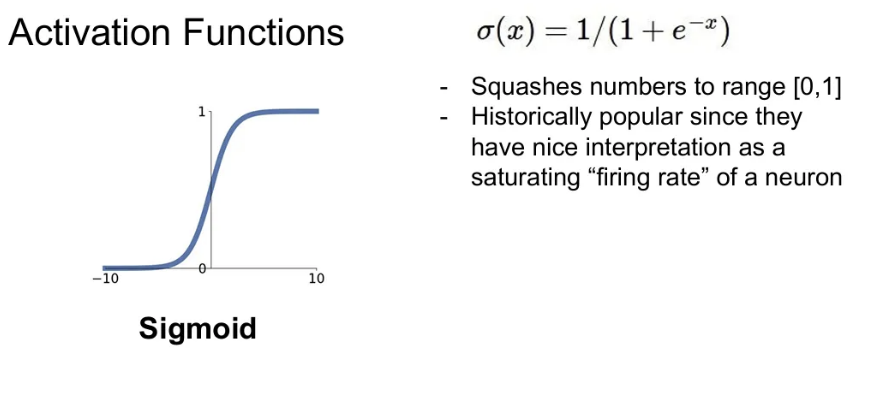
• 입력을 받아서 [0, 1] 사이의 값이 되도록 해준다.
• 입력 값이 클수록 1에, 작을수록 0에 가깝다.
• 뉴런의 firing rate를 saturation(포화) 시키는 것으로 해석 가능

단점

1. Vanishing Gradients

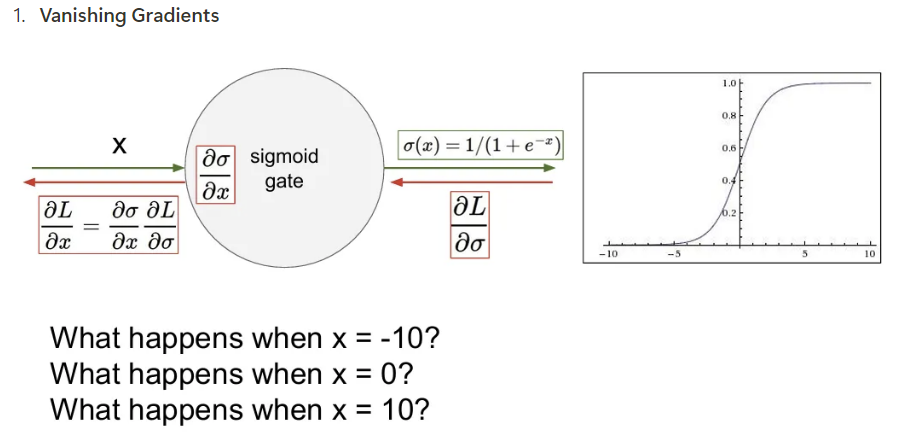
입력 X값이 큰 음의 값이나 양의 값(포화된 경우)을 가지게 되면 시그모이드 함수에서 flat한 부분이 되고, 이런 부분은 gradient가 거의 0에 수렴한다. 이런 값이 계속해서 backpropagation을 통해 곱해져 간다면 gradient가 죽어버리고, 하류로 계속 넘어가게 됨.

2. Not zero-centered

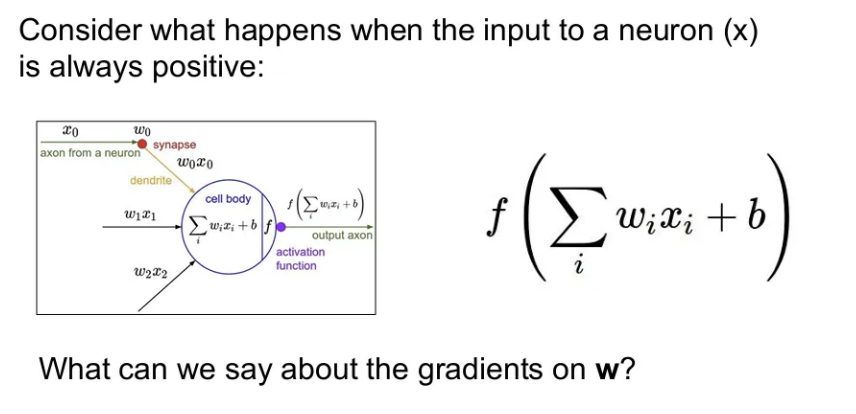
위 구조에서 $w$에 대한 $f$의 미분값은 $x$값 자체가 되는데, 만약 input $x$값이 양수로만 이루어져있다면, 뒤에서 backprop 된 gradient와 local gradient를 곱해서 나오는 gradient의 부호는 변하지 않는다. 이는 $w$가 모두 같은 방향으로만 움직일 것을 의미. 파라미터를 업데이트 할 때 다같이 증가하거나 다같이 감소하게 된다.

그렇게 되면 좌표평면을 그렸을 때 1사분면이나 3사분면 방향으로만 업데이트가 가능하게 되고, 만약 최적의 $w$가 4사분면에 있었다면 sigmoid의 gradient로는 도달 불가능하다. → 우리가 zero-mean 데이터를 원하는 이유. ($x$값이 음수/양수 다양)

3 . Exp() is a bit compute expensive

지수함수 연산 계산 비용이 다른 연산에 비해 큰 편이다. 하지만, 큰 틀에서 보면 내적 같은 연산에 비해서는 계산 비용이 그렇게 큰 건 아니라, 큰 문제는 아니라고 함

Tanh

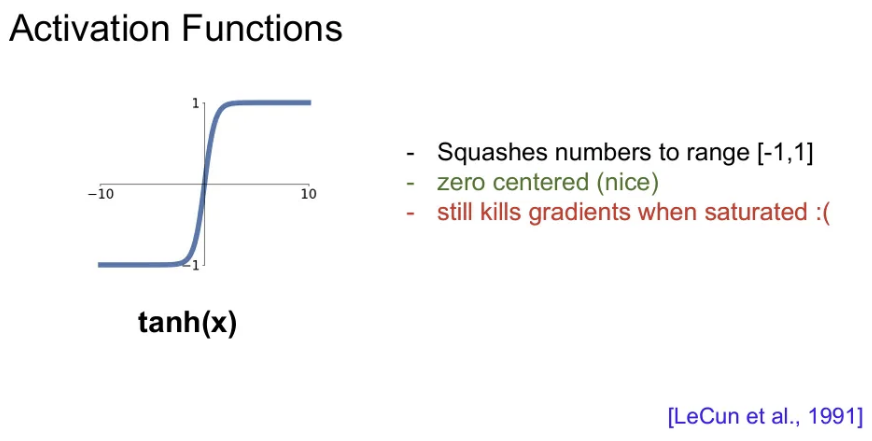
• sigmoid랑 유사하지만 범위가 [-1, 1] 로 다르다.
• zero-centered를 만족함.
• 여전히 gradient vanishing 문제가 발생한다.

ReLU (Rectified Linear Unit)

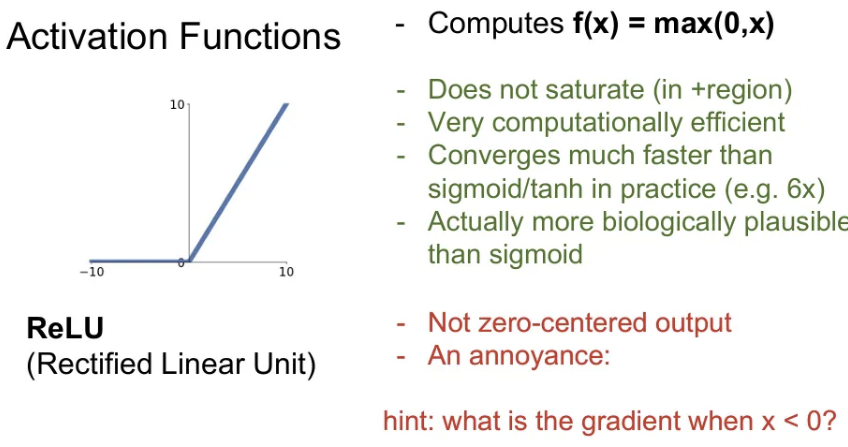
• 입력이 음수면 0을 내보내고, 양수면 입력 값 그대로 출력한다.
• 적어도 양의 입력값들은 saturation 되지 않는다. (가장 큰 장점)
• 단순 max 연산으로 계산이 빠름.

단점

1. zero-centered가 아니다.
2. 음의 input인 경우엔 saturation되어 gradient 절반은 죽는다.

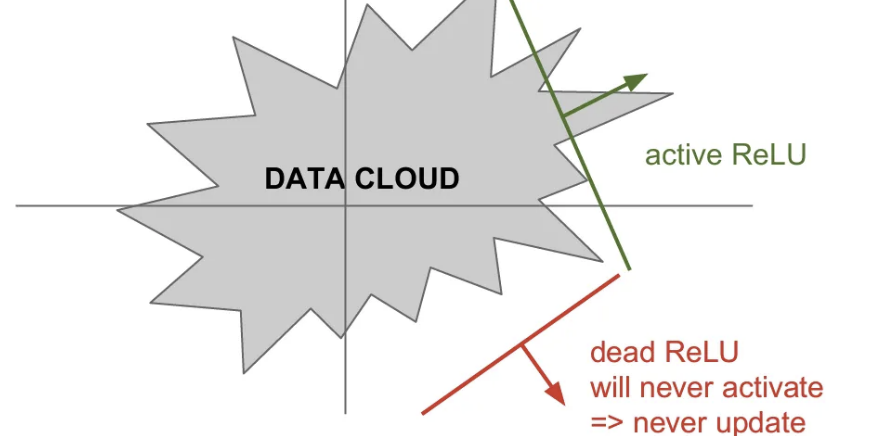
위 그림 처럼 Training set에 대한 Data cloud가 있고, $W_1 X_1 + W_2X_2$와 같은 선형식에 ReLU 연산을 통과했을 때 가중치로 이루어지는 hyperplane에 따라 반은 positive, 반은 negative가 된다. 이 때 ReLU의 연산으로 생긴 초평면으로 그 어떤 값도 activate가 되지 않고 이에 따라 업데이트도 되지 않는다면 이를 Dead ReLU라고 하고, activate 되는 값이 있다면 Active ReLU라고 한다. 이를 위해 0.01 정도의 positive bias를 추가해주는 경우도 있다.

보통 Dead ReLU는 가중치 초기화를 잘못하거나, Learning rate를 너무 크게 잡는 경우 발생하게 된다. 보통 실제로 학습을 다 시켜 놓은 네트워크를 살펴보면 10~20%가량은 dead ReLU가 되어 있다고 한다.

Leaky ReLU

• negative space에서도 기울기를 살짝 주어 saturation이 발생하지 않음
• 여전히 계산 효율적
• Dead ReLU 더 이상 발생하지 않음

PReLU (Parametric Rectifier)

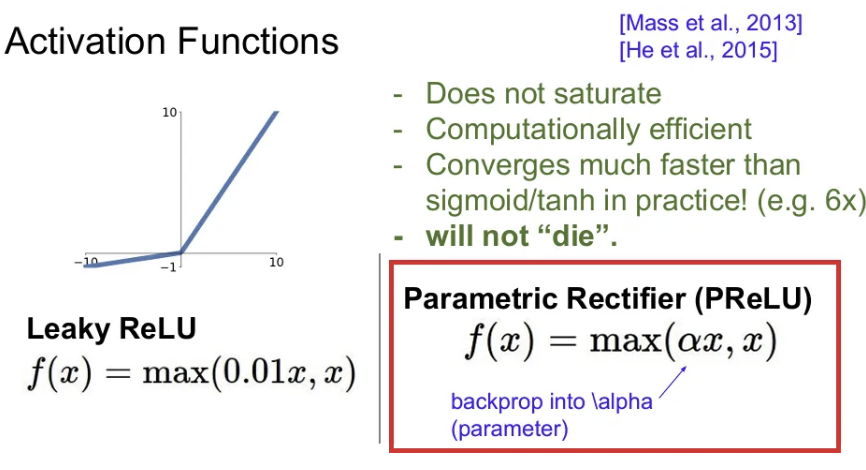
• Leaky ReLU와 같은 방식으로 negative space에서도 일정한 기울기를 주되, 이를 학습 파라미터 $\alpha$로 정의한다.
• 만약 $\alpha$를 0.01로 설정하고 학습시키지 않는다면 Leaky ReLU와 동일하다.

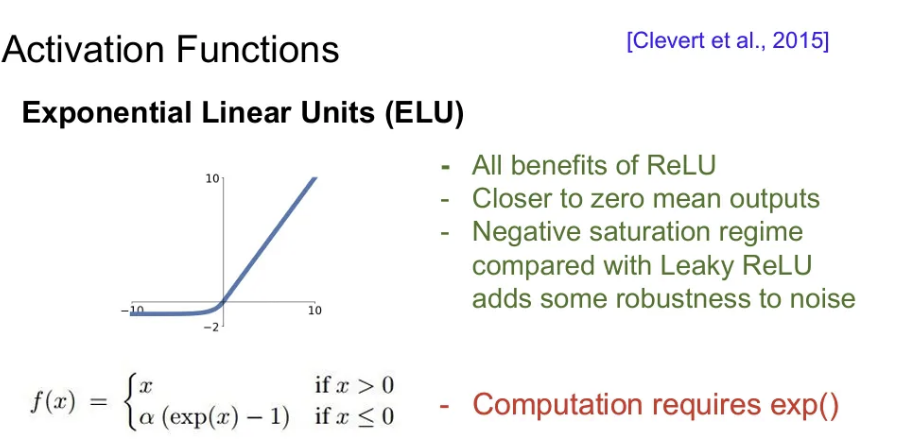
• zero-mean 에 가까운 출력값을 보인다.
• Leaky ReLU와 비교했을 때, negative space에서 또 다시 saturation된다.
• 오히려 이런 saturation으로 인한 deactivation이 노이즈에 강할 수 있다는 주장
• ReLU와 leaky ReLU의 중간 정도
• exp 연산이 있어서 느린 편이다.

Maxout Neuron

• 두 개의 $w$에 $x$를 내적한 값에 bias term을 더한 값 중 최대값을 사용한다.
• ReLU와 Leaky ReLU의 좀 더 일반화된 형태
• saturation 되지 않아 gradient가 죽지 않음.
• 뉴런 당 두 개의 weight를 가져야 하기 때문에 파라미터 수가 두 배로 늘음

TLDR: In practice:

• 보통 ReLU를 많이 사용하지만 learning rate를 조심히 설정할 것
• Leaky ReLU, Maxout, ELU를 사용해볼 것
• Tanh를 사용 해보되, 큰 기대는 하지 말 것
• sigmoid는 웬만하면 사용 x

강의 시점은 2017년이고, 포스트를 작성하는 시점 2024년에서는 여전히 ReLU 및 이에 대한 변형식들은 일반적이지만, Swish나 Mish 등 다양한 activation function들이 추가되었다.

Data Preprocessing

보통 데이터 전처리를 할 때 Normalization을 수행하는데, 원본 $X$에서 평균을 뺀 뒤 표준편차로 나눠주게 되면 모든 차원이 범위 안에 있게 하여 동등한 기여를 하게 변환해주기 때문. 실제로 이미지의 경우엔 이미 각 차원 간에 스케일이 어느정도 맞춰져 있기 때문에, zero-centering까지만 수행하는 경우가 많다고 한다.

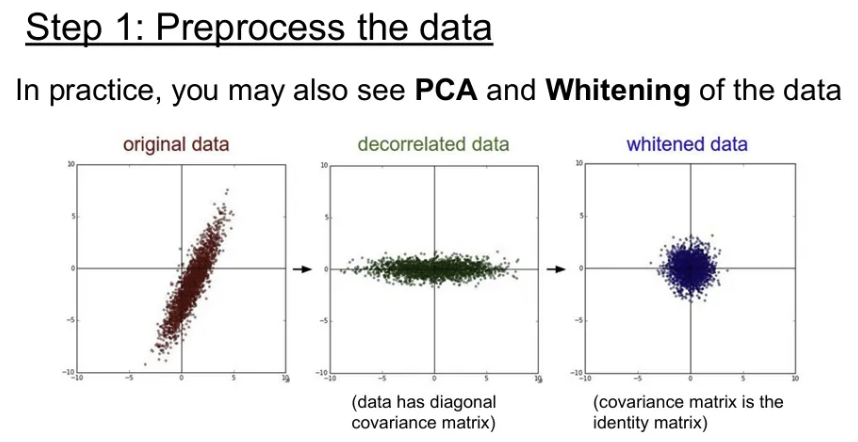
일반적인 머신러닝 관점에서는 PCA나 Whitening을 많이 사용하기도 하지만, 앞서 언급했듯 이미지에서는 굳이 활용하지 않는 경우가 많다.

※ Test set에서도 Training과 같은 방식으로 전처리를 해주어야 하는데, zero-centering을 수행할 때 당연히 Training data의 평균을 그대로 사용해서 빼주어야 함.

Zero-centering을 수행할 때 AlexNet의 경우에는 이미지에서 3개의 채널 통틀어서 평균을 빼 주었고, VGGNet에서는 채널 별로 평균을 따로 구해서 빼주었다고 한다. 어떤 방식을 활용할 지는 우리 판단하기 나름. 미니 배치를 사용하더라도, 전체 Training set의 평균을 사용하면 된다.

Q. 만약 전처리 과정에서 zero-centering을 수행해주면 시그모이드의 Not zero-centered 문제를 해결할 수 있지 않을까?

A. 이는 단순히 첫번째 layer 에서만 해결. 그 다음 layer부터는 다시 zero-centered를 만족하지 못한다.

Weight Initialization

만약 초기 모든 Weight 값들을 0으로 초기화하면 어떻게 될까?

→ 모든 뉴런은 다 같은 연산을 수행하게 된다. 출력도 모두 같고, gradient도 같게 돼서, 결국 모든 가중치가 똑같은 값으로 업데이트 됨.

1. 초기 Weight값들을 평균 0, 표준편차 1e-2의 작은 랜덤 값들로 초기화

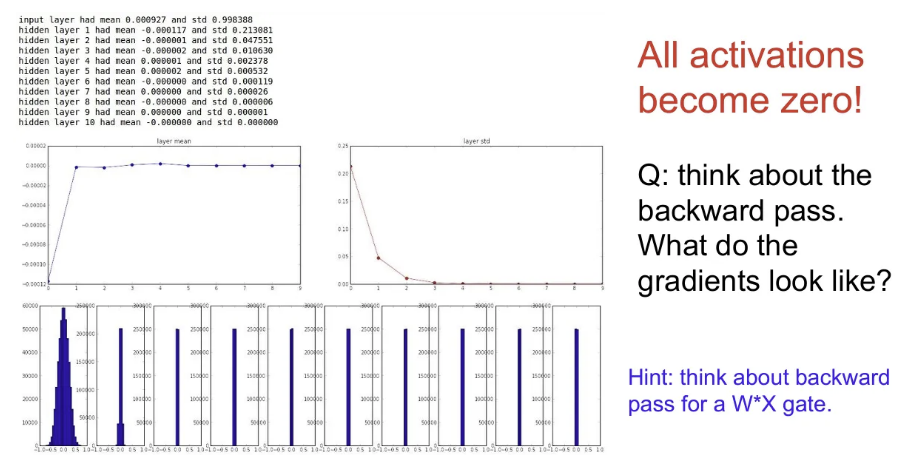
• 얕은 신경망에서는 잘 작동하지만, 네트워크가 깊어지게 되면 금방 표준편차가 0이 돼버린다. $W$를 곱하면 곱할수록 그 값이 너무 작아서 출력 값이 급격히 줄어들게 되고, 결국 0이 돼버린다.
• Backpropagation 관점에서도, $W\times X$ 게이트를 지날 때 local gradient는 $X$가 되고, 당연히 이를 상류 gradient와 곱해서 하류로 넘겨주게 되면 마찬가지로 업데이트가 잘 되지 않는다.

2. 초기 Weight값들을 평균 0, 표준편차 1의 랜덤 값들로 초기화

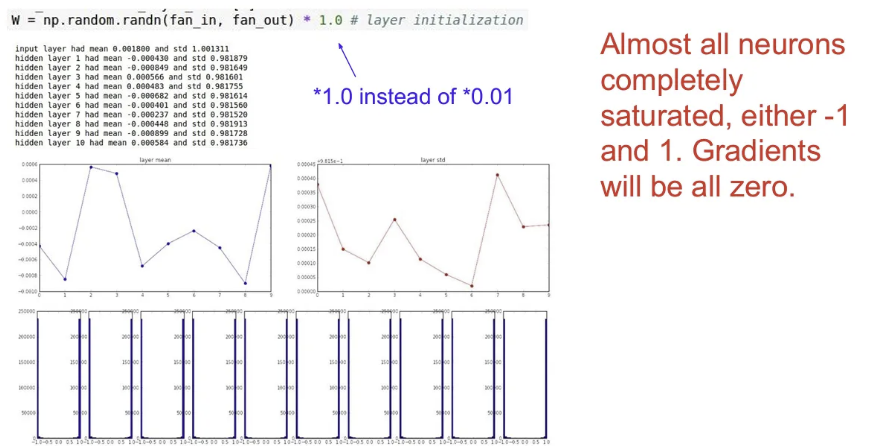
• 가중치가 큰 값을 가지기 때문에 tanh를 적용하게 되면 바로 saturation 된다. (출력으로 -1이나 1을 갖게 됨)
• 당연히 gradient는 0이 되고 업데이트는 일어나지 않는다.

3. Xavier initialization

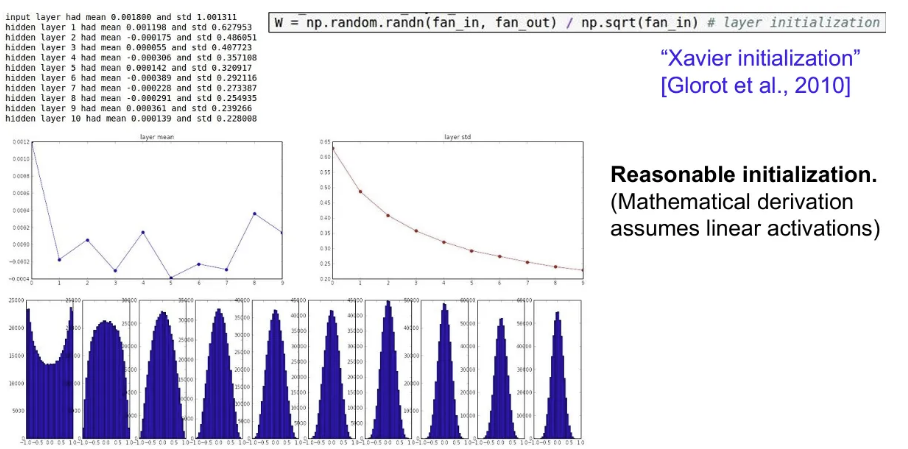
• 표준 정규분포로 뽑은 값을 데이터 입력의 수(n)로 스케일링
• 입력 데이터의 분산이 출력에서도 유지되도록 한다.
• 만약 입력의 수가 작으면 더 작은 값으로 나눠지게 되고, 출력 데이터의 분산을 입력 데이터와 맞춰줘야 하기 때문에 자동으로 $W$에는 더 큰 값들을 가지게 된다.
• 활성 함수가 선형임을 가정한다.
• ReLU를 사용하면 출력의 절반을 죽이기 때문에 출력의 분산이 반 토막 나서 잘 작동하지 않는다.

4. He initialization

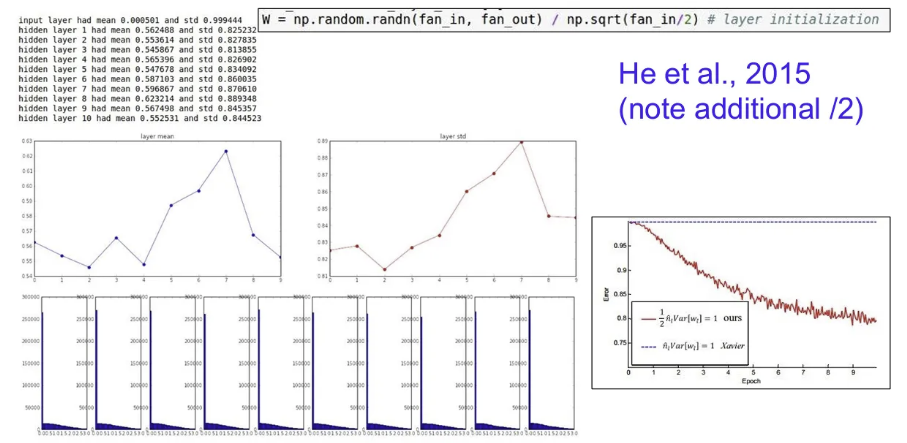
• Xavier initialization에서 활성화 함수로 ReLU를 사용할 때 출력의 분산이 반으로 줄어든다는 것을 고려하여, 가중치 분산을 두 배로 키워준다.

Batch Normalization

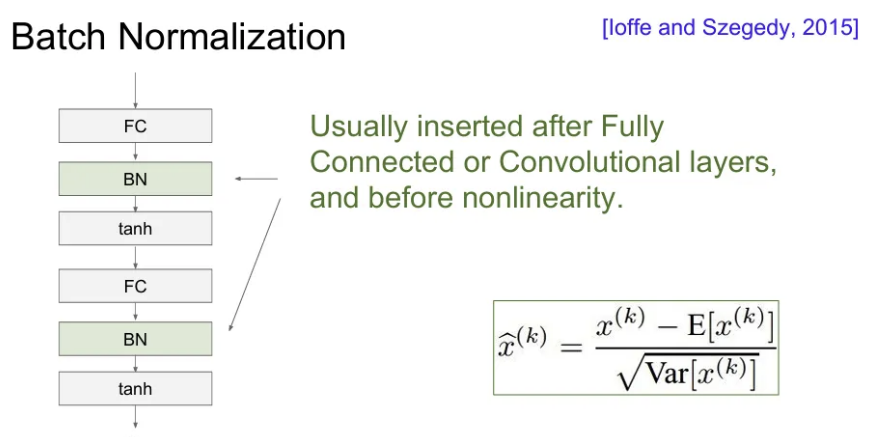
• 가중치를 잘 초기화 시키는 것도 중요하지만, 현재 (미니)배치의 평균과 분산을 이용해서 activation 값을 Unit Gaussian으로 정규화 해주는 방법
• 평균과 분산을 상수로 가지면 언제든 미분 가능하여 역전파 가능
• 보통 Fully Connected Layer나 Conv Layer 직후 활성화 함수 전에 넣어준다.
• 각 레이어의 $W$가 지속적으로 곱해져서 발생하는 Bad scaling effect를 상쇄해줌.
• 학습을 강건하게 해주며 learning rate를 키우거나 다양한 초기화 기법을 사용할 수 있게 해준다.
• 각 레이어의 출력은 해당 데이터 하나 뿐 아니라 배치 안에 존재하는 모든 데이터의 영향을 받기 때문에Regularization 역할도 해줌

1. 위 그림에서 배치 당 $D$차원, $N$개의 학습 데이터가 있으면, 각 차원(feature element) 별로 평균과 분산을 각각 구해준다.
2. 한 배치 내에서 이를 전부 계산하여 정규화(Normalization)한다.
   • Conv layer 직후 오는 경우에는 Activation Map(depth)마다 평균과 분산을 하나만 구해서 정규화를 진행한다.

아래는 3x3 행렬을 입력했을 때 정규화 과정 예시이다.

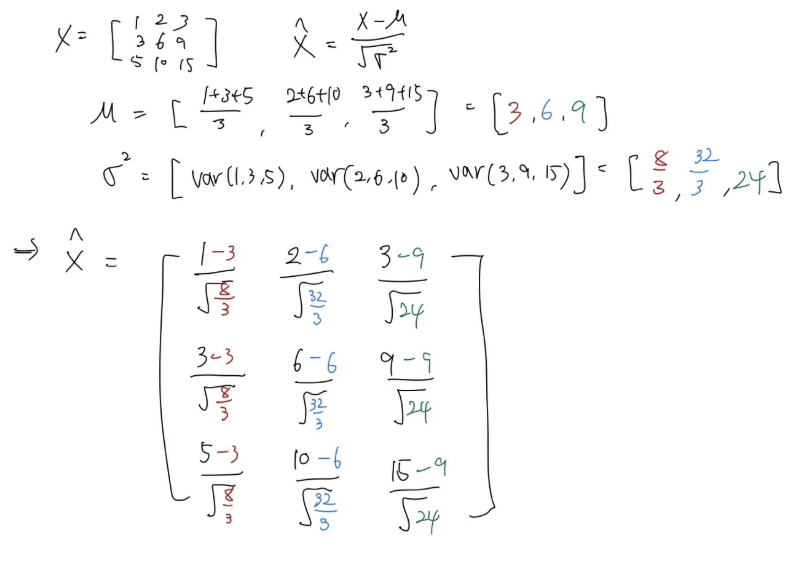
Tanh 함수를 예시로 activation function을 적용하기 전 Batch Normalization을 적용해주는 이유는 normalization을 통해서 Input이 Tanh의 linear한 영역(0에 가까운 부분)에서만 존재하도록 하기 위함. 그렇게 되면 saturation은 전혀 발생하지 않게 만들어줄 수 있다.

그렇다면 이를 좀 더 일반화해서, saturation이 아예 발생하지 않는 것 보다, 얼마나 일어날 지를 조절 할 수 있으면 더 좋을 것이고, 이를 위해 학습 가능한 $\gamma$ 라는 scaling term과 $\beta$라는 shifting term을 추가한다. 이를 통해 $\gamma$는 분산, $\beta$는 평균이 쓰이면 정규화된 값을 다시 원상복구 될 수도 있다(그냥 거꾸로 연산한다 생각!). 하지만 이는 극단의 경우에 그럴 수도 있다 일 뿐. 실제로는 그럴 일 없다고 한다.

그렇다면 Test 때 Batch Normalization은 어떻게 이루어질까?

→ 예전 머신러닝에서 데이터의 정규화 및 표준화를 진행할 때도 Training 과정에서 학습된 scaler를 그대로 Test set에서도 활용하듯이, Test set에서의 Batch Normalization은 평균과 분산을 해당 Test 데이터 셋에서 구하는 방식이 아니라, Training time에 running averages 같은 방법으로 평균 및 분산을 계산하고 사용한다고 한다.

Babysitting the Learning Process

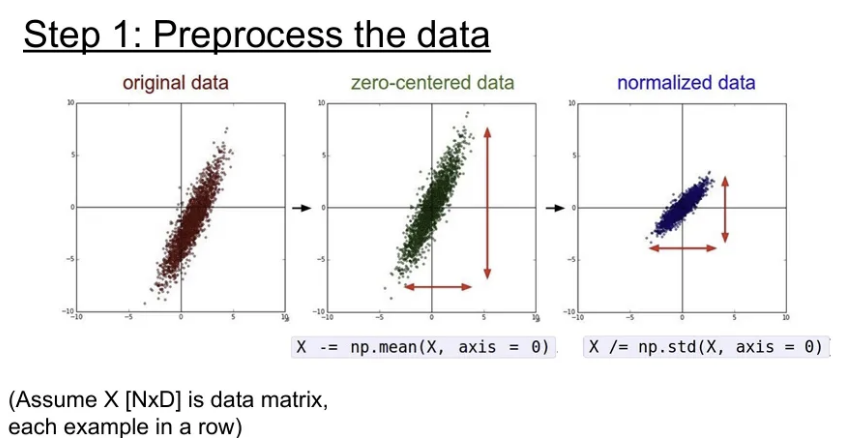
1. 데이터 전처리 (이미지에서는 주로 zero-centering)

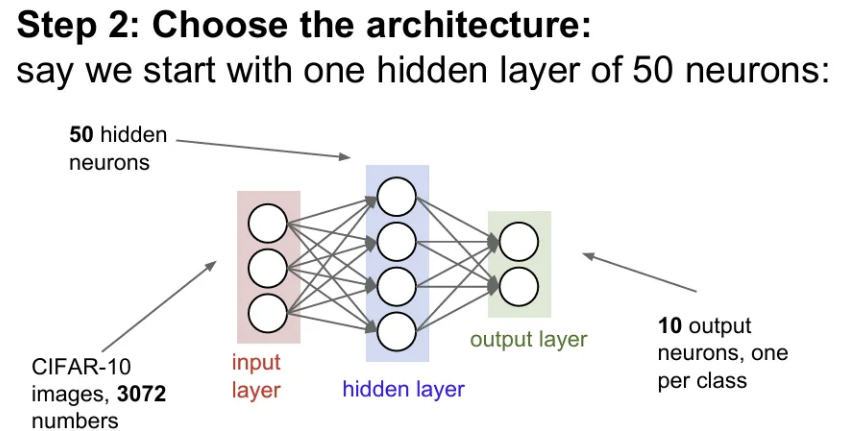
2. 사용할 아키텍처 선택

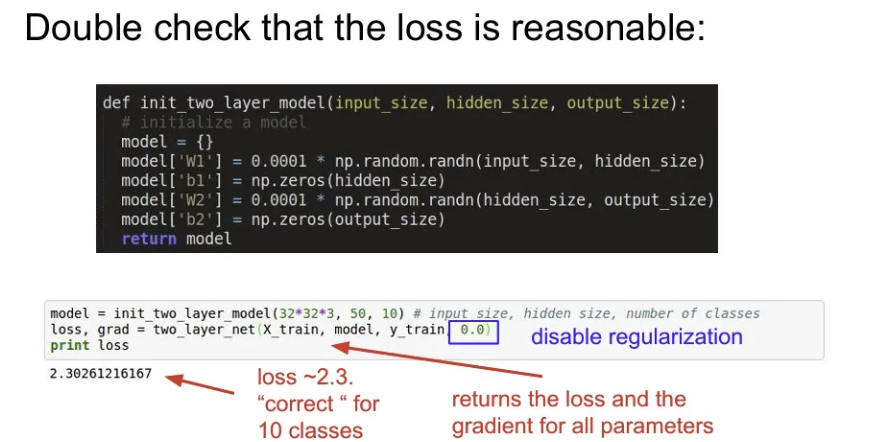
3. 네트워크를 초기화. Forward pass 후에 Loss가 적절한지 확인해야 함. 처음에는 regularization을 0으로 설정

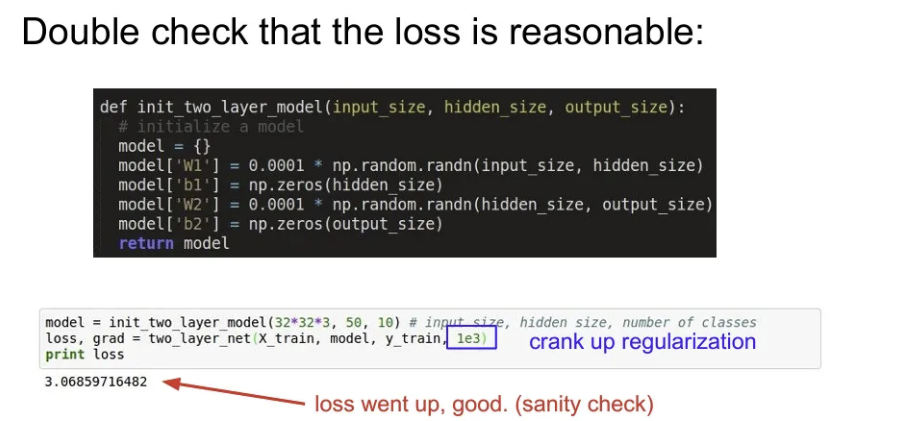
4. loss에 Regularization term을 추가했을 때 loss 값이 이전보다 증가했는지 확인

5. 데이터의 극히 일부만 활용해서 학습하여 loss가 많이 줄어드는지 확인. 데이터가 적으니 오버피팅되면서 training에서는 loss가 줄어들어야 정상(regularization은 X)

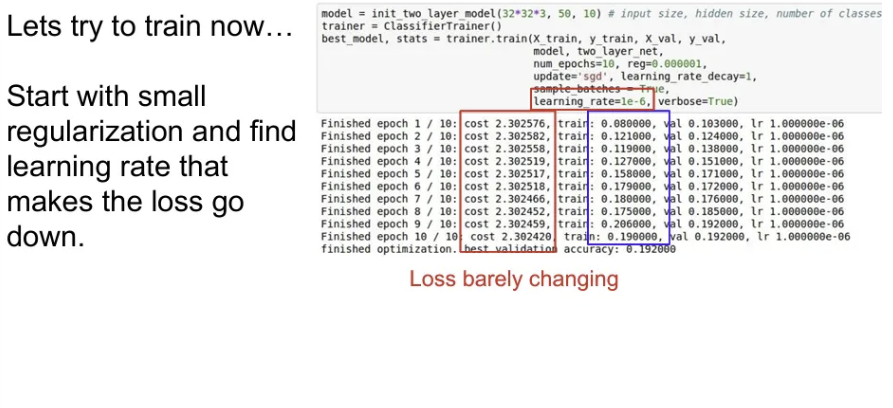
6. 작은 Regularization을 추가하고, 적절한 learning rate를 찾는 과정을 거친다. Learning rate가 너무 적다면 gradient 업데이트가 충분하지 않고, 너무 크면 날뛰게 된다. 보통은 1e-3에서 1e-5 사이에서 활용

Hyperparameter Optimization

Cross Validation

하이퍼파라미터 최적화에 있어서 자주 사용되는 방법. Train set으로 학습하고 Validation set으로 평가한다.

1. Coarse stage
   • 넓은 범위에서 값을 골라내서 적은 epoch 만으로도 잘 동작하는 구간(어떤 하이퍼파라미터가 효과적인지)을 확인한다.
2. Fine stage:
   • Coarse stage를 통해 대충 어느 범위에서 잘 동작할 지를 파악했으면, Fine stage에서는 좀 더 좁은 범위를 설정하고 학습을 더 길게 시켜본다. 이 때 epoch 마다 cost가 증가한다면 잘못되고 있는 것을 파악하고 바로 다른 하이퍼파라미터 테스트로 넘어가기

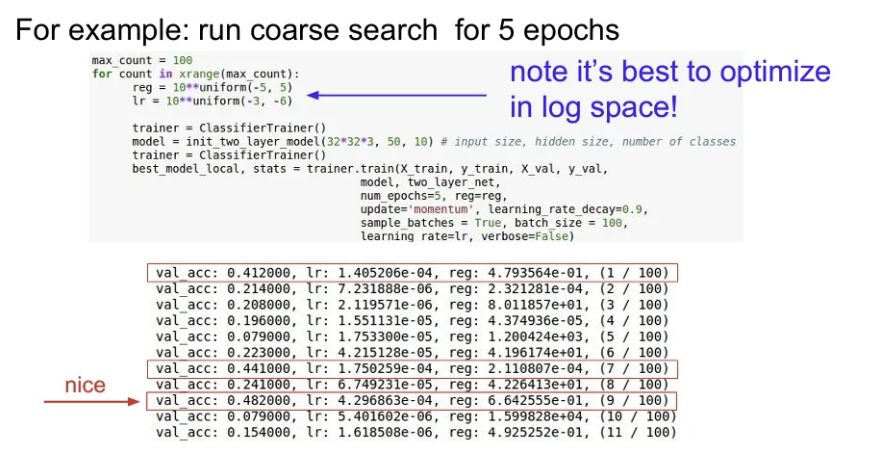
예를 들어, 위와 같이 regularization과 learning rate를 하이퍼파라미터로 넓은 범위에서 cross validation을 먼저 수행해서 validation accuracy가 높았던 경우의 하이퍼파라미터 구간을 파악한다.

이후 하이퍼파라미터의 구간을 좁혀서 다시 fine stage를 수행.

하지만 지금처럼 fine stage를 진행했을 때 정확도가 높았던 경우의 learning rate들이 우리가 좁혀 설정한 범위의 경계 부분에 집중되어있는 것을 확인할 수 있다. 이런 경우 최적의 learning rate가 현재 범위에 속하지 않는 바로 옆 구간에 존재할 가능성이 높다고 볼 수도 있다. 최적의 하이퍼파라미터 값들이 다시 정해준 범위의 중앙 쯤에 위치하도록 하는 것이 중요하다.

Random Search vs Grid Search

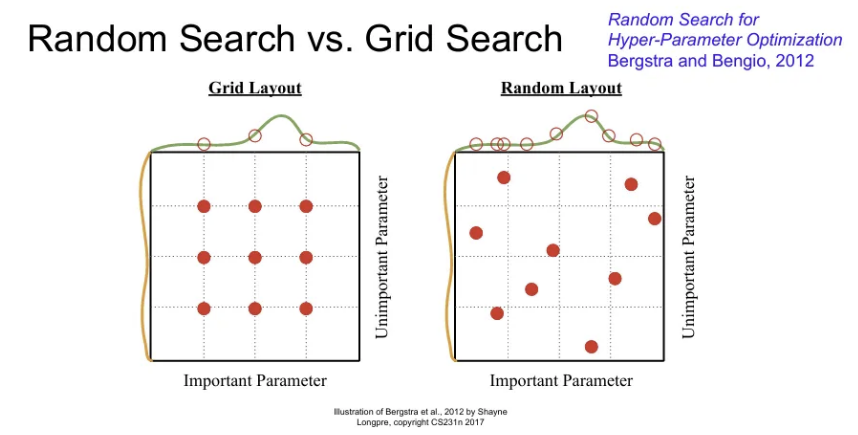
Grid Search는 하이퍼파라미터를 고정된 값과 간격으로 샘플링 방식인데, 이보다는 위 코드 예시로 활용하였던 특정 범위 내 uniform distribution에서 랜덤 샘플링을 하는 Random Search가 대체로 효과적이다.

→ 내 모델이 예를 들어서 위 그림에서 노란색 하이퍼파라미터 보다는 초록색 하이퍼파라미터의 변화에 더 민감하다고 했을 때, Random Search는 이 초록색 하이퍼파라미터로 인해 변화하는 함수를 더 잘 찾을 수 있다. 결과적으로 더 중요한 변수에서 더 다양한 값을 샘플링 가능하다.

Reference

• 유튜브 : https://www.youtube.com/watch?v=d14TUNcbn1k&list=PLC1qU-LWwrF64f4QKQT-Vg5Wr4qEE1Zxk&index=6
• PDF: https://cs231n.stanford.edu/slides/2017/cs231n_2017_lecture6.pdf