https://arxiv.org/abs/2106.13008

1. Introduction

Real-world applications에서, 장기적인 계획과 조기 경보를 위해 예측 기간을 먼 미래까지 확장하는 것은 중요한 과제이고, 이러한 장기 시계열 예측 문제는 예측해야 할 시계열의 길이가 매우 길다는 특징을 가지고, 아래와 같은 어려움이 있다.

1. 복잡하게 얽힌 시간적 패턴으로 인해 종속성이 가려져 long-term time series로 부터 직접적으로 시간적 종속성을 찾는 것은 신뢰성이 낮다.
2. Self-attention을 쓰는 전통적인 Transformers는 시퀀스 길이에 대해 제곱식의 complexity를 가지므로, long-term forecasting에 적용하기엔 비용이 너무 크다.

저자들은 decomposition을 전처리에서만 사용하는 것이 아니라, 심층 예측 모델이 점진적인 decomposition을 내재적으로 수행할 수 있는 generic architecture를 제안한다.

---

2. Related Work

2.1. Models for Time Series Forecasting

• ARIMA (AutoRegressive Integrated Moving Average)

  • Differencing(차분)을 통해 Non-stationary 시계열 데이터를 stationary하게 변환한 후 예측 수행

• RNN-based methods

  • Temporal dependencies를 모델링하기 위해 사용 (DeepAR, LSTNet, Attention-based RNNs···)

• TCN (Temporal Convolution Networks)

  • Causal convolution을 활용하여 temporal causality를 모델링

• Transformers based on the self-attention mechanism

  • 최근 NLP, Audio processing, Computer vision 등 다양하게 활용되지만, long-term time series에서 $O(L^2)$의 시간복잡도를 가져 적용이 힘듦

  • 이를 해결하기 위해, 기존 연구들은 sparse attention을 도입 (LogTrans, Reformer, Informer···)

    • 이들은 point-wise dependency와 aggregation을 기반으로 하여 long-term time series forecasting에서 정보 활용도가 제한적
    • 또한, 자연스러운 시계열 패턴을 반영한 구조가 부족
    
    

→ 본 논문에서는 Self-Attention을 Auto-Correlation으로 대체하여 시계열의 고유한 주기성 및 series-wise connection을 제공

2.2. Decomposition of Time Series

Time series Analysis의 표준 방법으로, 시계열을 여러 구성 요소로 분해하여 각각이 더 예측 가능한 기본 패턴 카테고리 중 하나를 나타내도록 한다.

예측 task에서 decomposition은 항상 미래 time series를 예측하기 전 과거 시계열에 대한 pre processing으로써 사용된다.

• Prophet은 trend-seasonality decomposition을 사용
• N-BEATS는 basis expansion을 사용
• DeepGLO는 matrix decomposition을 사용

하지만 이러한 pre-processing은 과거 시계열의 plain decomposition effect에 의해 제한되며, long-term future에서 시계열의 기본 패턴 간 계층적 상호작용을 간과함.

→ 본 논문에서는 decomposition의 아이디어를 deep model의 inner block으로써 사용하여 전체 예측 과정에서 hidden series를 점진적으로 분해할 수 있도록 한다. 이는 과거 시계열 뿐 아니라 예측된 중간 결과에도 적용

---

3. Autoformer

시계열 예측 문제는 길이 $I$의 과거 시리즈를 받아서 길이 $O$의 미래 시리즈를 예측하는 것으로, long-term forecasting은 더욱 큰 $O$를 갖는 미래 시리즈를 예측하는 작업이다. 이는 복잡한 temporal pattern을 처리하고, 계산 효율성 및 정보 활용의 bottleneck을 해결하는 데 어려움이 있다. 이 두 문제를 해결하기 위해 저자들은 decomposition architecture로써 Autoformer를 제안하고, period 기반 종속성의 발견 및 주어진 기간에서 유사한 sub-series를 통합하기위한 Auto-Correlation mechanism을 디자인하였다.

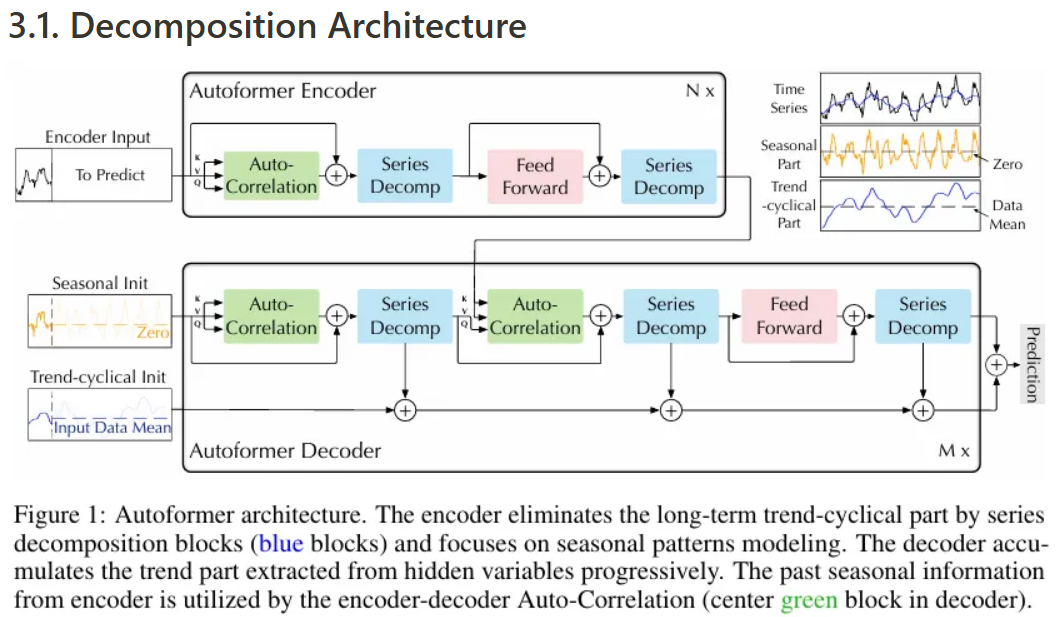
3.1. Decomposition Architecture

저자들은 Transformer를 deep decomposition architecture로 개편하고, 이에는 inner series decomposition block과 auto-correlation mechanism, 그리고 이에 대응하는 Encoder와 Decoder가 포함된다.

Series decomposition block

장기 예측 환경에 있어서 복잡한 temporal pattern을 학습하기 위해, 저자들은 series를 trend-cyclical(추세-순환) 및 .seasonal(계절성) 파트로 분리하는 decomposition idea를 적용한다.

이 두 파트는 각각 series의 long-term progression과 seasonality를 보여준다. 하지만 미래 데이터를 모른다고 가정해야 하기 때문에, 미래 series를 직접 decomposing 하는 것은 불가능하여 저자들은 Autoformer의 inner operation으로 series decomposition block을 도입하는데, 이는 전체 아키텍처 figure에서 파란 블럭 부분이다.

해당 블럭은 예측된 중간 hidden 변수에서 long-term stationary trend를 점진적으로 추출할 수 있다.

길이 $L$의 input series $\mathcal X(\in \mathbb R^{L \times d})$ 가 주어지면, trend-cyclical part인 $\mathcal X_t$와 seasonal part인 $\mathcal X_s$는 위와 같이 구해진다. (Series decomposition) 여기서 Average pooling은 moving average를 위해 적용하고, padding은 series 길이를 유지하기 위해 사용한다.

Model inputs

Encoder의 입력은 과거 $I$개의 time steps를 포함하는 $\mathcal X_{en} \in \mathbb R^{I \times d}$ 이고, decoder의 input은 seasonal part인 $\mathcal X_{des} \in \mathbb R^{(\frac I2 + O) \times d}$ 와 trend-cyclical part인 $\mathcal X_{det} \in \mathbb R^{(\frac I2 + O) \times d}$ 가 포함되고 이 값들은 정제되는데, 각각의 initialization은 아래와 같이 공식화된다.

여기서 $\mathcal X_{ens}$와 $\mathcal X_{ent}$ 는 $\mathcal X_{en}$의 마지막 절반에서 series decomposition을 통해 만들어지므로 ${\mathcal X_{ens}, \mathcal X_{ent} \in \mathbb R^{\frac I2 \times d}}$ 이고, $\mathcal X_0, \mathcal X_{Mean} \in \mathbb R^{O \times d}$는 각각 0과 $\mathcal X_{en}$의 평균으로 채워진 placeholders이고, 이들을 concat했기 때문에 $\mathcal X_{des} \in \mathbb R^{(\frac I2 + O) \times d}$, $\mathcal X_{det} \in \mathbb R^{(\frac I2 + O) \times d}$인 것.

그림판으로 대충 표현하느라 예쁘진 않지만, 대충 위 같은 크기의 input이 들어온다고 생각하면 될 것 같다. Encoder input 부분에서 To Predict 부분은 사실 없는 부분이고, 아래 decoder에서 예측할 부분과 맞춰주기 위해 그림에는 같은 길이 $O$만큼 이어 붙여 놓은 것 같다.

Encoder

Encoder는 주로 seasonal part modeling에 집중한다. Encoder의 출력은 과거 seasonal information이 되고, 이는 cross information으로써 decoder가 예측 결과를 정제하는 데 사용될 수 있다.

총 $N$개의 encoder layers가 있고, $l$번째 encoder layer의 전체적인 수식은 $\mathcal X_{en}^l = Encoder(\mathcal X_{en}^{l-1})$ 로 표현될 수 있고, 세부 과정은 아래와 같다.

이는 위 fig에서 빨간 박스 친 부분을 그대로 식으로 나타낸 것이고, $l$번째 layer에서 두 번째 series decomposition($\mathcal S_{en}^{l, 1})$까지 끝난 값을 $\mathcal X_{en}^l = Encoder(\mathcal X_{en}^{l-1})$라고 표현한다고 보면 되고, 이 때 trend part는 따로 사용되지 않기에 “_” 로 표현했다.

Decoder

Decoder는 두 가지 파트로 구성된다:

1. Trend-cyclical components를 쌓기 위한 구조
2. Seasonal components를 위한 stacked auto-correlation mechanism

각각의 decoder layer는 inner Auto-Correlation과 encoder-decoder Auto-Correlation 을 포함하는데, 이는 예측을 개선하고 각각 과거의 seasonal information을 활용할 수 있다.

모델은 decoder에서 중간 hidden variables로부터 잠재적인 trend를 추출하여 Autoformer가 점차 trend prediction을 개선하고, auto-correlation에서 period-based 의존성을 발견하기 위한 간섭 정보를 제거할 수 있다.

Decoder layer는 총 $M$개 있고, 마지막 encoder layer로 부터 받은 latent variable $\mathcal X_{en}^N$ 을 함께 input으로 받아서 $l$번째 decoder layer를 지나온 출력값은 $X_{de}^l = Decoder(\mathcal X_{de}^{l-1}, \mathcal X_{en}^N)$로 표현된다. 더 자세한 식은 아래와 같이 표현된다.

초기 $\mathcal X_{de}$인 $\mathcal X_{de}^{0}$은 $\mathcal X_{des}$로부터 deep transform을 위해 임베딩되고, $\mathcal T_{de}^0 = \mathcal X_{det}$는 계속 축적되는 구조이다. $\mathcal W_{l, i}, i \in {1,2,3}$ 은 각 $l$번째 디코더에서 $i$번째로 추출된(빨간 박스에서 세 가지 블럭을 각각 지날때마다) trend $\mathcal T_{de}^i$에 대한 프로젝터이다.

이렇게 해서 최종 예측 값은 $\mathcal W_{\mathcal S} \times \mathcal X_{de}^M + \mathcal T_{de}^M$ 이다. 이 때, $\mathcal W_{\mathcal S}$는 마지막으로 변환된 seasonal component인 $\mathcal X_{de}^M$을 target dimension으로 투영하는 역할을 한다.

3.2. Auto-Correlation Mechanism

저자들은 auto-correlation mechanism을 제안하여 series autocorrelation을 계산하고 time delay aggregation으로 유사한 sub-series를 집계함으로써 period-based dependencies를 발견한다.

Period-based dependencies

동일한 phase position이 각 기간에서 자연스럽게 유사한 sub-processes를 제공하는 것을 관찰 가능하다. 확률 과정 이론에 영향을 받아, 저자들은 real discrete-time process {$\mathcal X_t$}에 대한 autocorrelation $\mathcal R_{\mathcal X \mathcal X}(\tau)$는 아래와 같이 구해진다.

$\mathcal R_{\mathcal X \mathcal X}(\tau)$는 $\mathcal X_t$와 $\tau$만큼 지연된 series인 $\mathcal X_{t-\tau}$ 사이의 time-delay 유사성을 보여준다. 위 figure에서 볼 수 있듯, autocorrelation $\mathcal R(\tau)$는 추정된 period length $\tau$ 에 대한 정규화되지 않은 신뢰도로 사용하여 가장 가능성이 높은 $k$개의 period length ${\tau_1, … \tau_k}$ 를 선택한다.이를 기반으로 period-based dependencies가 도출되고, 해당 autocorrelation 값에 따라 가중치가 부여된다.

Time delay aggregation

Period-based dependencies는 추정된 기간들 사이에서 sub-series를 연결한다. 저자들은 위의 time-delay aggregation block을 제안하여 선택된 time delay ${\tau_1, … \tau_k}$를 기반으로 series를 roll 할 수 있도록 한다. 이 연산은 추정된 기간의 same phase position에 있는 유사한 sub-series들을 정렬하는데, point-wise dot-product aggregation을 사용하는 self-attention 계열과는 다른 방식으로 진행되고, 마지막으로 softmax 정규화된 신뢰도로 sub-series를 집계한다.

Single head인 상황일 땐, 길이 $L$의 시계열 $\mathcal X$가 projection을 거치고 난 뒤 $\mathcal Q, \mathcal K, \mathcal V$를 얻는데, 이는 self-attention을 대체 가능하며 auto-correlation mechanism은 아래와 같다.

• 여기서 $k$는 $clogL$로 설정되고, $c$는 하이퍼파라미터이다.
• $\mathcal R_{\mathcal Q, \mathcal K}$는 series $\mathcal Q$와 $\mathcal K$의 autocorrelation 값이다.
• $Roll(\mathcal X, \tau)$ 연산은 time delay $\tau$에 따라 $\mathcal X$를 이동시키는 연산이며, 첫 번째 포지션에서 벗어난 요소들은 맨 뒤에 다시 붙게 된다.

Encoder-decoder auto-correlation에서 $\mathcal K$와 $\mathcal V$는 N번째 encoder layer의 결과인 $\mathcal X_{en}^N$이고, 이는 출력 길이 $O$로 조정되며, $\mathcal Q$는 이전 decoder block에서 가져온다.

Multi-head version에서는, $d_{model}$차원의 hidden variables와 $h$개의 헤드, $i$번째 헤드 각각의 query key value는 $\mathcal Q_i, \mathcal K_i, \mathcal V_i \in \mathbb R^{L \times \frac {d_{model}}{h}}, i \in \{1, ... , h\}$ 라고 할때, 연산 과정은 아래와 같다.

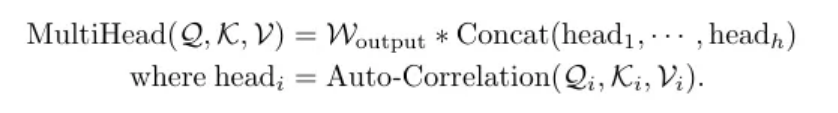
Efficient computation

Period-based dependencies는 주어진 기간에서 같은 phase position의 sub-processes를 가리키는데, 이는 기본적으로 sparse하다. 저자들은 여기서 opposite phases를 선택하는 것을 피하기 위해 가장 가능성이 높은 delay를 선택한다.

auto-correlation 계산을 위해 Fast Fourier Transforms(FFT)을 통해 위처럼 $\mathcal R_{\mathcal X \mathcal X }(\tau)$를 계산할 수 있고, 여기서 $\mathcal F^*$은 켤레 복소수 연산을 나타내고, $S_{XX}(f)$는 주파수 영역에서의 값이다.

여기서 모든 lags에 대한 auto-correlation은 FFT연산 한 번으로 계산이 되므로, 이는 $O(L log L)$의 시간 복잡도를 가진다.

Auto-Correlation vs. self-attention family

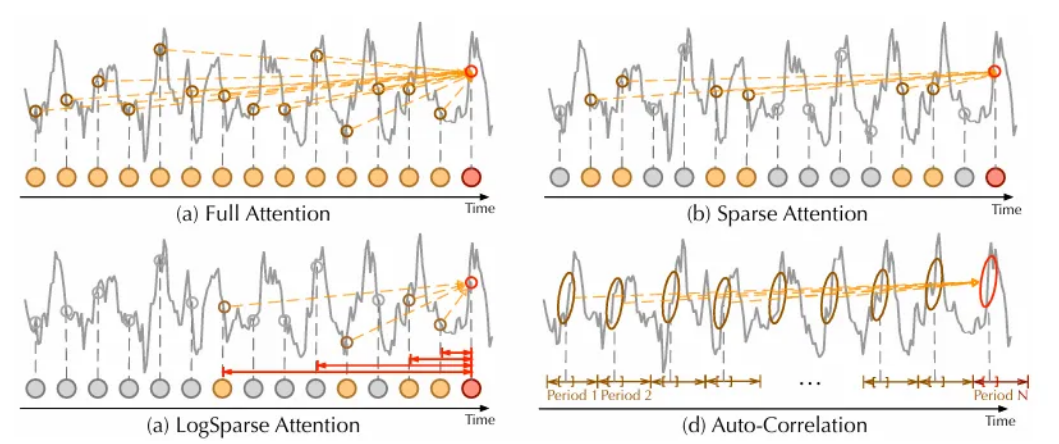
Auto-correlation은 point-wise인 self-attention 계열과 달리, series-wise한 연결이다. 정보 집계를 위해서, 저자들은 time delay block으로 기본 주기에서 유사한 sub-series들을 집계한다. 본질적인 sparsity와 sub-series-level의 representation aggregation을 사용함으로써, auto-correlation은 계산 효율적일 뿐 아니라 정보 활용도를 높일 수 있다.

---

4. Experiments

Autoformer의 성능을 5가지 주요 시계열 예측 응용 분야를 포함하는, 총 6가지 benchmark에서 평가하였다. (에너지, 교통, 경제, 날씨, 질병 등) 데이터 셋 정보와 자세한 실험 세팅, baseline 등은 논문 원문 참고

4.1. Main results

Multivariate results

Multivariate 설정에서 Autoformer는 모든 benchmark와 prediction length settings에서 SOTA를 달성하였다. 예측 길이 $O$가 증가하여도 성능이 안정적인 long-term robustness를 보인다.

Univariate results

마찬가지로 단변량 결과에 대해서도, Autoformer는 다른 모델들보다 long-term robustness가 뛰어남을 확인할 수 있다. 96→96 예측에서는 ARIMA가 더 좋은 성능을 보였지만 long-term 예측에서는 훨씬 좋지 않음을 보이는데, 이는 ARIMA가 non-stationary 경제 데이터를 처리하는 데에는 강점을 가지지만, 실제 시계열의 복잡한 temporal patten을 학습하는 데에는 한계가 있기 때문으로 생각된다.

4.2. Ablation studies

Decomposition architecture

Autoformer의 progressive decomposition architecture를 적용하면, 다른 모델 또한 성능이 향상되고, 이는 예측 길이 $O$가 증가할수록 그 효과가 더 뚜렷하게 나타난다.

이는 progressive decomposition이 다른 모델에도 일반화 될 수 있으며, 다른 dependencies learning mechanism의 학습 능력을 확장하며, 복잡한 패턴으로 인해 발생하는 distraction을 완화할 수 있음을 의미한다.

Auto-Correlation vs. self attention family

위 테이블에서 확인 가능하듯, auto-correlation은 다양한 input-$I$ predict-$O$ 설정에서 self-attention 방법들과 비교했을 때 최고의 성능을 달성했다. 또한, self-attention 기법들과 비교해서, $O$의 길이가 1440일 때 out-of-memory가 나지 않는 다는 면에서 auto-correlation이 메모리 효율적이라는 점도 증명한다.

4.3. Model Analysis

Time series decomposition

위 fig에서 확인 가능하듯, series decomposition block이 없다면 예측 모델은 증가하는 trend와 seasonal part의 peak를 제대로 포착하지 못한다.

하지만 series decomposition blocks를 추가한다면 trend-cyclical part를 잘 정제하고 집계할 수 있다. 이는 또한 seasonal part의 peaks와 troughs에 대한 학습을 가능하게 한다.

Dependencies learning

(a)에서 표시된 time delay 크기는 가장 가능성이 높은 주기를 나타내는데, 우리가 학습한 periodicity는 $Roll(\mathcal X, \tau_i)$로부터 모델이 같거나 이웃하는 phase of periods의 sub-series를 합하는 데 가이드를 줄 수 있다. 마지막 step에서 auto-correlation은 유사한 sub-series를 완전히 활용하는 반면, self-attention 기반은 그렇지 않은 것을 확인 가능하다.

Complex seasonality modeling

Autoformer가 deep representations에서 학습한 lag는 원본 시계열의 실제 seasonality를 나타낼 수 있다.

Efficiency analysis

Auto-correlation과 self-attention 기반 모델의 학습 간 실행 메모리 및 시간을 비교했을 때, auto-correlation인 빨간 선이 memory, 시간 모두 효율적인 것을 확인 가능하다.