[논문리뷰] CycleNet: Enhancing Time Series Forecasting through Modeling Periodic Patterns (NeurIPS 2024)

shyoon·2025년 2월 16일

Time Series 논문리뷰 딥러닝 머신러닝

논문리뷰

목록 보기

14/20

https://arxiv.org/abs/2310.13165

NeurIPS 2024에서 spotlight를 받은 논문

1. Introduction

Long-term time series forecasting은 날씨 예측, 교통, 에너지 관리 등 다양한 분야에서 중요한 역할을 한다.

단기 예측과는 달리 최근의 시간 정보(평균, 트렌드 등) 만으로는 학습에 충분하지 않다.

예를 들어, 사용자의 30일 후 전력 소비는 과거 며칠 동안의 소비 패턴 뿐 아니라, 더욱 긴 기간 동안의 소비 패턴과도 연관이 있다.

이런 경우, long-term dependencies는 장기 예측에 있어서 실질적인 토대를 제공하고, 이는 기존 모델들이 long-term dependencies를 갖는 features를 추출할 수 있도록 강조한다.

본 논문에서는 long-term series forecasting에서의 성능을 높이기 위해, Residual Cycle Forecasting (RCF) 기법을 제안하여 데이터 내 주기적 패턴을 명시적으로 모델링하는 방법을 탐구한다.

이전부터 Periodic information(주기적 정보)를 활용하여 모델 정확도를 향상 시키고자 한 연구는 계속해서 진행되어왔다. Autoformer, FEDformer, DLineasr 등은 전통적인 seasonal-trend decomposition(STD) 접근법으로 원본 시계열 데이터를 seasonal parts와 trend parts로 분해한 후, 이를 독립적으로 모델링하였다.

본 논문에서 제안하는 RCF 기법은 본질적으로 seasonal-trend decomposition(STD) 방법의 한 유형이고, 기존 기법과의 핵심적인 차이는 learnable recurrent cycles를 사용하여 독립적인 sequence 내 global periodic patterns를 명시적으로 모델링한다는 점에 있다.

이 RCF 기법 자체는 간단하면서도 계산 효율적이고, 예측 정확도에도 상당한 개선을 줄 수 있으며, 이에서 추가로 제안된 CycleNet은 RCF 기법을 간단한 backbone과 결합한 방식으로, 강력한 시계열 예측 성능을 보여준다.

3. CycleNet

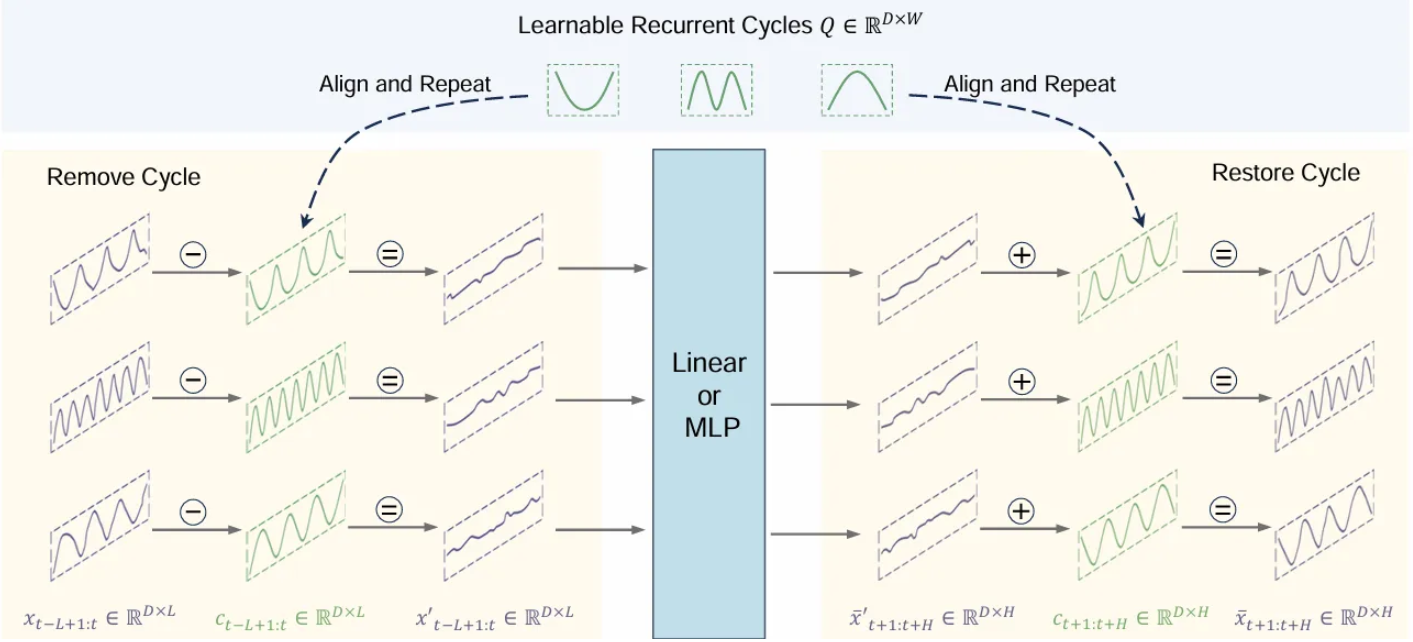
$D$ 개의 변수 혹은 채널은 가지는 시계열 $X$ 가 주어졌을 때, 시계열 예측의 목표는 과거 $L$ 개의 관측값으로 미래 $H$ step 이후의 값을 예측하는 것이다. 이는 수식으로 표현하면 $f: x_{t-L+1 : t} \in \mathbb R^{L \times D}$ → $\overline x_{t+1:t+H} \in \mathbb R^{H \times D}$ 로 표현 가능하다.

실제로, 시계열 내의 주기성은 특히 장기 예측에 있어서 필수적이다. (여러 날 ~ 몇 개월에 해당되는 96~720 steps)

저자들은 장기 예측 성능을 높이고자 Residual Cycle Forecasting(RCF) 기법과, 이를 간단한 backbone과 결합한 CycleNet architecture를 제안한다.0

3.1. Residual cycle forecasting

RCF 기법은 두 단계로 구성된다:

독립적인 채널 내에서 학습 가능한 recurrent cycles(순환 주기)를 통해 sequence의 periodic patterns(주기적 패턴)을 모델링한다. (Periodic patterns modeling)
모델링 된 주기의 residual components를 예측한다. (Residual forecasting)

Periodic patterns modeling

$D$ 개의 채널과 $W$ 의 주기 길이가 주어졌을 때, 먼저 learnable recurrent cycles인 $Q \in \mathbb R^{W \times D}$

를 0으로 초기화한다. 이러한 recurrent cycles는 채널 간 전역적으로(globally) 공유되므로, cyclic replications를 수행함으로써 sequence $X$ 와 같은 길이를 갖는 cyclic components $C$ 를 얻을 수 있다.

이 recurrent cycle $Q$ 는 backbone module과 함께 학습 시 gradient backpropagation 거치면서 learned representations를 생성하며, 이는 시퀀 스내부의 주기적 패턴을 효과적임을 드러낸다.

주기 길이 $W$ 는 데이터의 사전 특성에 의해 결정되고, 해당 데이터셋에서 가장 안정적인 주기를 사용하는 것이 좋다.

Residual forecasting

모델링된 주기의 residual components를 기반으로 예측하는 과정은 다음과 같다:

원본 input인 $x_{t-L+1:t}$ 에서 cyclic components인 $c_{t-L+1:t}$ 를 제거하여 residual components인 $x^´_{t-L+1:t}$ 를 얻는다.
$x^´_{t-L+1:t}$ 을 input으로 하여 backbone model을 통과시켜 residual components의 예측값 $\overline x^´_{t-L+1:t}$ 을 얻는다.
예측된 residual components인 $\overline x^´_{t-L+1:t}$ 을 cyclic components인 $c_{t+1:t+H}$ 와 합쳐 최종 예측값 $\overline x_{t+1:t+H}$ 를 얻는다.

여기서 cyclic components인 $C$ 는 recurrent cycle $Q$ 의 복제에서 파생된 것이기 때문에 우리가 직접적으로 앞서 언급한 sub-sequences인 $c_{t-L+1:t}$ 와 $c_{t+1:t+H}$ 를 구할 순 없고, 위 그림대로 recurrent cycle $Q$ 의 적절한 정렬(align)과 반복(repeat)을 통해 동등한 sub-sequences를 얻어야 한다.

Align

$Q$ 를 $t$ $mod$ $W$ 만큼 왼쪽으로 이동하여 $Q^{(t)}$ 를 얻는다.
여기서 $t$ $mod$ $W$ 는 현재 샘플이 $Q$ 내에서 차지하는 상대적 위치를 나타낸다.

Repeat and Concat

$Q^{(t)}$ 를 $[L / W]$ 번 반복하고, $Q^{(t)}_{0:L \ mod \ W}$ 를 연결한다.

이 align / repeat and concat 과정은 과거/미래 각각에 대해 적용된다고 보면 될 것 같다.

Backbone

원래의 예측 작업은 cyclic residual component modeling으로 변환되고, 이는 일반적인 시퀀스 모델링과 같은 방식으로 처리될 수 있다. 따라서 기존의 어떤 시계열 예측 모델도 backbone으로써 사용될 수 있고, 본 논문에서는 RCF 기법을 제안하여 시계열 예측의 성능을 높이고자 했기 때문에, 가장 기본적인 backbone인 단일 linear layer와 2개 layers로 구성된 MLP만으로도 강력한 모델을 구성할 수 있음을 보여주고자 하였다.

각 채널은 모두 동일한 backbone을 사용하며, 파라미터를 공유하는데, 이를 Channel Independent strategy라고 한다.

3.2. Instance normalization

시계열의 평균과 같은 통계적 특성은 시간이 지남에 따라 변화하기 때문에 distributional shifts가 발생한다. 이를 해결하기 위해 최근 연구에서는 instance normalization 기법을 많이 사용한다.

본 연구에서도 이를 활용하며, 저자들은 변화하는 통계량을 제거하는 방식으로 아래와 같이 정규화를 수행하였다.

$\mu$ 와 $\sigma$ 는 각각 input window의 평균과 표준편차이고, 수치적 안정을 위한 $\epsilon$ 은 매우 작은 상수로 설정된다.

3.3. Loss function

다른 주된 방법들과의 일관성 유지를 위해 CycleNet은 기본적으로 Mean Squared Error(MSE)를 loss function으로 사용한다.

4. Experiments

4.1. Setup

Datasets

ETT series, Weather, Traffic, Electricity, Solar-Energy 등 다양한 벤치마크 데이터셋에서 실험.

각각의 전처리 작업 및 샘플링 주기 등은 논문 원문 참고

Baselines

iTransformer, PathTST, Crossformer, TiDE, TimesNet, DLinear, SCINet, FEDformer, Autoformer 등 최신 SOTA 모델들과 성능 비교하였음.

4.2. Main results

CycleNet은 대부분의 데이터에서 SOTA를 달성하는데, RCF 기법을 매우 기본적인 모델(MLP, Linear)에 적용하였음에도 아주 좋은 결과를 보인다. 이는 RCF 기법의 강점을 충분히 보여준다.

예외적으로 Traffic 데이터셋에서의 성능이 iTransformer보다 떨어지는데, 저자들은 이를 Traffic 데이터셋의 시공간적 특성과 시간 지연적 특성을 iTransformer가 inter-channel 간의 관계를 충분히 모델링하지만, CycleNet은 각 채널의 temporal dependency를 독립적으로 모델링하기 때문에 해당 시나리오에서는 분리한 면이 있다고 분석한다.

4.3. Efficiency analysis

CycleNet은 학습 파라미터 수, MACs(Multiply-Accumulate Operations), 학습 시간에 있어서도 최신 SOTA 모델들에 비교하여 훨씬 효율적인 결과를 보여주었다.

4.4. Ablation study and analysis

Effectiveness of RCF

저자들은 RCF 기법의 효과를 입증하기 위해 Electricity, Traffic 데이터셋으로 몇 가지 ablation experiments를 수행하였다.

Basic linear 및 MLP backbone을 RCF와 결합하였을 때 예측 정확도가 10~20%정도로 매우 크게 향상 되었고, 이는 CycleNet의 좋은 성능에는 RCF 덕이 크다고 주장한다.
- 대체로 RCF의 유무과는 관계없이 MLP가 Linear보다 성능이 좋게 나오는데, 이는 channel-independent한 전략으로 고차원 데이터를 모델링할 때 비선형 mapping 능력이 필요하다는 점을 시사한다.
RCF는 plug-and-play 방식이므로 복잡한 딥러닝 기반의 모델에도 적용이 가능하여 타 모델에 RCF를 적용한 결과, 성능이 크게 향상되었고 이는 RCF 기법의 뛰어난 효과 및 이식성을 보여준다.
- 하지만 PatchTST 및 iTransformer에 결합하면 MAE는 감소하지만 MSE는 증가하는 경향을 보이는데, 이는 Traffic 데이터셋에서 극단값이 존재하기 때문이라고 한다.

Comparison of different STD techniques

RCF는 본질적으로 STD 기법인데, 기존 방법들은 look-back window 내에서 seasonal components를 분해했지만 RCF는 학습 데이터셋 전체에서 global periodic component를 학습한다. 이를 검증하기 위해 instance normalization을 적용하지 않은 basic linear model을 backbone으로 하여 기존 STD 기법들과 비교하였다.

RCF는 기존 STD 기법들보다 월등히 높은 성능을 보이며, 저자들은 이러한 원인을 아래와 같이 분석한다.

MOV, LD 기반 STD 기법들은 look-back window 내에서 sliding aggregation 방식으로 트렌드를 추정하기 때문에 아래와 같은 구조적인 한계를 지닌다.

Moving average의 윈도우 크기가 seasonal component의 최대 주기보다 길어야 한다. 이를 만족하지 못한다면 decomposition이 불안정할 수 있다.
시퀀스 샘플의 edge에서 동일한 크기의 moving average 시퀀스를 얻기 위해 Zero-padding이 필요한데, 이로 인해 시퀀스의 edge가 왜곡될 수 있다.
Look-back window 내에서 trend과 seasonality를 분리하는 방식은 본질적으로 제약이 없거나 약하게 제안된 linear regression과 동일하여 선형 기반 모델과 STD 기법을 결합하더라도 결과적으로 순수한 linear model과 동등한 성능을 갖게 된다.

Impact of hyperparameter $W$

$W$ 는 RCF에서 학습 가능한 reccurent cycles인 $Q$ 의 길이를 결정하는데, 원칙적으로 데이터의 maximum primary cycle length와 일치해야 시퀀스의 주기적인 패턴을 잘 모델링할 수 있다.

실험 결과를 통해 올바른 $W$ 를 설정하는 것이 성능에 큰 영향을 미치긴 하지만, 최악의 경우라도 RCF를 적용하지 않은 경우와 거의 비슷한 결과를 보였는데, 이는 $W$ 의 크기를 아무리 잘못 설정하더라도 RCF를 적용하지 않은 방법보다는 낫다는 것을 의미하기도 한다.

Visualization of the learned periodic patterns

RCF기법에서 순환 주기 $Q$ 는 초기엔 0으로 초기화되고, 학습이 진행될수록 backbone과 함께 공동 학습되어 시퀀스의 고유한 주기적인 패턴을 학습하게 된다. 아래는 서로 다른 데이터 셋 및 채널에서 학습된 주기적 패턴들을 시각화한 것이다.

예를 들어 (c)의 경우 태양광 발전의 일별(daily) 운영 패턴을, (d)의 경우엔 교통의 주별(weekly) 운영 패턴을 보여준다. 이렇게 global sequence에서 학습된 주기적인 패턴들은 예측에 있어서 중요한 보조 정보를 제공한다. 또한, 동일 데이터 셋 내에서도 각 channel마다 주기적 패턴이 다를 수도 있는데, 이를 통해 저자들은 각 channel의 주기적인 패턴을 개별적으로 모델링할 필요성이 있음을 강조한다.

Performance with varied look-back length

Look-back 길이는 활용할 수 있는 과거 정보의 풍부함을 결정한다. 해당 실험은 look back 길이에 따른 CycleNet과 기타 SOTA 모델들의 성능을 보여준다.

CycleNet을 포함한 각 모델들 모두 look-back 길이가 길어질수록 성능이 향상되는 경향을 보이는데, 이는 각 모델이 모두 long-term dependency 모델링에 강한 능력을 갖고 있음을 보여준다.

이 때 Traffic 데이터셋에서 여전히 iTransformer보다 낮은 성능을 보이는데, 변수 간 관계를 철저히 모델링해야하는 복잡한 시나리오에서는 channel-independent한 전략 및 basic backbone을 사용하는 CycleNet이 완전한 요구를 충족하긴 어려운 경우가 있다는 점을 보여준다.

5. Discussion

하지만 이렇게 long-term series forecasting에서 좋은 효과를 보이는 CycleNet도 몇 가지 논의할 만한 한계들이 존재한다.

CycleNet은 고정된 주기의 주기만 학습 가능하기에, 심전도(ECG) 데이터셋같이 주기 길이가 시간이 지나면서 변화하는 데이터에는 적합하지 않다.
CycleNet은 데이터셋 내에서 모든 채널을 동일한 주기 길이 $W$ 로 모델링하므로, 각 채널이 서로 다른 주기를 보일 경우 학습이 어려울 수 있다.
데이터셋에서 이상값이 포함될 때 악영향을 받을 수 있다.
RCF 기법은 일간/주간 주기를 모델링하는데에는 확실히 효과적이지만, 연간 주기같은 장기 의존성을 고려하는 것은 아직 도전적인 과제가 될 수 있다.

shyoon

큰 사람이 되겠어요

이전 포스트

[논문 리뷰] Autoformer: Decomposition Transformers with Auto-Correlation for Long-Term Series Forecasting (NeurIPS 2021)

다음 포스트

[논문리뷰] CycleNet: Enhancing Time Series Forecasting through Modeling Periodic Patterns (NeurIPS 2024)

논문리뷰

1. Introduction

3. CycleNet