
지금까지 살펴본 칼만 필터의 용도는
- 잡음 제거
- 측정하지 않은 상태 변수 추정
이번 장에선 칼만 필터의 센서 융합 능력을 살펴보자!
1. 관성항법 센서
칼만 필터는 특히 항공기나 인공위성의 위치와 자세를 측정하는 항법(navigation) 분야에서 절대적으로 많이 사용!
가속도계(accelerometer)와 자이로스코프(gyroscope)로 수평 자세를 찾아내는 간단한 항법 예제를 살펴보자!
📌 여기서 설명하는 내용은 자이로와 가속도계로 수평 자세를 측정하는 모든 시스템에 적용 가능
예제 11-1
가속도계와 자이로를 이용해 헬기의 수평 자세를 알아내고자 한다. 즉 헬기의 가속도와 각속도로부터, 수평면에 대한 헬기의 앞뒤 및 좌우로 기울어진 각도를 찾아내야 한다.
일반적으로 어떤 물체의 자세는 세 개의 각도, 즉 오일러 각도(Euler angle)만 알면 정확히 표현 가능!
➡ 물체의 자세를 알아낸다 = 오일러 각도를 찾는다
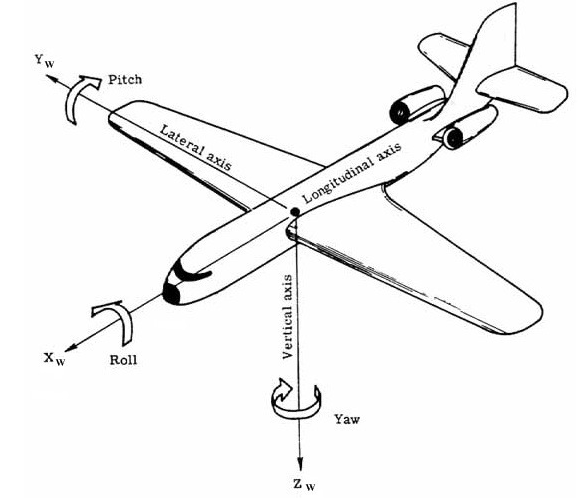
이 예제에선 수평 자세에만 관심 있으므로 roll(Φ), pitch(θ)만 찾으면 된다.
(yaw(Ψ)는 수평면에 대한 자세에 영향X)
참고)
가속도계, 자이로는 관성 좌표계에 대한 측정값을 출력한다고 해서 관성항법 센서라고 부른다.
이 관성항법 센서로 위치, 자세, 속도 등을 측정하는 방법을 관성항법이라고 한다.
✔ 여기선 자세 추정만 고려하자!
센서 융합(sensor fusion)
: 여러 센서의 출력을 모아서 더 좋은 성능을 끌어내는 기법
📌 융합용 센서를 구성할 때 상호 보완이 되는 센서끼리 묶는 것이 중요!
최종 출력에는 각 센서의 장점만 담는 것이 센서 융합의 기본 전략
예제 11-2
주파수 0.2Hz, 최대 진폭 ±30º 인 정현파로 항법 센서를 흔드는 시험을 실시했다.
시험 절차: 롤축 기동(1분) -> 정지(1분) -> 롤-피치축 기동(1분) -> 정지(1분) -> 피치축 기동(1분)
시험에서 저장한 데이터는 세 축 방향의 가속도 및 각속도, 저장 간격은 0.01초였다.
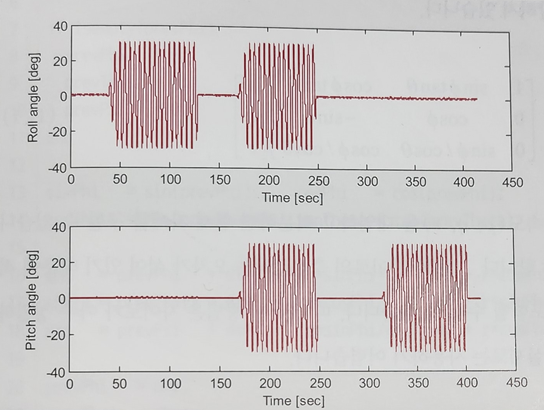
위 그림은 항법 센서에 가한 롤-피치축 진동의 궤적이다.
✔ 이 장에서 개발하는 알고리즘의 성능이 좋은지는 위 그림의 진동 궤적과 얼마나 비슷한 결과를 내는지로 판단!
2. 자이로를 이용하여 자세 측정하기
✔ 자이로와 가속도계로 수평 자세를 측정해보자!
✔ 측정 결과를 분석해서 두 센서가 왜 상호 보완이 되는지 알아보자!
✔ 칼만 필터로 두 센서를 융합해서 수평 자세를 찾아내는 기법을 살펴보고, 융합이 성공적으로 되었는지 분석해보자!
자이로로 측정한 각속도를 바로 적분하게 되면 오일러 각도를 구할 수 ❌
자이로는 오일러 각도의 변화율이 아니라, 헬기의 각속도를 측정하기 때문
➡ 자이로의 측정값을 오일러 각도의 변화율로 바꿔서 적분해야 함!
동역학 분야에서 오일러각도-각속도 관계
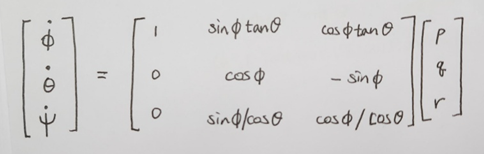
자이로에서 측정한 각속도(p,q,r)를 대입하고 적분하면 현재 자세를 구할 수 있다. (초깃값 알고 있어야 함!)
하지만 자이로의 측정값에는 오차가 포함되어 있어서 적분하여 구한 자세 또한 오차가 포함되어 있다.
➡ 이 방법은 자이로가 아주 정밀하거나 적분 시간이 짧지 않으면 실제론 사용하기 어렵❗
EulerGyro(p,q,r,dt): 오일러 각도 반환 함수
- 매개변수: p, q, r(각속도), dt(샘플링 시간)
- 반환값: 오일러 각도
function [phi, theta, psi] = EulerGyro(p,q,r,dt)
%
%
persistent prevPhi prevTheta prevPsi
if isempty(prevPhi)
prevPhi = 0;
prevTheta = 0;
prevPsi = 0;
end
sinPhi = sin(prevPhi);
cosPhi = cos(prevPhi);
cosTheta = cos(prevTheta);
tanTheta = tan(prevTheta);
phi = prevPhi + dt * (p + q*sinPhi*tanTheta + r*cosPhi*tanTheta);
theta = prevTheta + dt * (q*cosPhi - r*sinPhi);
psi = prevPsi + dt * (q*sinPhi/cosTheta + r*cosPhi/cosTheta);
prevPhi = phi;
prevTheta = theta;
prevPsi = psi;여기선 가장 단순한 적분 알고리즘을 사용했는데, 실전에선 문제의 종류에 따라 적절한 적분 방법으로 대체하면 된다.
GetGyro.m: 자이로에서 측정값을 읽어오는 함수
function [p,q,r] = GetGyro()
%
%
persistent wx wy wz
persistent k firstRun
if isempty(firstRun)
load ArsGyro % ArsGyro.mat 파일에 저장된 wx, wy, wz 변수를 반환
k = 1;
firstRun = 1;
end
p = wx(k);
q = wy(k);
r = wz(k);
k = k + 1;TestEulerGyro.m
clear all
Nsamples = 41500;
EulerSaved = zeros(Nsamples, 3);
dt = 0.01;
for k = 1:Nsamples
[p, q, r] = GetGyro();
[phi, theta, psi] = EulerGyro(p, q, r, dt); % EulerGyro 함수 호출
EulerSaved(k,:) = [phi theta psi];
end
PhiSaved = EulerSaved(:,1) * 180/pi;
ThetaSaved = EulerSaved(:,2) * 180/pi;
PsiSaved = EulerSaved(:,3) * 180/pi;
t = 0:dt:Nsamples*dt-dt;
figure
plot(t, PhiSaved)
figure
plot(t, ThetaSaved)
figure
plot(t, PsiSaved)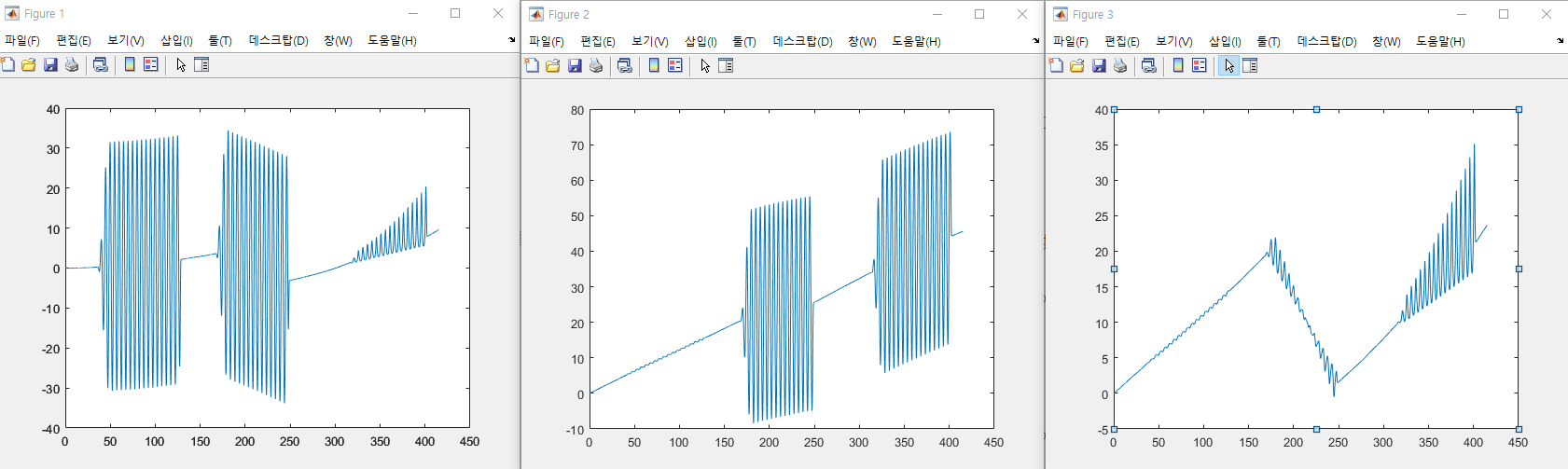
Figure 1
롤각의 변화를 보면 1~2분 사이에 ±30º 진폭으로 진동하는 움직임이 잘 보인다. 3~4분 사이에도 마찬가지.
➡ 외부에서 가한 진동이 잘 반영된 결과
하지만 누적 오차!
Figure2
피치각의 변화를 보면 0~3분 사이에는 피치축 기동이 없는데도 측정값이 점점 커지고 있다.
롤축 기동의 영향을 받아 오차가 계속 쌓여가기 때문!
각속도를 적분해서 얻은 자세는 동적 움직임(변화 패턴)을 잘 포착해내지만, 누적 오차 때문에 실제 값에서 멀어지는 특성이 있음을 알았다.
➡ 따라서 자이로는 자세각 측정보다는 자세각의 동태를 측정하는 데 더 유용
➡ 시간의 관점에서 얘기하면, 자이로는 단기간의 측정에서는 비교적 정확하지만 장시간의 변화에는 부정확한 센서
3. 가속도계를 이용하여 자세 결정하기
가속도계로 측정한 (f_x, f_y, f_z)에는 다양한 종류의 가속도가 포함되어 있다.
- 중력 가속도
- 속도의 크기나 방향이 바뀔 때 생기는 가속도
- 등등
이런 특성을 수식으로 나타내면 아래와 같다.
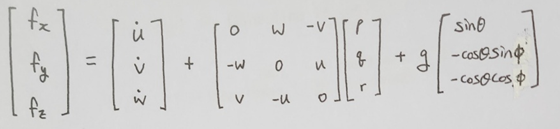
- (u, v, w): 이동 속도
- (p, q, r): 회전 각속도
- g: 중력 가속도

롤각과 피치각의 공식을 유도했다!
움직이는 속도가 충분히 느리거나 속도의 크기와 방향이 빠르게 변하지 않는다면 위의 식으로 수평 자세를 구할 수 있다.
- 보통 헬기는 대부분의 임무를 제자리 비행이나 일정 속도로 나는 도중에 수행하므로 적합
- 보행 로봇도 비슷한 조건이므로 적합
📌 위의 식으로 수평 자세를 구할 때는 이 식이 근사식이라는 사실을 꼭 기억하기!
빠른 속도로 회전하거나 속도 변화가 심하면 오차 ⬆
롤각과 피치각의 공식을 구현해보자!
EulerAccel(ax, ay, az): 롤각, 피치각 반환 함수
- 매개변수: ax, ay, az (가속도)
- 반환값: 롤각, 피치각
function [phi, theta] = EulerAccel(ax, ay, az)
g = 9.8;
theta = asin( ax / g );
phi = asin( -ay / (g * cos(theta)));GetAccel.m: 가속도를 측정해서 읽어오는 함수
: 3축 방향 가속도가 저장된 파일(ArsAccel.mat)에서 차례로 데이터를 반환
function [ax, ay, az] = GetAccel()
%
%
persistent fx fy fz
persistent k firstRun
if isempty(firstRun)
load ArsAccel
k = 1;
firstRun = 1;
end
ax = fx(k);
ay = fy(k);
az = fz(k);
k = k + 1;TestEulerAccel.m
clear all
Nsamples = 41500;
EulerSaved = zeros(Nsamples, 2);
for k = 1:Nsamples
[ax, ay, az] = GetAccel();
[phi, theta] = EulerAccel(ax, ay, az);
EulerSaved(k,:) = [phi theta];
end
PhiSaved = EulerSaved(:,1) * 180/pi;
ThetaSaved = EulerSaved(:,2) * 180/pi;
dt = 0.01;
t = 0:dt:Nsamples*dt-dt;
figure
plot(t, PhiSaved)
figure
plot(t, ThetaSaved)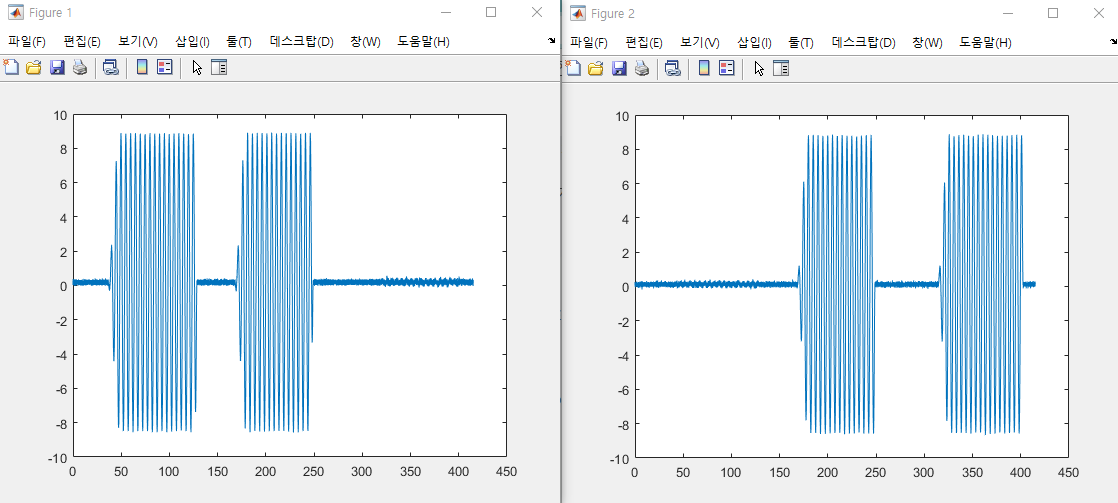
롤축 기동을 할 땐 피치축 가속도가 측정되고, 피치축 기동을 할 땐 롤축 가속도가 나타난다.
∵ 롤축 기동은 롤축 방향의 주기적인 정현파 진동이므로, 피치축이 수평면에 대해 올라가거나 내려간다. ➡ 중력 가속도와 원심력 성분 등이 피치축 가속도계에 측정된다.
(피치축 기동일 때도 마찬가지!)
가속도로 계산한 수평 자세를 살펴보자!
Figure 1: 가속도로 계산한 롤각 그래프
Figure 2: 가속도로 계산한 피치각 그래프
롤각 그래프를 보면 정현파 기동의 추이가 잘 나타나고, 자이로와 달리 가속도계로 계산한 롤각은 기동이 끝나면 다시 0º로 돌아온다.
✔ 즉 자이로와 달리 오차가 누적되지 않는다.
하지만 최댓값은 ±9º로 실제 값인 ±30º에 미치지 못한다.
✔ 오차가 상당히 커서 가속도계 단독으로 사용하긴 힘든 상태
피치각 그래프도 같은 양상!
📍 시간이 지나도 누적 오차가 없고 각이 편향되지 않지만, 오차가 너무 크다.
정리
👍장점
-
가속도계의 오차는 발산하지 않고 일정한 범위 안에 머무른다.
- 자세를 구하는 과정에서 적분을 하지 않기 때문
➡ 안정성이 높다
👎단점
-
정밀도가 떨어진다.
- 자세 계산식 (위에서 유도한 롤각과 피치각의 공식)이 가속도나 각속도가 충분히 작은 상황에서만 쓸 수 있는 근사식이기 때문
4. 센서 융합을 통해 자세 결정하기
자이로, 가속도계 두 센서가 상호 보완 관계
자이로로 구한 자세: 자세 변화 탐지👍 But, 시간이 지남에 따라 오차가 누적되어 발산하는 문제가속도계로 구한 자세: 시간이 지나도 오차가 커지지 않고 일정 범위로 제한되는 장점
➡ 단기적으로는 자이로 자세가 더 좋지만, 중장기적으로는 가속도 자세가 더 좋다.
➡ 자이로의 누적 오차 문제를 가속도계로 보정!
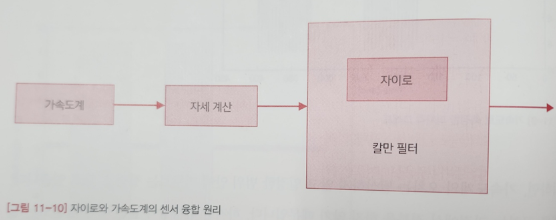
위의 그림을 보면, 가속도계로 결정한 자세가 칼만 필터의 측정값이 된다.
칼만 필터는 이 값을 자이로의 각속도를 적분하여 계산한 자세와 비교하여 오차 보정!
시스템 모델
📌 칼만 필터를 적용할 때 가장 중요한 건, 적합하고 정확한 시스템 모델을 찾아내는 것!
이번 예제도 칼만 필터 알고리즘은 동일하고, 바뀌는 건 모델이다.
➡ 어떻게 모델을 선정하는지에 집중해야 칼만 필터를 응용할 수 있음!
자이로와 가속도계의 센서 융합에 필요한 시스템 모델을 유도해보자!


센서 융합 칼만 필터 설계
EulerKalman(A,z)
- 매개변수: A(시스템 행렬), z(측정값)
- 반환값: 오일러 각도
오일러 각도와 달리 쿼터니언은 물리적인 의미가 없기 때문에, 추정 결과를 오일러각으로 변환하여 출력

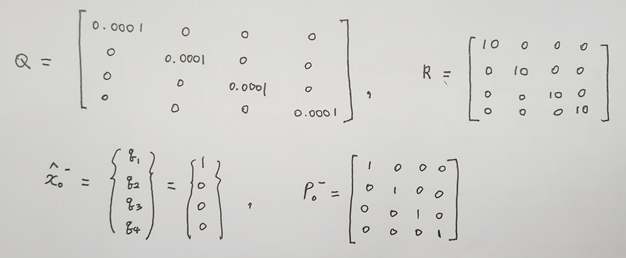
✔ 잡음의 공분산 행렬 Q와 R은 시스템의 신호 특성과 관련 있는 값이라, 이론적으로 구하기는 어렵고 실제 데이터를 분석해봐야 한다.
보통은 Q, R을 설계인자로 보고, 여러 값을 넣어 성능 변화 추이를 보면서 결정한다.
✔ 상태 변수(쿼터니언) 초깃값의 물리적인 의미는 오일러 각도가 모두 0이라는 뜻
(오일러 각도 -> 쿼터니언 변환 공식에 오일러 각도 0 넣어보면 됨)
function [phi, theta, psi] = EulerKalman(A, z)
%
%
persistent H Q R
persistent x P
persistent firstRun
if isempty(firstRun)
H = eye(4);
Q = 0.0001 * eye(4);
R = 10 * eye(4);
x = [1 0 0 0]';
P = 1 * eye(4);
end
xp = A*x;
Pp = A*P*A' + Q;
K = Pp*H'*inv(H*Pp*H' + R);
x = xp + K*(z - H*xp); % x = [q1 q2 q3 q4]
P = Pp - K*H*Pp;
% 쿼터니언 추정값을 오일러 각도로 변환
phi = atan2(2*(x(3)*x(4) + x(1)*x(2)), 1 - 2*(x(2)^2 + x(3)^2));
theta = -asin(2*(x(2)*x(4) - x(1)*x(3)));
psi = atan2(2*(x(2)*x(3) + x(1)*x(4)), 1 - 2*(x(3)^2 + x(4)^2));테스트 프로그램
EulerToQuaternion.m
function z = EulerToQuaternion(phi, theta, psi)
sinPhi = sin(phi/2);
cosPhi = cos(phi/2);
sinTheta = sin(theta/2);
cosTheta = cos(theta/2);
sinPsi = sin(psi/2);
cosPsi = cos(psi/2);
z = [ cosPhi*cosTheta*cosPsi + sinPhi*sinTheta*sinPsi;
sinPhi*cosTheta*cosPsi - cosPhi*sinTheta*sinPsi;
cosPhi*sinTheta*cosPsi + sinPhi*cosTheta*sinPsi;
cosPhi*cosTheta*sinPsi - sinPhi*sinTheta*cosPsi
];TestEulerKalman.m
clear all
Nsamples = 41500;
EulerSaved = zeros(Nsamples, 3);
dt = 0.01;
for k=1:Nsamples
[p, q, r] = GetGyro();
A = eye(4) + dt*1/2*[ 0 -p -q -r;
p 0 r -q;
q -r 0 p;
r q -p 0
];
[ax, ay, az] = GetAccel();
[phi, theta] = EulerAccel(ax, ay, az); % 오일러 각도 계산
z = EulerToQuaternion(phi, theta, 0); % 쿼터니언 각도로 변환
[phi, theta, psi] = EulerKalman(A, z);
EulerSaved(k,:) = [phi theta psi];
end
PhiSaved = EulerSaved(:, 1) * 180/pi;
ThetaSaved = EulerSaved(:, 2) * 180/pi;
PsiSaved = EulerSaved(:, 3) * 180/pi;
t = 0:dt:Nsamples*dt-dt;
figure
plot(t, PhiSaved)
figure
plot(t, ThetaSaved)
figure
plot(t, PsiSaved)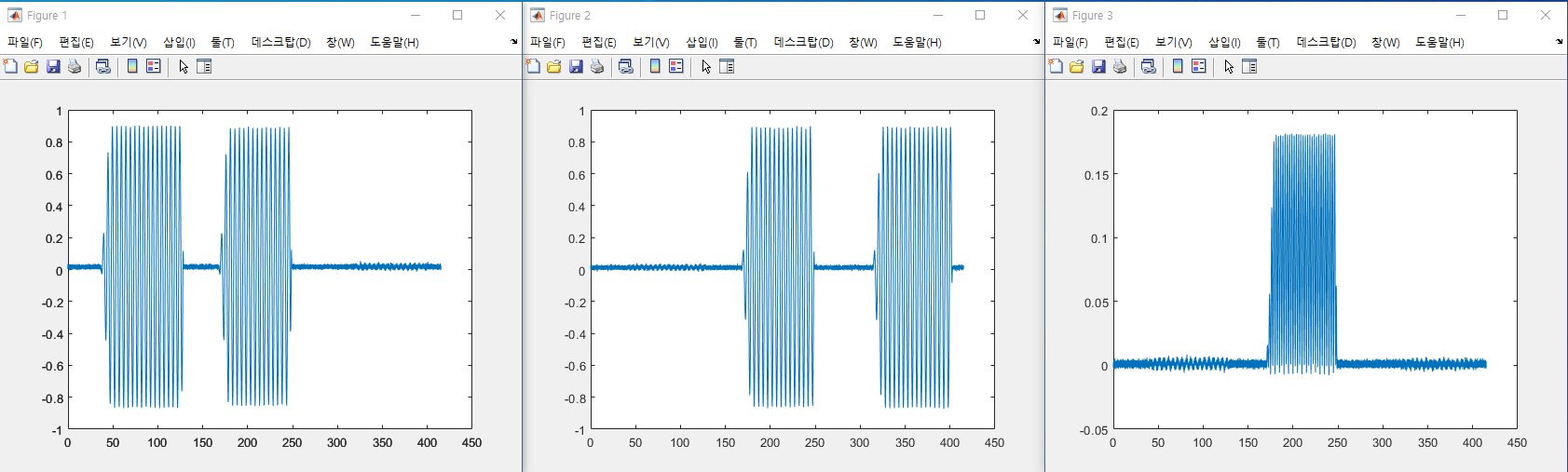
Figure 1과 Figure 2를 보면 롤각과 피치각의 궤적이 ±30º의 범위 내에서 정확하게 측정되었고, 자이로의 누적 오차도 없어졌다.
5. 가속도계를 이용하여 정밀 자세 결정하기
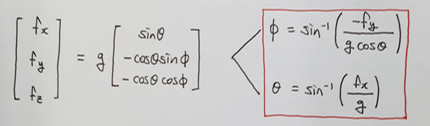
3절에서 유도했던 롤과 피치각 공식을 다르게 표현해보자.
위의 식을 (11.4) 아래 식을 (11.11)이라고 하자.
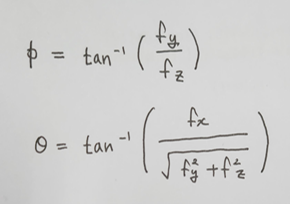
EulerAccel2(ax, ay, az)
- 매개변수: ax, ay, az (가속도)
- 반환값: 롤각, 피치각
function [phi, theta] = EulerAccel2(ax, ay, az)
theta = atan( ax / sqrt(ay^2 + az^2) );
phi = atan( ay / az );TestEulerAccel2.m
clear all
Nsamples = 41500;
EulerSaved = zeros(Nsamples, 2);
for k = 1:Nsamples
[ax, ay, az] = GetAccel();
[phi, theta] = EulerAccel2(ax, ay, az);
EulerSaved(k,:) = [phi theta];
end
PhiSaved = EulerSaved(:,1) * 180/pi;
ThetaSaved = EulerSaved(:,2) * 180/pi;
dt = 0.01;
t = 0:dt:Nsamples*dt-dt;
figure
plot(t, PhiSaved)
figure
plot(t, ThetaSaved)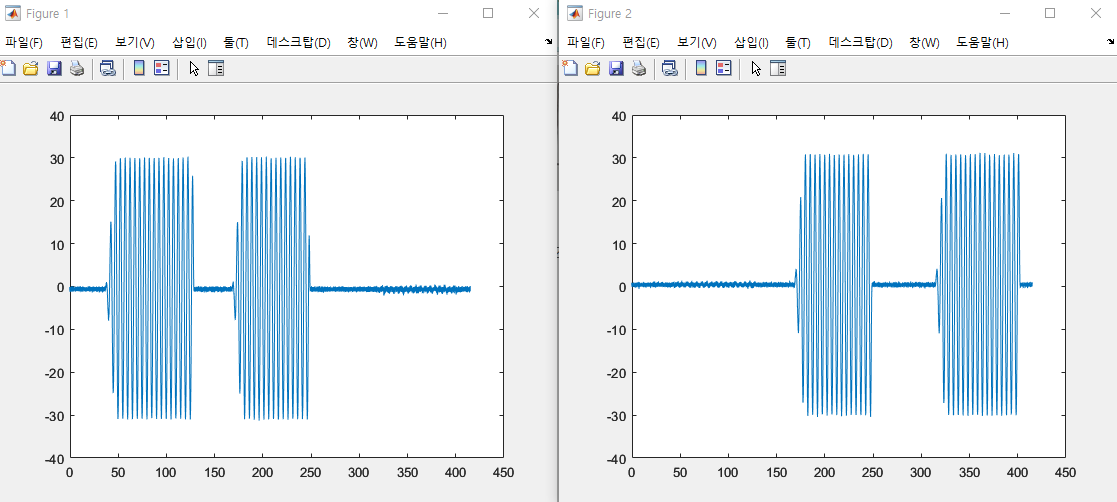
롤각과 피치각 그래프를 보면 실제 값인 ±30º에 거의 근접한 측정값을 출력한다.
가속도계로 자세각을 계산할 땐 식 (11.11)의 수식을 사용하면 식 (11.4)보다 훨씬 더 정확한 결과를 얻을 수 있다. 중력 가속도 상수가 사용되지 않는다는 장점도 있다.
식 (11.11)이 더 정밀한데 칼만 필터의 센서 융합에 식 (11.4)를 사용한 이유는 칼만 필터의 능력을 더 잘 보여주려고!
이후에 나올 예제에서도 가속도계로 자세를 측정할 때는 식 (11.4)를 사용하지만, 실전에선 식 (11.11)이 바람직!
