CNN (1)

1. CNN의 역사적 배경

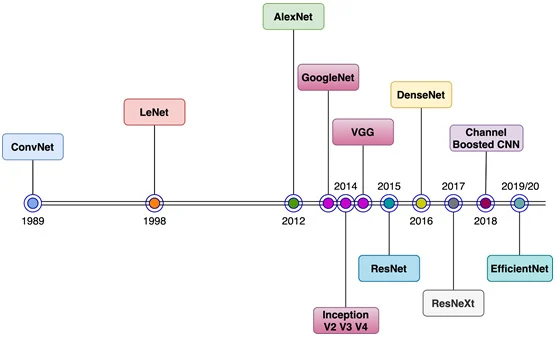
• CNN의 시작점: 1989년 이전에도 개념은 있었지만, 실질적인 시초는 LeNet

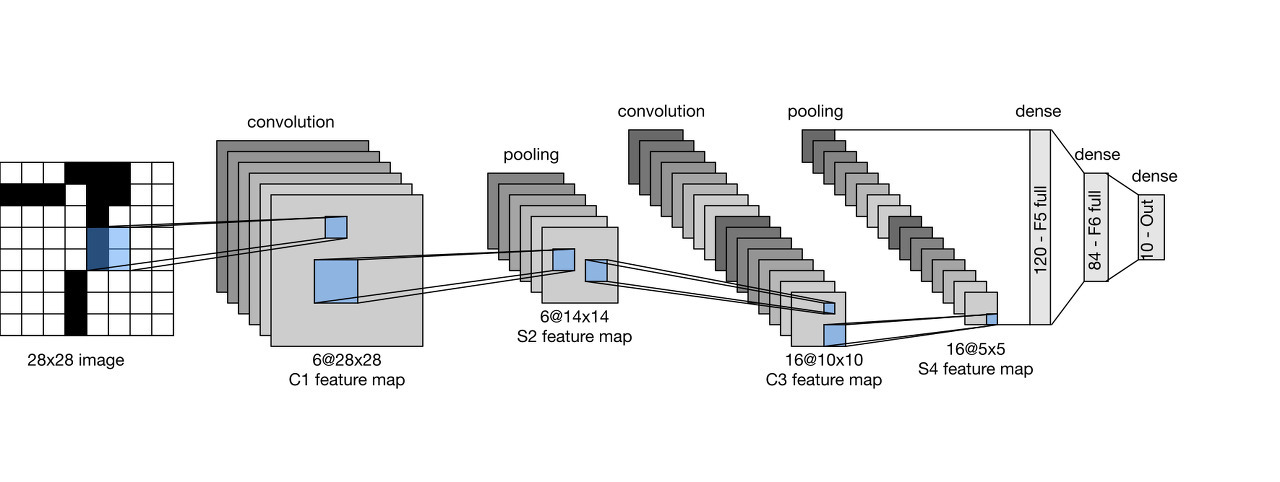
  • LeNet은 Yann LeCun이 만든 모델로 (위 그림이 LeNet),

  • $11 \times 11 \times 3$ 크기의 필터 48개로 합성곱(convolution) 연산을 수행,

  • $55 \times 55 \times 48$ 크기의 feature map 생성,

  • Max Pooling으로 차원 축소 후, Flatten → Dense Layer → Softmax 구조를 사용

2. CNN의 필요성

• 기존 Fully Connected Neural Network(FCNN)은 입력 이미지를 1차원 벡터로 Flatten해야 하므로

  • 공간적 구조(위치 정보)가 손실된다.
  • 파라미터 개수가 많아져 계산량이 커진다.

• CNN은 이미지의 2차원 구조를 그대로 유지한 채 학습하며, 합성곱(Convolution)과 풀링(Pooling)을 통해 계산량을 줄이고 더 강력한 특징 추출을 가능하게 한다.

3. CNN의 학습 방식 (Hierarchical Feature Learning)

• CNN은 층을 거치면서 단순한 특징 → 복잡한 패턴 → 고차원적 의미로 학습이 확장된다.

  • 초기 층: 모서리, 직선 등 기본 feature.
  • 중간 층: 원, 직사각형 등 복합 패턴.
  • 심화 층: 얼굴, 바퀴 등 구체적 객체의 부분.
  • 최종 층: 객체 단위 분류(고양이, 자동차 등).

• 이를 계층적 학습(Hierarchical learning)이라 한다.

4. CNN의 핵심 구성 요소

LeNet-5 구조

Input (32×32)  
 → Conv1 (6@28×28)  
 → Pool1 (6@14×14)  
 → Conv2 (16@10×10)  
 → Pool2 (16@5×5)  
 → Flatten (400차원)  
 → Dense1 (120)  
 → Dense2 (84)  
 → Dense3 (10, Softmax)

4.1 Convolution Layer

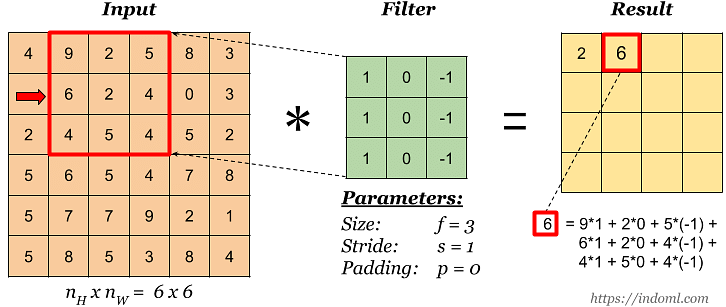
• 합성곱(Convolution): 입력 이미지와 Filter(=Kernel)를 곱해 합산하여 Feature map을 생성.
• Filter
  • 학습 가능한 파라미터(가중치).
  • 여러 개 사용 가능 → Feature map이 여러 개 생성 → 출력의 깊이(Depth) 증가.
• Stride: Filter가 이동하는 보폭 (1 → 한 칸씩, 2 → 두 칸씩).

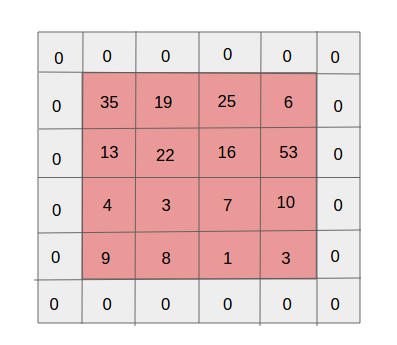
• Padding: 테두리에 픽셀(주로 0)을 추가해 출력 크기 유지.

• 예시) 입력 이미지: 숫자 “7” (28×28 픽셀, 흑백 → 채널=1)

  • Filter(=Kernel): 3×3 크기의 작은 행렬
  • Filter가 이미지의 왼쪽 위부터 오른쪽 아래까지 슬라이딩하면서 겹치는 부분을 계산
  • 즉, Convolution Layer는 이미지에서 모서리, 선, 곡선 등 기본 특징을 추출한다. 숫자 “7”이라면 → 가로 직선, 세로 직선 같은 특징이 감지됨.

4.2 Pooling Layer

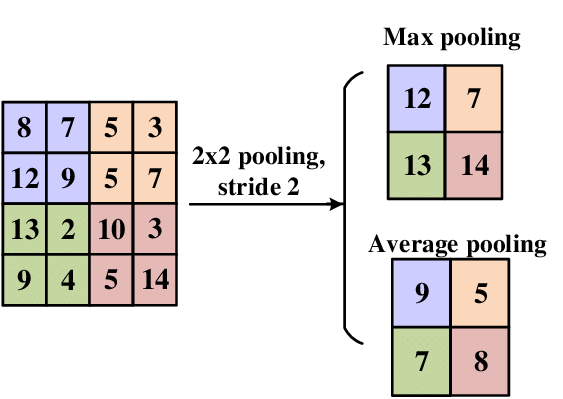
• 다운샘플링(Downsampling)으로 Feature map 크기를 줄여 계산량 감소.
• 종류
  • Max pooling: 영역 내 최대값 선택.
  • Average pooling: 영역 내 평균값 계산.
• 파라미터가 없고 단순히 크기 축소 효과.
• 예시) Convolution을 거친 Feature map이 4×4 크기로 나왔다고 가정

  Max Pooling (2×2 필터, Stride=2):
  [1 3 2 4
   5 6 7 8
   2 4 6 8
   1 1 0 0]
   
   → 2×2 영역마다 최대값만 남김. 결과:
   [6 8
   4 8]

  • 크기가 절반으로 줄어듦 → 계산량 감소
  • “7”의 특징 중 가장 강하게 감지된 부분만 남김 → 숫자의 세세한 잡음(노이즈)은 무시하고 본질적인 패턴만 유지.
  • 즉, 핵심 부분만 추출

4.3. 여러 Convolution + Pooling 반복

• 첫 번째 Convolution Layer: 모서리, 직선을 찾음.
• 두 번째 Convolution Layer: 곡선, 교차점 등을 찾음.
• Pooling이 사이사이에 들어가면서 크기를 줄이고 중요한 특징만 남김.

예: 숫자 “7” →

• Convolution1: 윗부분 가로선, 세로선 감지
• Pooling1: 불필요한 픽셀 제거
• Convolution2: “ㄱ” 모양 특징 학습
• Pooling2: 더 간단히 줄임

4.4 Fully Connected Layer

• Convolution/Pooling으로 얻은 Feature map을 Flatten(1차원 벡터) 후 분류 수행.

• CNN에서 추출된 고차원 feature를 최종적으로 활용.

  4.4.1 Flatten (1차원 벡터 변환)

  • Pooling Layer 출력을 1차원 벡터로 변환.
  • 예시: Pooling 결과가 4×4×10 (채널 포함)이라면 → Flatten → 160차원 벡터.
  • 이렇게 해야 Dense Layer(완전연결층)에 입력할 수 있음.

  4.4.2 Dense Layer (Fully Connected Layer)

  • Dense Layer(=Fully Connected Layer)는 앞에서 추출한 특징(feature)들을 종합해서 최종적인 결정을 내리는 단계
  • Convolution/Pooling → 지역적인 특징(선, 모서리, 패턴 등) 추출
  • Dense Layer → 그 특징들을 모두 모아서 “이게 어떤 숫자인지” 판단하는 데 필요한 종합적인 패턴으로 변환
    • 즉, 부분 특징을 전체 의미로 연결하는 다리 역할
  • 예시 (숫자 “7” 인식):
    • Convolution + Pooling을 거친 후 Flatten → 160차원 벡터 x 획득
      x = [0.3, 0.7, 0.1, ..., 0.5]
    • Dense Layer 연산 $z = W·x + b$ 수행
      z = [2.1, -1.5, 0.3, -0.7, 1.0, -0.5, 0.2, 3.5, 0.8, -2.0]
      • z[0] = 2.1 → “0”이라는 클래스에 대한 점수
      • z[7] = 3.5 → “7”이라는 클래스에 대한 점수 (가장 큼)
  • Dense(은닉층, ReLU 활성화) → Dense(은닉층, ReLU 활성화) → Dense(출력층, Softmax) 와 같이 여러 개의 Dense Layer(은닉층) 추가가 가능
  • 예시 (MNIST)
    • Flatten: 7×7×64 feature map → 3136차원 벡터
    • Dense Layer 1 (은닉층): 3136 → 128
      • 특징을 압축하며 “숫자 인식에 중요한 패턴”을 더 잘 조합
    • Dense Layer 2 (출력층): 128 → 10
      • 10개 숫자(0~9)에 대한 점수(logits) 출력
    • Softmax: 확률로 변환

  4.4.3 Softmax Layer (출력층)

  • 정의: Dense Layer의 출력을 확률로 변환하는 함수.
  • 수식: 각 출력 노드의 값을 exp로 변환해 양수화하고, 전체 합으로 나누어 총합이 1이 되도록 정규화
  • 역할: 모델이 출력한 값을 “이 이미지가 각 클래스일 확률”로 해석할 수 있게 만듦.
  • 예시:
    • Dense Layer 출력: z = [2.1, -1.5, 0.3, -0.7, 1.0, -0.5, 0.2, 3.5, 0.8, -2.0]
      • z[0] = 2.1 → “0”일 가능성을 나타내는 점수
      • z[1] = -1.5 → “1”일 가능성
      • …
      • z[7] = 3.5 → “7”일 가능성
    • Softmax 적용 후: softmax(z) = [0.15, 0.01, 0.03, 0.02, 0.07, 0.02, 0.03, 0.60, 0.06, 0.01]
      • 0일 확률 = 15%
      • 1일 확률 = 1%
      • 2일 확률 = 3%
      • …
      • 7일 확률 = 60% (가장 높음 → 최종 예측: “7”)
      • 8일 확률 = 6%
      • 9일 확률 = 1%