Regularization(2)

1. L1 정규화 (Lasso)

개념

• 손실 함수에 가중치들의 절댓값 합을 추가하는 방식.
  $\mathcal{L}(w) = \text{Train Loss}(w) + \alpha \sum |w_i|$
• 효과: 불필요한 가중치를 0으로 만들어버림 → 희소성(Sparsity), Feature Selection 효과.
• 학습 과정에서 중요하지 않은 가중치는 완전히 0으로 수렴.
  • 예를 들어 $[3, 0, 0.5]$처럼 일부만 살아남음.

예시

• 가중치: $[3, -4, 0.5]$
• L1 규제항: $|3| + |-4| + |0.5| = 7.5$
• 손실 함수 = $원래 Loss + \alpha \times 7.5$
• 학습 중에 모든 가중치가 조금씩 줄어듦
  • [3, -4, 0.5] → [2.5, -3.3, 0.4] … 점점 작아지면서 안정화됨.

2. L2 정규화 (Ridge)

개념

• 손실 함수에 가중치들의 제곱합을 추가.
  $\mathcal{L}(w) = \text{Train Loss}(w) + \alpha \sum w_i^2$
• 효과: 모든 가중치를 조금씩 줄임 → Weight Decay, 과적합 방지.

예시

• 가중치: $[3, -4, 0.5]$
• L2 규제항: $3^2 + (-4)^2 + 0.5^2 = 25.25$
• 손실 함수 = $원래 Loss + \alpha \times 25.25$

3. Dropout (무작위 뉴런 끄기)

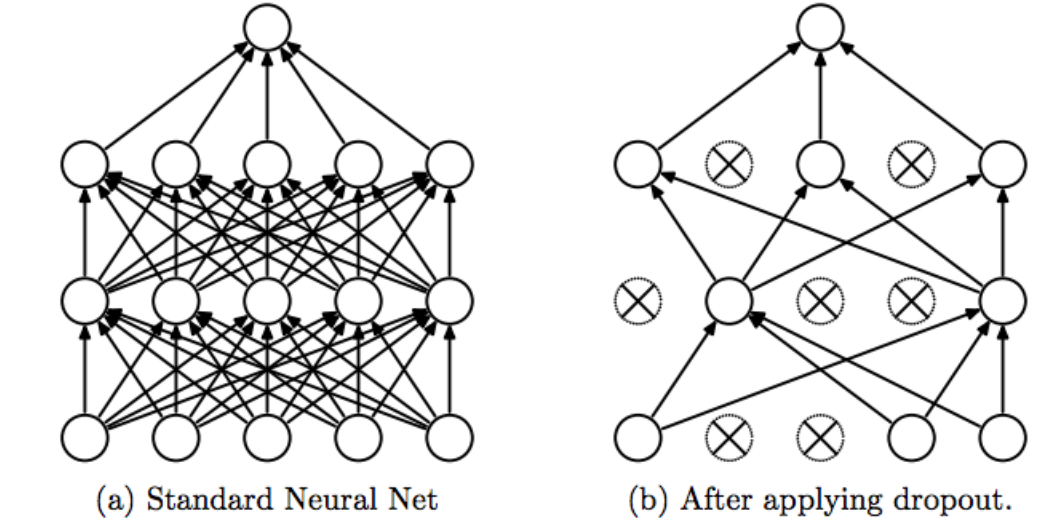
개념

• 학습 중 일부 뉴런을 무작위로 꺼버려서(=출력 0으로) 모델이 특정 뉴런에 지나치게 의존하지 않게 만드는 기법. ( 과적합 방지 )
• 매 학습 단계마다 다른 Sub-network가 학습되는 효과 → 앙상블 효과를 냄.

예시

• 은닉층에 뉴런이 4개 있다고 하자: [h1, h2, h3, h4]
• Dropout 비율 $p = 0.5$ → 학습 시 절반을 무작위로 끔.
  • 1번째 미니배치: [h1, h3]만 활성
  • 2번째 미니배치: [h2, h4]만 활성
• 이렇게 다양한 조합의 서브 네트워크가 학습됨.

4. Batch Normalization (BN)

개념

• 미니배치 단위로 각 층의 출력을 정규화(평균 0, 분산 1)하는 기법.
• 학습 시마다 데이터 분포가 변하는 문제(Internal Covariate Shift)를 완화.
• 학습 속도 개선, 초기화 민감도 감소, Gradient Vanishing 완화

예시

• 어떤 층의 출력이 [10, 20, 30, 40]이라면, 평균=25, 표준편차≈11.18

• BatchNorm 적용
  $\hat{x}_i = \frac{x_i - \mu}{\sigma}$
  → [-1.34, -0.45, 0.45, 1.34]

• 이후 학습 가능한 파라미터 $\gamma$, $\beta$를 통해 다시 스케일 조정.
  $y_i = \gamma \hat{x}_i + \beta$

5. Layer Normalization (LN)

개념

• BN은 배치 단위로 정규화하지만, LN은 한 샘플 안에서 Feature 차원 기준으로 정규화.
• 즉, 한 데이터의 모든 Feature를 평균 0, 분산 1로 변환.
• 배치 크기에 영향받지 않음 → RNN, Transformer 같은 시퀀스 모델에 주로 사용됨.

예시

• 하나의 샘플 벡터: [5, 7, 9]
• 평균 = 7, 분산 = 4
• 정규화 결과: [ (5-7)/2, (7-7)/2, (9-7)/2 ] = [-1, 0, 1 ]
• 역시 $\gamma$, $\beta$로 재조정.