신경망 (1) (Neural Network)의 기초 개념 정리

1. 신경망의 정의와 구조

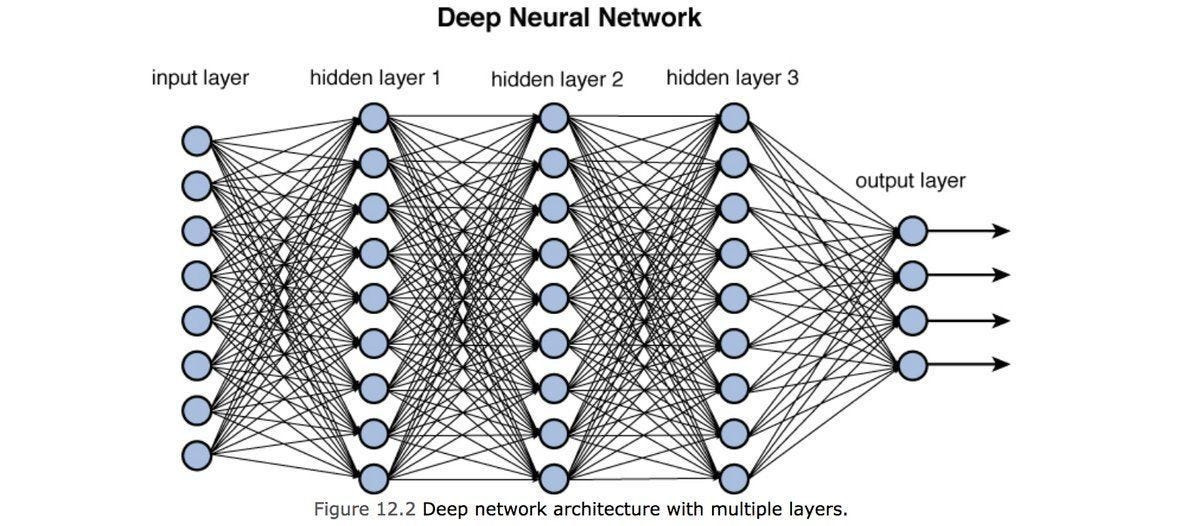
• 정의/구조: 입력층–은닉층–출력층으로 이루어진 다층 구조. 이전 층의 출력을 다음 층이 받아 점차 더 추상적인 표현(특징) 을 학습한다.

• 신경망은 오늘날 딥러닝 모델의 뼈대이고, 글은 이 기본 개념을 시작으로 CNN/RNN 등으로 확장한다.

2. AI 겨울과 부흥기

• 1차 AI 겨울 원인: 퍼셉트론의 한계(XOR 문제). 이를 깊은 신경망 + 비선형 활성화 함수 + 역전파(backpropagation) 로 극복.

• 부흥의 결정적 계기(2012): ILSVRC에서 CNN(AlexNet) 이 기존 전통 ML을 성능으로 압도 → 딥러닝 붐 본격화(Geoffrey Hinton 언급).

3. ‘합성 함수’로 보는 신경망

• 모델 표기: 신경망 전체를 함수 F로 보고, 층별 함수를 $f_1,\dots,f_n$이라 하면 $F = f_n\big(f_{n-1}(\cdots f_1(\cdot)\cdots)\big)$ 처럼 합성함수로 표현한다. 지도학습에서는 데이터 (x,y), 학습 파라미터는 w. 목표는 최적의 w 를 찾는 것(=학습)

• 학습 알고리즘: 역전파(Backpropagation)를 사용

4. 층 사이의 기본 연산 = “선형 연산”

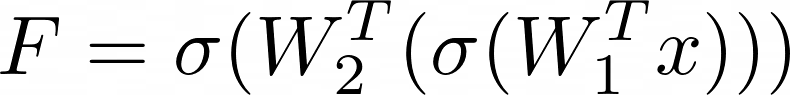
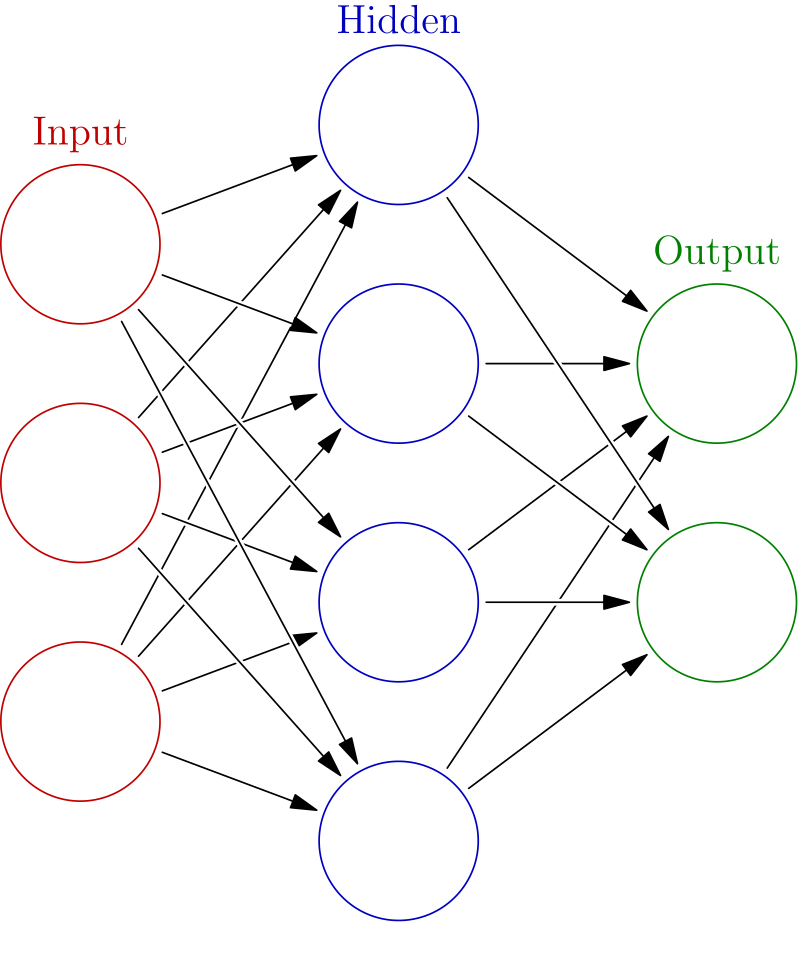
• 선형 변환: 한 층에서 대표적으로 $z = W^\top x + b$ 형태. 결국 행렬–벡터 곱 + 편향 이다.

  • $W$ : 가중치(Weight) 행렬
  • $b$ : 편향(Bias) 벡터
  • $x$ : 입력(Input) 벡터
  • $⊤$ : 가중치 행렬의 전치(transpose)

• 문제점(비선형 없음 가정): 선형 변환만 여러 층 쌓아도 전체는 하나의 큰 선형 변환 $W’ = W_n\cdots W_2 W_1$ 로 붕괴(equivalent)됨 → 표현력 한계.

5. 왜 활성화 함수(비선형)가 필요한가

• 해결책: 각 층 사이에 비선형 활성화 함수를 넣어 표현력을 확장한다. 이로써 신경망 F는 연속 조각적 선형(CPL) 특성을 갖는다(예: ReLU 기반 네트워크).

• 직관: 선형 변환만으로는 직선적 분리/근사에 갇히나, 비선형을 끼워 넣으면 복잡한 결정경계·함수도 근사 가능.

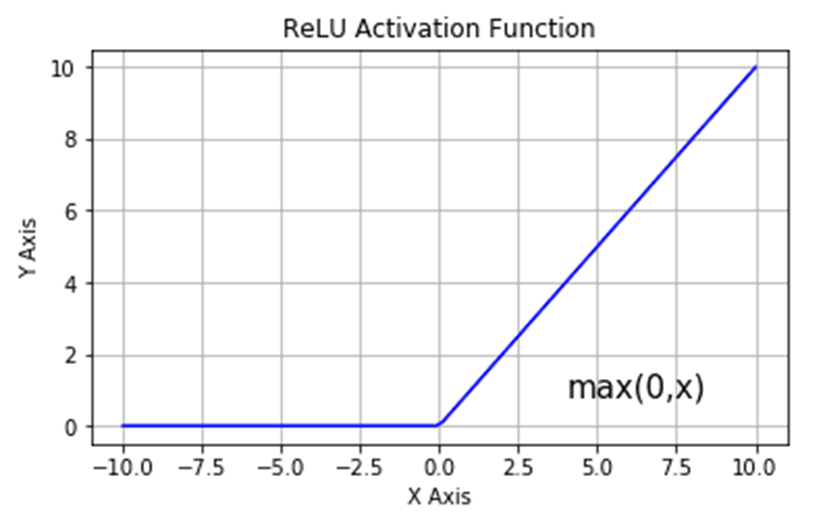
6. 활성화 함수의 대표 예시와 사용 경향

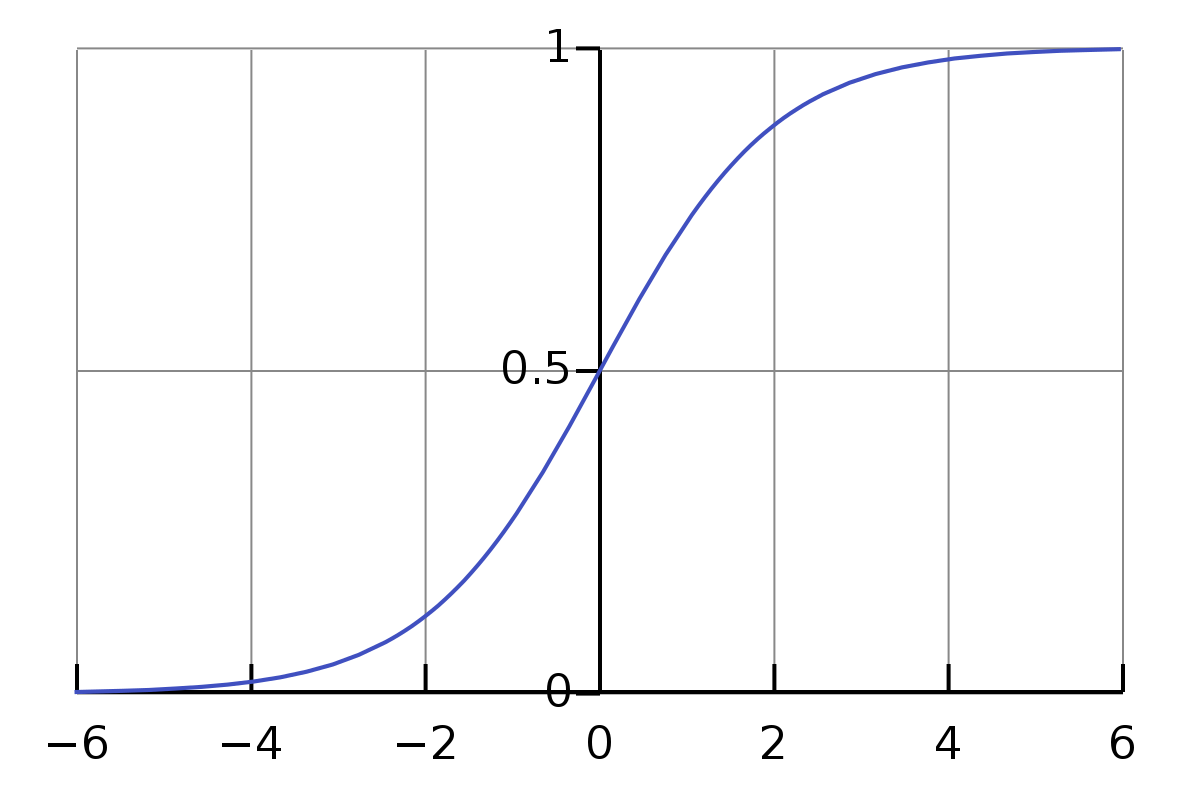
• 대표 함수: Sigmoid, Tanh, ReLU 등. 오늘날에는 ReLU 및 변형(ReLU family) 가 가장 널리 쓰임.

• 역할: 각 층의 선형 출력 z를 비선형 변환해 다음 층으로 넘기며, 네트워크가 복잡한 패턴을 학습하게 함.

요약

순전파 (Forward Propagation)

• 입력 데이터를 가중치와 편향을 포함한 선형함수와 활성화 함수를 거치면서 출력층까지 전달하는 과정

• 즉, 입력층 → 은닉층 → 출력층으로 정보를 전달하며 최종 예측값(ŷ)을 계산

• 이 과정에서는 학습 파라미터(가중치, 편향)를 업데이트하지 않고, 현재 파라미터 상태에서 단순히 출력을 만들어내는 역할을 한다.

역전파 (Backward Propagation)

• 출력값과 실제 정답값 사이의 손실 함수(loss function)를 계산합니다.

• 그다음 이 손실을 각 파라미터(가중치, 편향)에 대해 미분(Gradient 계산) 하여 오차가 어떻게 발생했는지 추적

• 연쇄법칙(Chain Rule)을 활용해 은닉층까지 거꾸로 미분을 전파한다.

• 계산된 기울기를 기반으로 경사하강법(Gradient Descent) 같은 최적화 알고리즘을 사용하여 학습 파라미터를 업데이트