우리가 많은 사람의 방대한 특징을 기록한 데이터셋이 있다고 생각을 해보자!
이 데이터셋에는 그사람이 가장 좋아하는 음식, 싫어하는 동물 등등 너무나도 다양한 feature가 있다. 하지만 우리는 이 데이터 셋으로 자원봉사에 지원할 가능성을 예측하는 모델을 만든다고 생각하자. 과연 해당모델에서 위의 예시로 들었언 두가지의 feature가 유의미한 데이터로써 모델의 성능에 도움을 줄 수 있을까? 당연히 대답은 '아니다'이다.
이런경우 우리는

무의미한 feature를 제거해야 한다 == 차원을 줄여주어야 한다 == 주성분을 추출하여야 한다.

이러한 경우 가장많이 사용되는 차원축소 알고리즘이 바로 PCA 알고리즘이다. PCA알고리즘에 대하여 알아보도록 하자.

PCA란?

PCA (Principle Component Analysis), 주성분 분석

PCA는 말 그대로 '주' 성분을 분석하는 것입니다.

분산을 보존해야한다.

저차원의 초평면에 투영을 하게 되면 차원이 줄어들게 됩니다. 그럼 어떤 초평면을 선택하면 좋을까요?

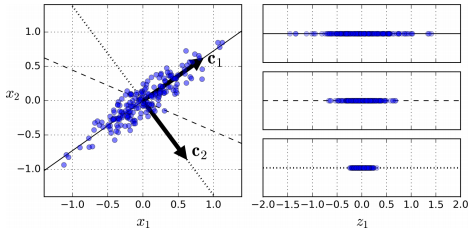
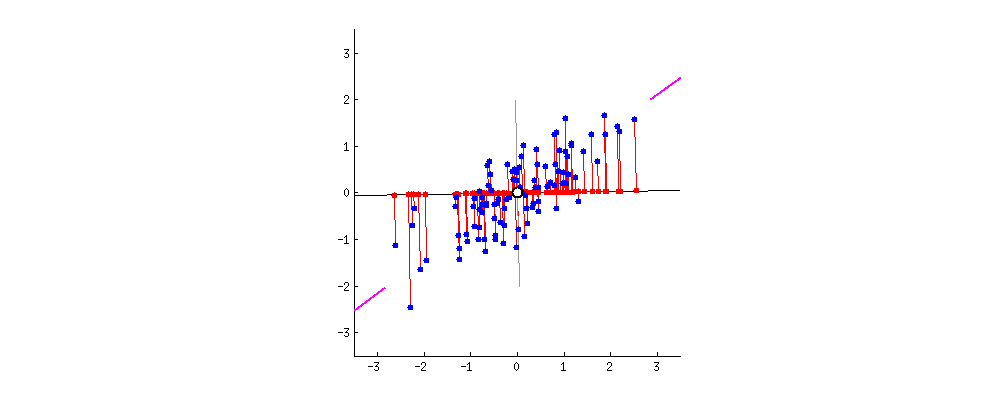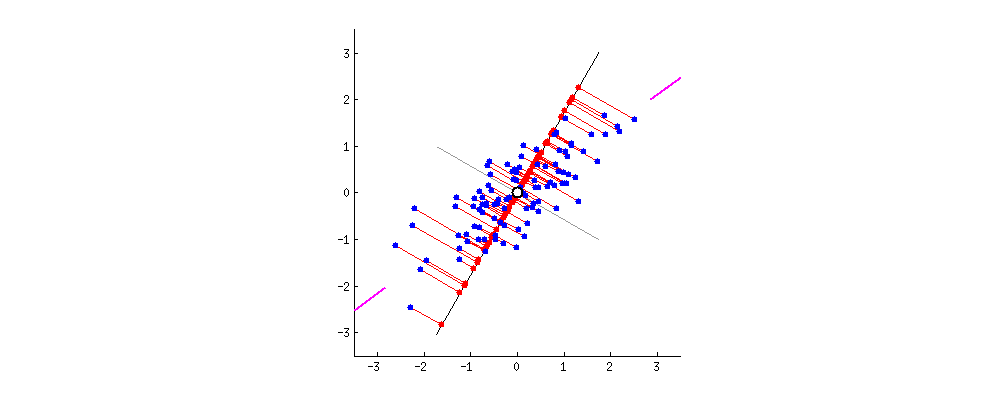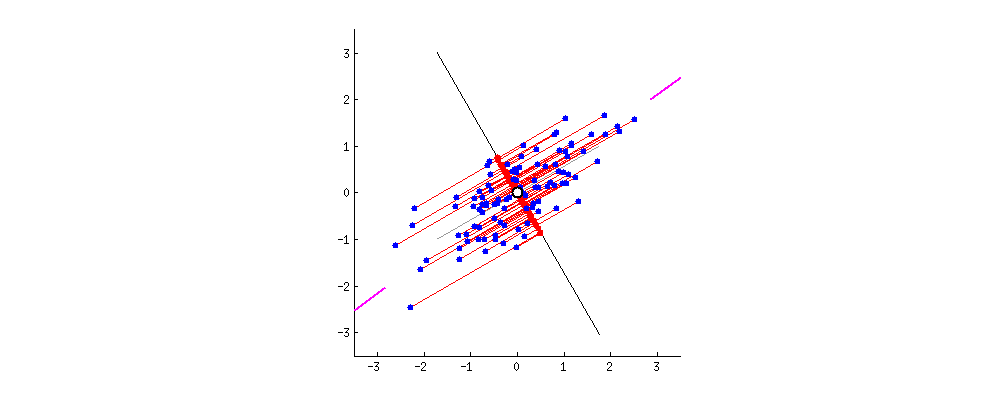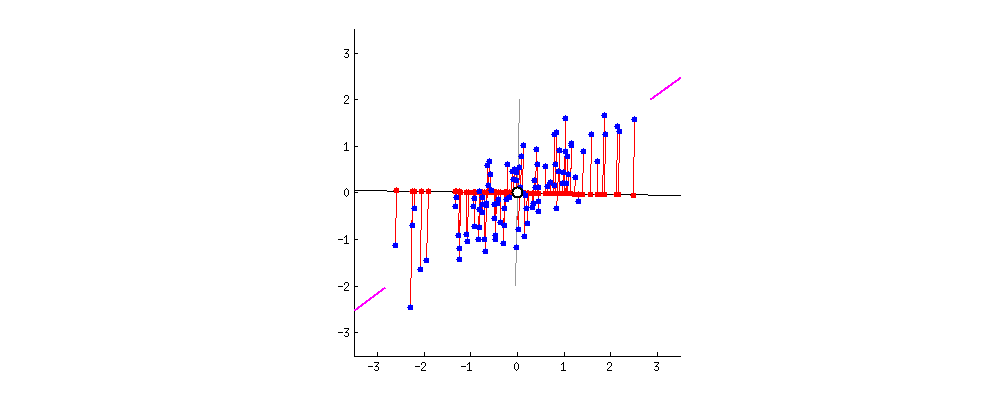
위와 같은 예시를 살펴봅시다. 간단한 2D 데이터셋이 있을 때, 세개의 축을 우리의 초평면 후보로 둡시다. 여기에서 볼 수 있는 것은 실선을 선택하는 방법이 분산을 최대로 보존하는 것이고, c2의 점선을 선택하는 것이 분산을 적게 만들어버리는 방법입니다.

다른 방향으로 투영하는 것 보다 분산을 최대로 보존할 수 있는 축을 선택하는 것이 정보를 가장 적게 손실할 수 있다고 생각할 수 있습니다. 분산이 커야 데이터들사이의 차이점이 명확해질테고, 그것이 우리의 모델을 더욱 좋은 방향으로 만들 수 있을 것이기 때문입니다.

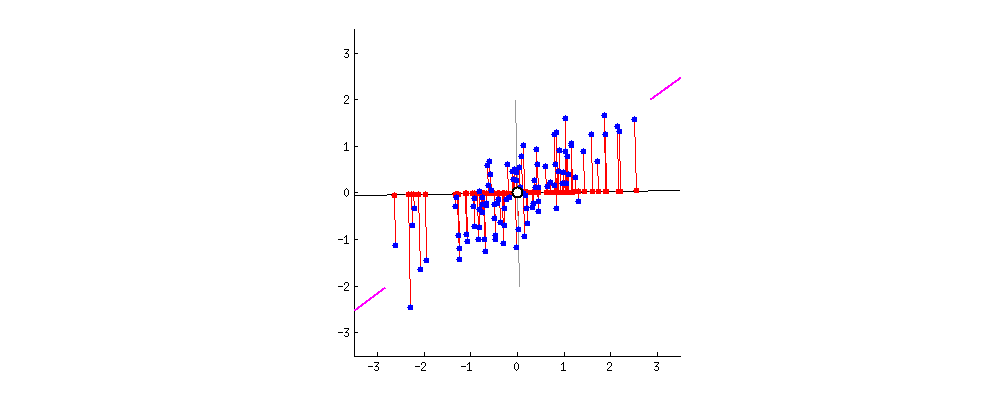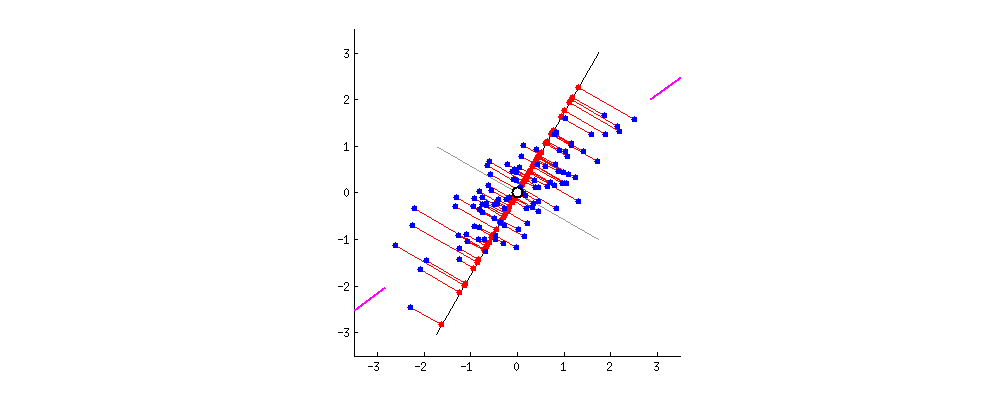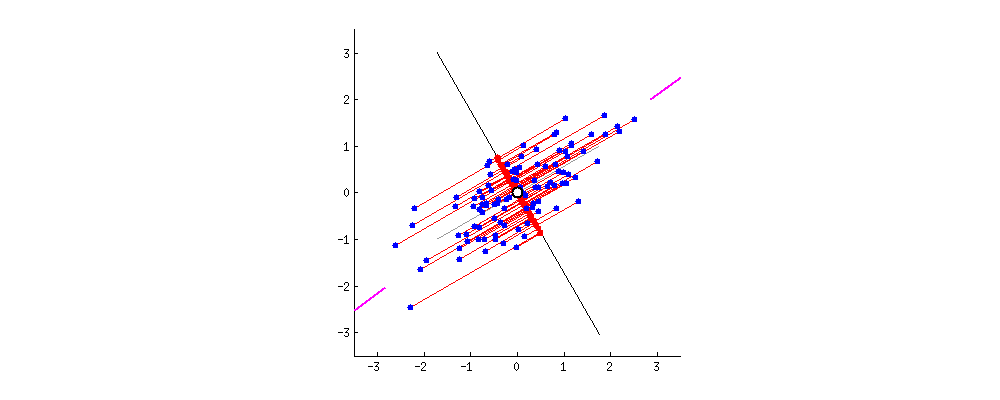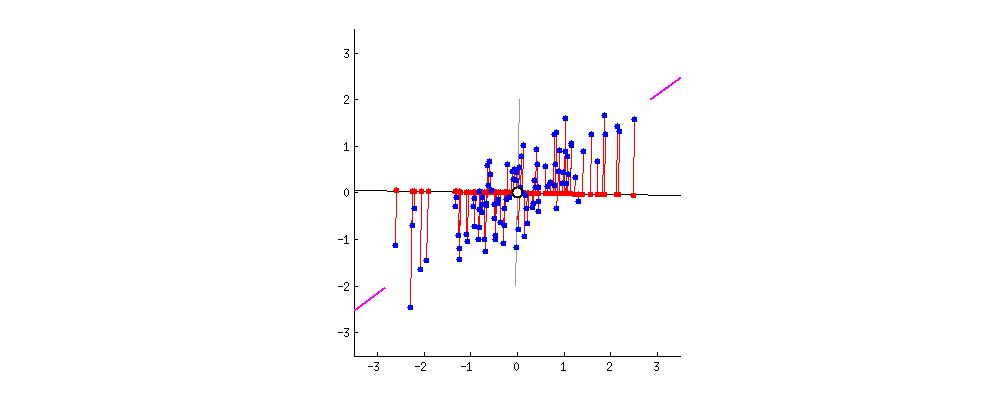
분산이 최대인 축에서 데이터와 초평면간의 거리가 가장 줄어들게 됩니다.
그래서 PCA에서는 분산이 최대인 축을 찾고, 이 첫번째 축에 직교하고 남은 분산을 최대한 보존하는 두번째 축을 찾습니다. 2D 예제에서는 선택의 여지가 없지만, 고차원의 데이터셋이라면 여러 방향의 직교하는 축을 찾을 수 있을 것입니다.

이렇게 i번째 축을 정의하는 단위 벡터를 i번째 주성분(principal component, PC)라고 합니다. 위 예제에서는 첫번째 PC는 c1이고, 두번째 PC는 c2입니다.

주성분을 찾는 법

특잇값 분해(Singular Value Decomposition, SVD)

특잇값 분해(Singular Value Decomposition, SVD)이라는 표준 행렬 분해 기술을 이용해 훈련 세트 행렬 X를 3개의 행렬의 점곱인
U
⋅
∑
⋅
V
T
로 분해할 수 있습니다. 여기서 우리가 찾고자하는 모든 주성분은 V에 담겨있습니다.

아래 파이썬 코드는 넘파잉의 svd() 함수를 사용하여 훈련 세트의 모든 주성분을 구한 후 처음 두개의 PC를 추출하는 코드입니다.

d차원으로 투영하기

주성분을 모두 추출했다면 처음 d개의 주성분으로 정의한 초평면에 투영하여 데이터셋의 차원을 d차원으로 축소할 수 있습니다. 이 초평면은 분산을 가능한 최대로 보존한 투영입니다.

초평면에 훈련 세트를 투영하기 위해서는 행렬 X와 첫 d개의 주성분을 담은(즉, V의 첫 d열로 구성된) 행렬
W
d
를 점곱하면 됩니다.

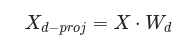
아래 파이썬 코드는 첫 두개의 주성분으로 정의된 평면에 훈련 세트를 투영합니다.

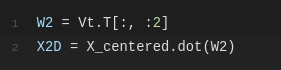
여기까지 하면 PCA 변환이 완료되었습니다!

더 쉽게 PCA를 하는 방법 - 사이킷런 이용하기

사이킷런의 PCA 모델은 앞서 한 것처럼 SVD 분해 방법을 사용하여 구현합니다. 사이킷런의 PCA모댈은 자동으로 데이터를 중앙에 맞춰줘서 별도의 가공 없이 바로 사용할 수 있습니다.