지난시간에 이어서 모델의 성능향상을 위한 '차원축소'에 관하여 다루고있는데, 오늘은 LDA에 대하여 포스팅해보려 한다. 이둘의 차이점, 공통점을 알아보며 쉽게 이해해보도록 하자!

PCA,LDA

공통점

• 차원축소 기술로 사용됨. == 유의미한 feature추출에 능이.
• 패턴분류와 머신러닝 알고리즘의 전처리 과정에 사용됨.
• 더 낮은 차원적 공간에 데이터세트를 투영하는것을 목표로함.

차이점

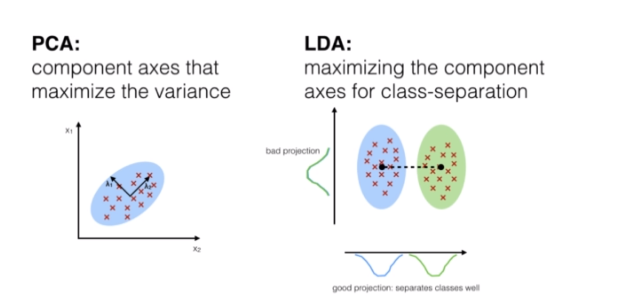
위의그림처럼

• PCA는 주성분 축들의 연관성을 검토, LDA는 클래스 분리
• PCA:비지도 알고리즘, LDA:지도 알고리즘 => 종속변수와의 연관성차이.

LDA

LDA는 아래 그림처럼 데이터를 특정 한 축에 사영(projection)한 후에 두 범주를 잘 구분할 수 있는 직선을 찾는 걸 목표로 합니다. 모델 이름에 linear라는 이름이 붙은 이유이기도 합니다.

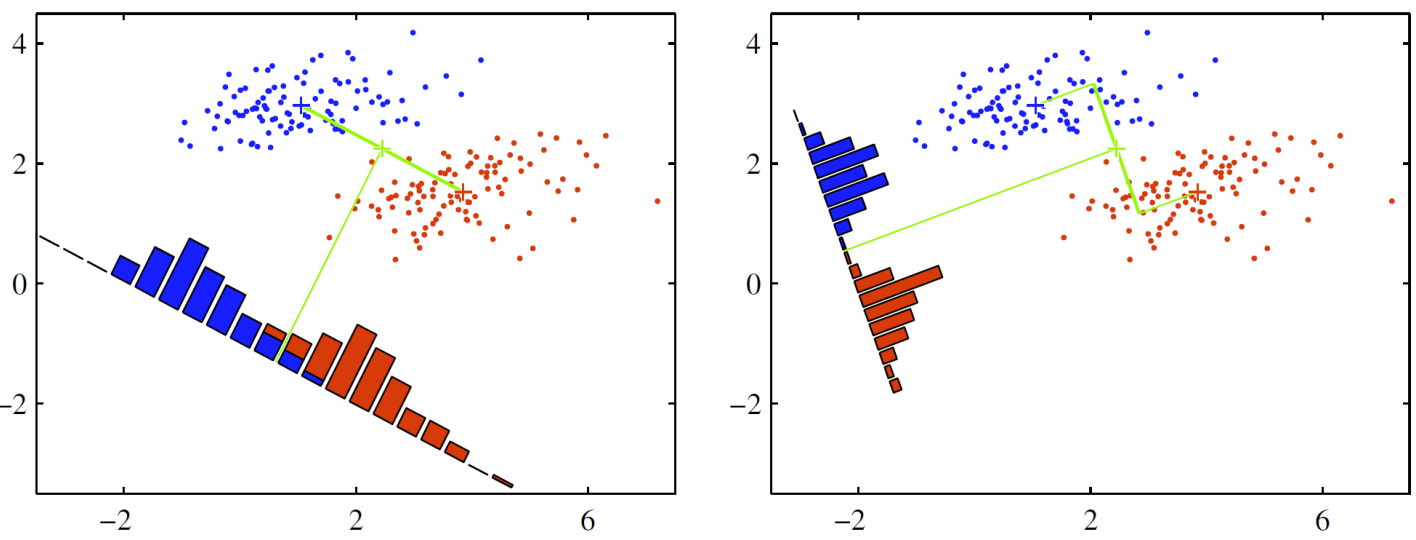
왼쪽과 오른쪽 축 가운데 분류가 더 잘 됐다고 판단할 수 있는 축은 무엇일까요? 딱 봐도 오른쪽이 좀 더 나아보입니다. 빨간색 점과 파란색 점을 분류하는 걸 목표로 했는데 왼쪽 그림에 나타난 축은 중간에 빨간색과 파란색 점이 뒤섞여 있기 때문이지요. 반대로 오른쪽 그림은 색깔이 서로 다른 점들이 섞이지 않고 비교적 뚜렷하게 구분되고 있는 점을 확인할 수 있습니다. 녹색 축을 따라서 같은 위치에 있는 점들의 빈도를 세어서 히스토그램처럼 그리면 바로 위와 같은 그림이 됩니다.

그렇다면 두 범주를 잘 구분할 수 있는 직선은 어떤 성질을 지녀야 할까요? 사영 후 두 범주의 중심(평균)이 서로 멀도록, 그 분산이 작도록 해야할 겁니다. 왼쪽 그림을 오른쪽과 비교해서 보면 왼쪽 그림은 사영 후 두 범주 중심이 가깝고, 분산은 커서 데이터가 서로 잘 분류가 안되고 있는 걸 볼 수가 있습니다. 반대로 오른쪽 그림은 사영 후 두 범주 중심이 멀고, 분산은 작아서 분류가 비교적 잘 되고 있죠. LDA는 바로 이런 직선을 찾도록 해주는 알고리즘 입니다!

LDA 간단 구현

colab바로가기