오늘 시간에는 classification에 대하여 포스팅을 할 생각이다. regression과 마찬가지로 너무나도 많이 이용되는 기법중 하나이며, 사실 regression과 classification은 서로 데이터라벨링차이에서 오는것이지 어떠한 문제에는 회귀로, 어떠한 문제에는 꼭 분류로 풀어야 하는것이 아니다. 정말정말 중요한건. "우리가 갖고있는 데이터에 모델을 맞추는것"이라는걸 다시한번 상기시키며 라벨링된 데이터가 class로 되어있을 경우(값이 연속적이지 않을경우) 유용하게 사용이가능한 분류모델(classifiacation)에 대하여 같이 공부해보는 시간이 되었으면 좋겠다.
분류모델의 종류
- 로지스틱 회귀
- KNN
- SVM
- 커널 SVM
- NB
- 의사결정 트리
- 랜덤 포레스트
로지스틱 회귀(Logistic Regression)
분류에 대하여 포스팅을 하는데 왜 회귀라는 단어가 등장한 걸까?
로지스틱 회귀(Logistic Regression)는 회귀를 사용하여 데이터가 어떤 범주에 속할 확률을 0에서 1 사이의 값으로 예측하고 그 확률에 따라 가능성이 더 높은 범주에 속하는 것으로 분류해주는 지도 학습 알고리즘이다.
예를들어 어떤 메일을 받았을 때 그것이 스팸일 확률이 0.5 이상이면 spam으로 분류하고, 확률이 0.5보다 작은 경우 ham으로 분류하는 거다. 이렇게 데이터가 2개의 범주 중 하나에 속하도록 결정하는 것을 2진 분류(binary classification)라고 한다.
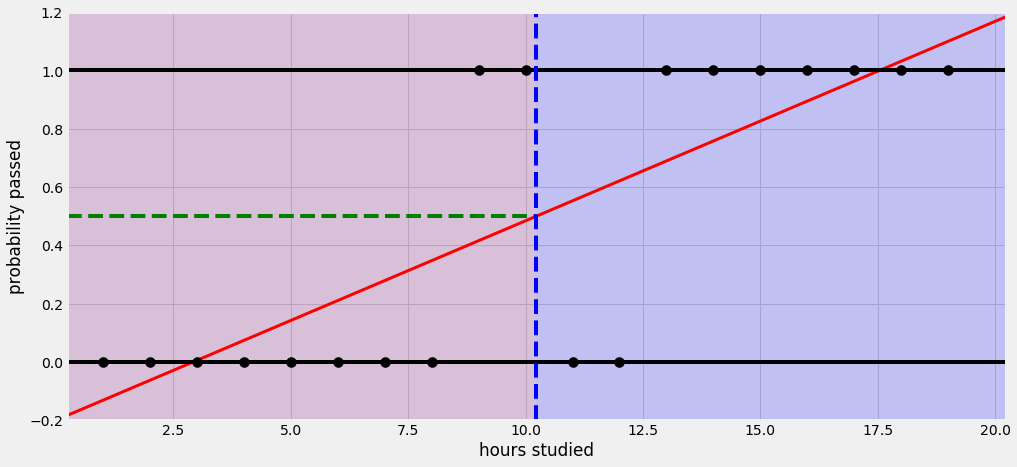
공부한 시간이 적으면 시험에 통과 못하고, 공부한 시간이 많으면 시험에 통과한다는 식으로 설명할 수 있다. 그런데 이 회귀선을 자세히 살펴보면 확률이 음과 양의 방향으로 무한대까지 뻗어 간다. 말 그대로 ‘선’이라서. 그래서 공부를 2시간도 안 하면 시험에 통과할 확률이 음수이다. 이러한 오류를 해결하기 위해 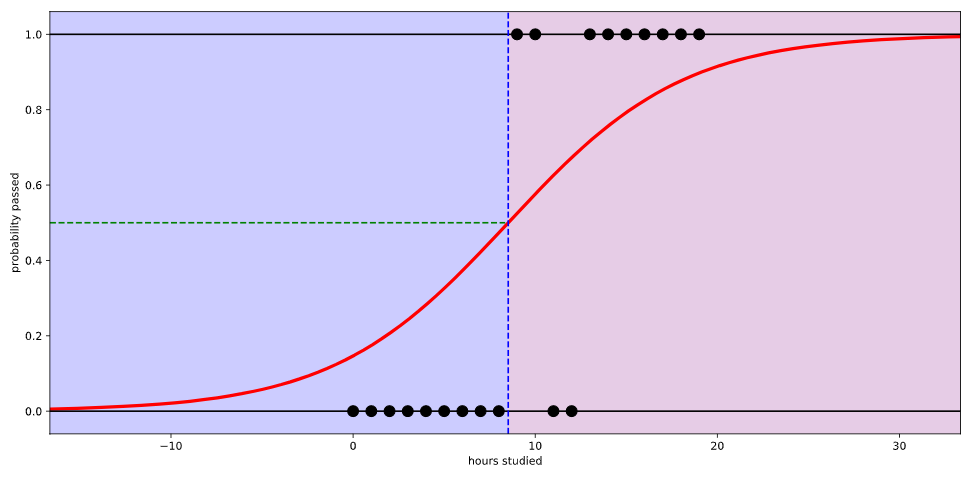
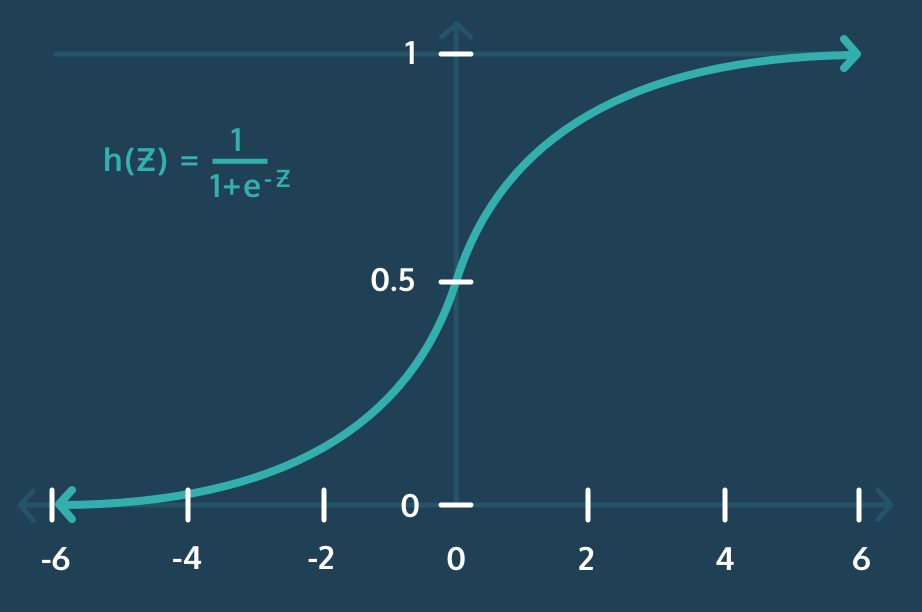
이처럼 Logistic Regression을 사용하여 0~1사이의 값으로 변환을 해주는 것이 Logistic Regression이라고 생각하면 된다.
이때 활성화 함수는 sigmoid가 사용된다.
KNN
KNN은 비슷한 특성을 가진 개체끼리 군집화하는 알고리즘입니다. 예를 들어 하얀 고양이가 새로 나타났을 때 일정 거리안에 다른 개체들의 개수(k)를 보고 자신의 위치를 결정하게하는 알고리즘이다.

단순한 알고리즘인 만큼 장단점도 확실한데 이를 정리해 보자면
kNN 장점
- 기존 분류 체계 값을 모두 검사하여 비교하므로 높은 정확도를 가짐
- 비교를 통해 가까운 상위 k개의 데이터만 활용하기 때문에 오류 데이터는 비교대상에서 제외
- 기존 데이터를 기반으로 하기 때문에 데이터에 대한 가정이 없음
kNN 단점
- 기존의 모든 데이터를 비교해야 하기 때문에 데이터가 많으면 많을 수록 처리 시간이 증가 => 느린속도
- 많은 데이터 활용을 위해 메모리를 많이 사용하게 되어 고사양의 하드웨어가 필요
SVM
서포트 벡터 머신(이하 SVM)은 결정 경계(Decision Boundary), 즉 분류를 위한 기준 선을 정의하는 모델이다. 그래서 분류되지 않은 새로운 점이 나타나면 경계의 어느 쪽에 속하는지 확인해서 분류 과제를 수행할 수 있게 된다.결국 이 결정 경계라는 걸 어떻게 정의하고 계산하는지 이해하는 게 중요하다는 뜻이다.
만약 데이터에 2개 속성(feature)만 있다면 결정 경계는 이렇게 간단한 선 형태가 될 거다.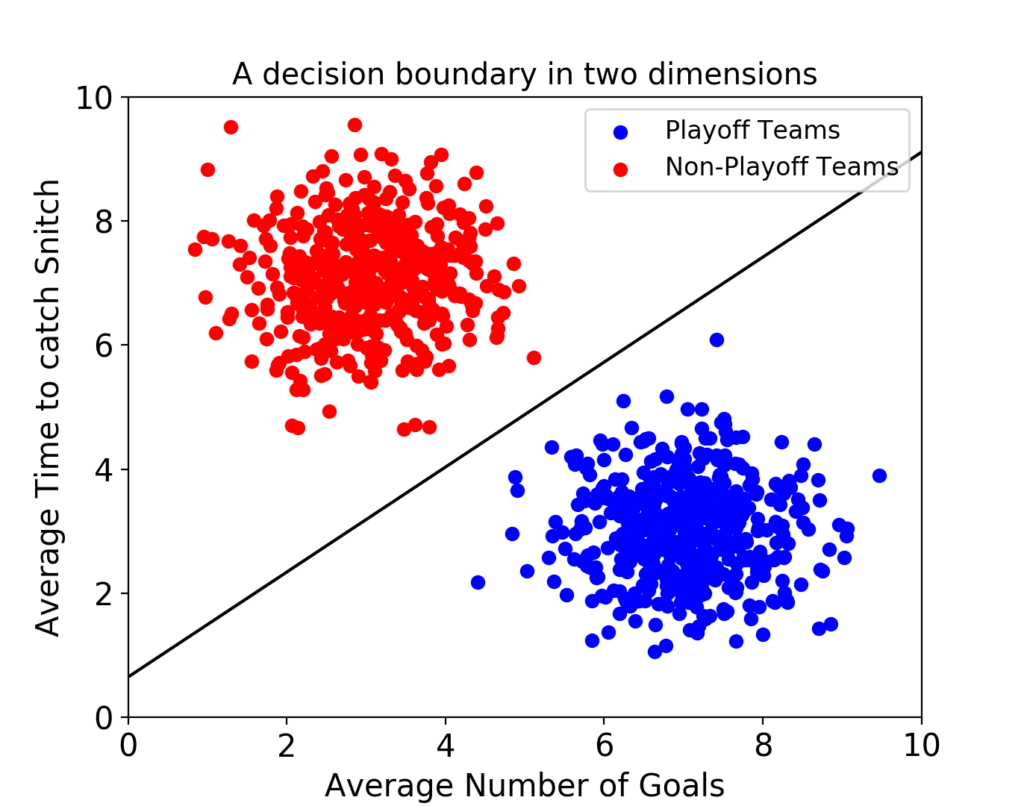
그러나 속성이 3개로 늘어난다면 이렇게 3차원으로 그려야 한다.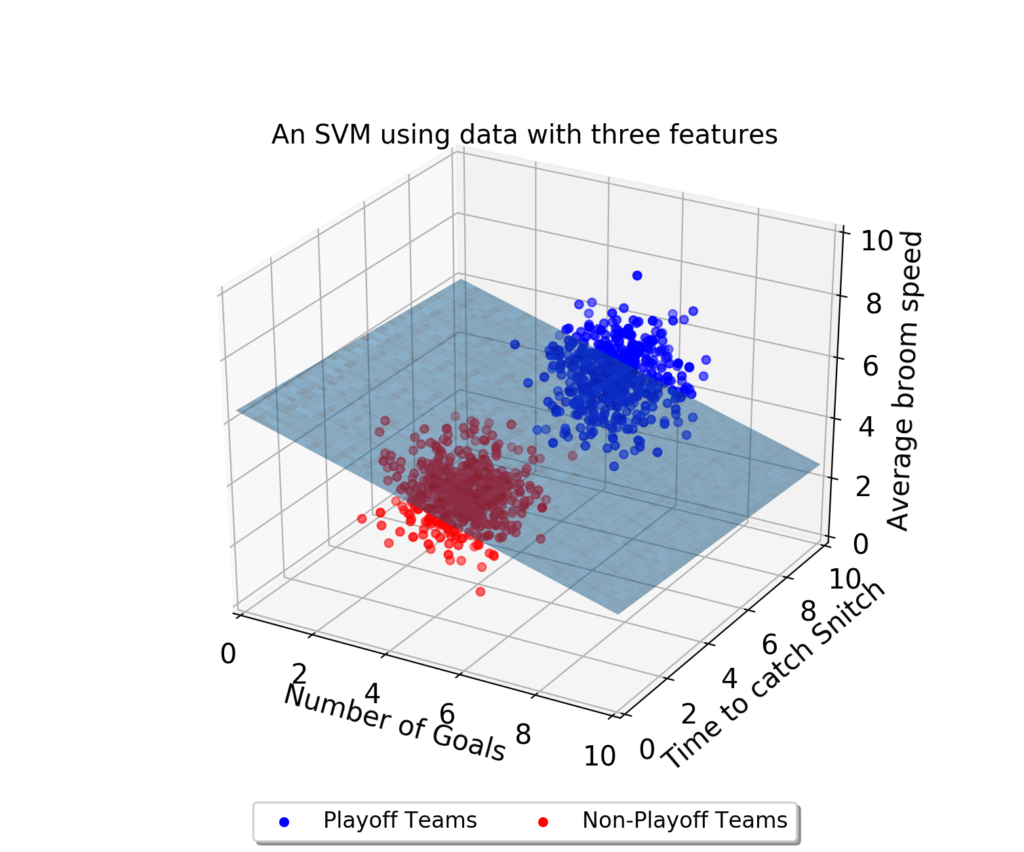
그리고 이 때의 결정 경계는 ‘선’이 아닌 ‘평면’이 된다.
우리가 이렇게 시각적으로 인지할 수 있는 범위는 딱 3차원까지다. 차원, 즉 속성의 개수가 늘어날수록 당연히 복잡해질 거다. 결정 경계도 단순한 평면이 아닌 고차원이 될 텐데 이를 “초평면(hyperplane)”이라고 부른다.
최적의 결정 경계(Decision Boundary)
결정 경계는 무수히 많이 그을 수 있을 거다. 어떤 경계가 좋은 경계일까?
일단 아래 그림들을 보자.
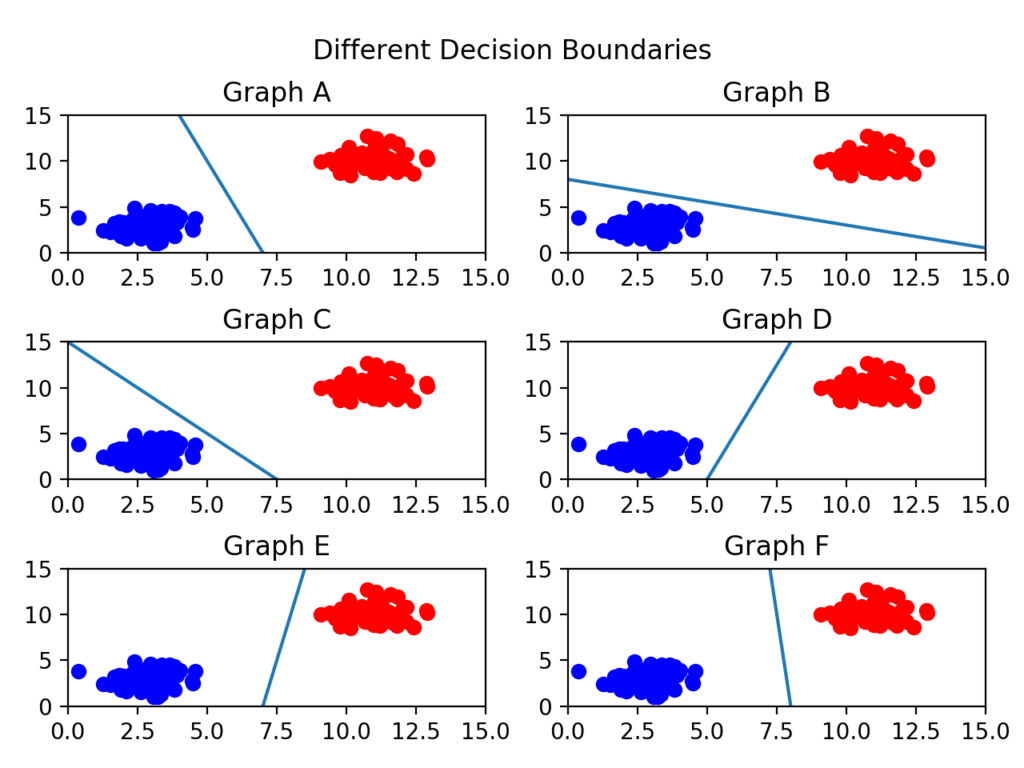
C를 보면 선이 파란색 부류와 너무 가까워서 아슬아슬해보인다.
F가 가장 적절해 보이는데 이는 두 클래스(분류) 사이에서 거리가 가장 멀기 때문이다.
이제 결정 경계는 데이터 군으로부터 최대한 멀리 떨어지는 게 좋다는 걸 알았다. 실제로 서포트 벡터 머신(Support Vector Machine)이라는 이름에서 Support Vectors는 결정 경계와 가까이 있는 데이터 포인트들을 의미한다. 이 데이터들이 경계를 정의하는 결정적인 역할을 하는 것이다.
