회귀란?

회귀는 하나의 변수가 나머지 다른 변수들과의 선형적 관계를 갖는가의 여부를 분석하는 하나의 방법이다.즉 하나의 종속변수와 독립변수 사이의 관계를 명시하는 것을 우리는 회귀라고 한다.

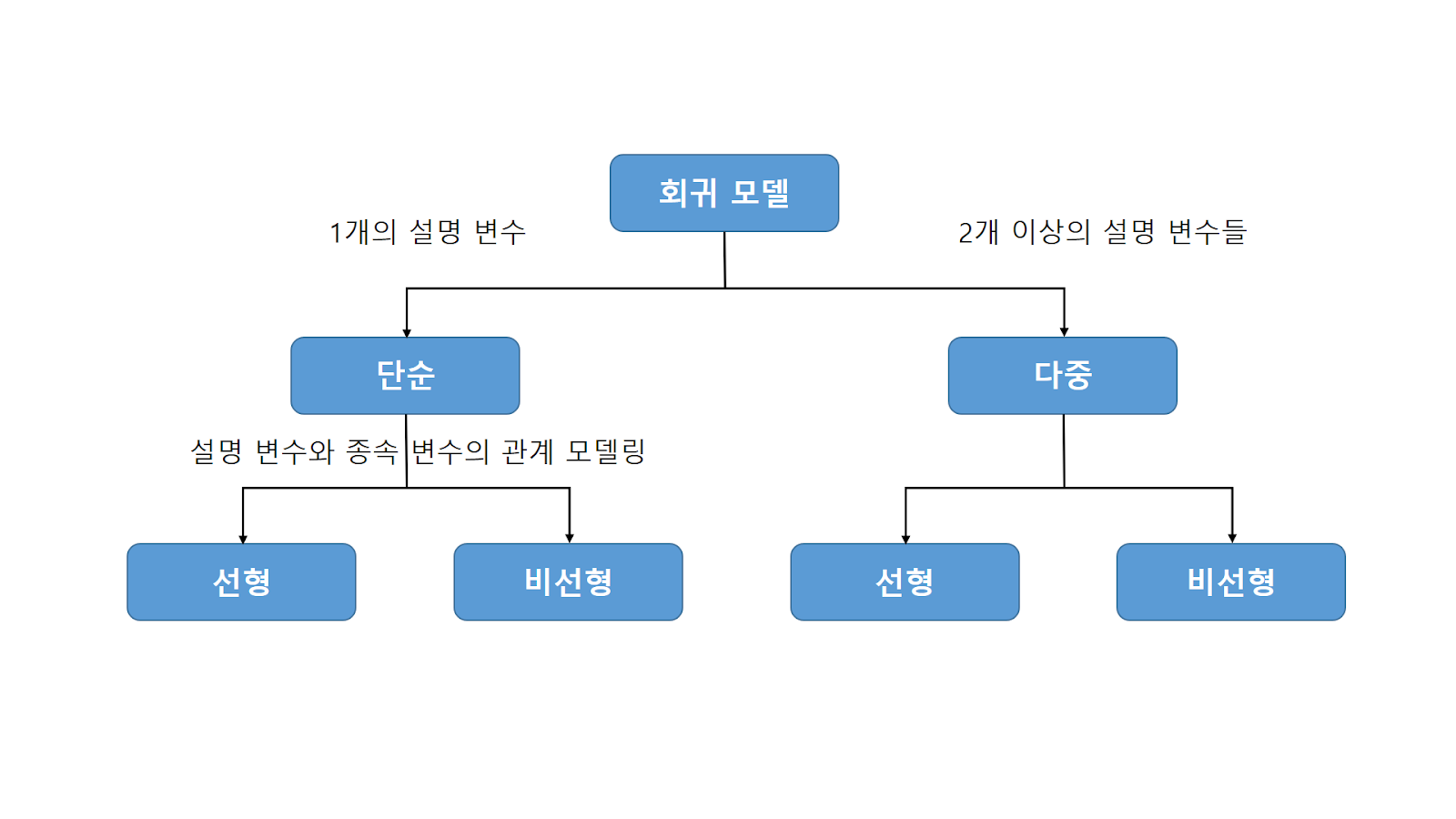
회귀모델은 위의 사진과 같이 구분을 할 수 있다. 독립변수가 1개이면 단순회귀(Simple Regression), 독립변수가 2개이상 이면 다중회귀(Multiple Regression)로 분류 할 수 있으며 각각을 또 두가지로 분류 할 수 있는데 회귀계수(기울기, x의상수값)가 선형이면 선형회귀, 비선형이면 비선형 회귀모델로 구분을 할 수 있다.

단순선형회귀

• 종속변수를 하나의 독립변수로 예측하는 것을 말합니다.

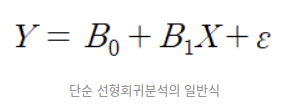
B0과 B1은 회귀계수, ε은 오차항 이라고 한다.

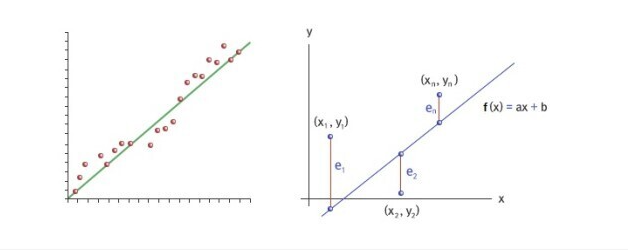
위 그림처럼, 회귀 직선은 잔차들의 제곱들의 합 RSS(Residual sum of squares)를 최소화 하는 직선을 나타냅니다.
RSS는 SSE(Sum of Squares Error)라고도 말하며, 이 값이 회귀 모델의 비용함수(Cost Function)가 됩니다.
비용함수가 최소화 하는 모델을 찾는 과정을 학습이라고 말합니다.

다중선형회귀

단순선형회귀와 같이 독립변수 X의 변화에 따른 종속변수 y의 변화를 선으로서 예측하는 기법인데, 독립변수 X가 여러개인 분석기법입니다.
독립변수 X가 여러개 = 특성(feature)이 여러개라는 뜻을 나타냅니다.

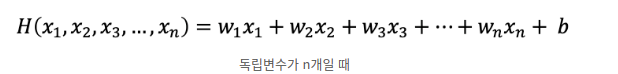
다항 회귀

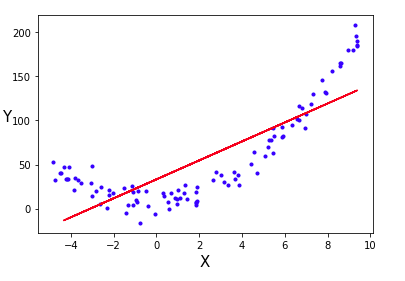
데이터셋이 선형적이라면 단순 선형회귀 역시 높은 성능을 보일 수 있겠지만, 이처럼 데이터셋이 비선형인 경우 다항회귀를 사용하는 것이 더 높은 성능을 기대할 수 있습니다.

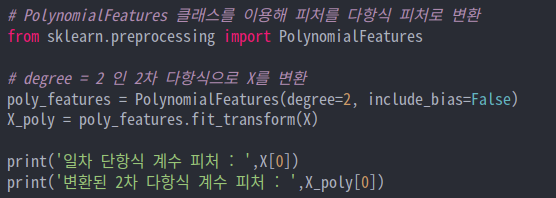
sklearn에서 제공하는 PolynomialFeatures 클래스는 dgree 파라미터를 이용해 degree에 해당하는 다항식 피쳐로 변환해 사용이 가능합니다.

SVR

Regression 에 사용되는 SVM(분류(classification), 회귀(regression), 특이점 판별(outliers detection) 에 쓰이는
지도 학습 머신 러닝 방법 중 하나이다.) 모델을 의미(분류 문제는 SVC)

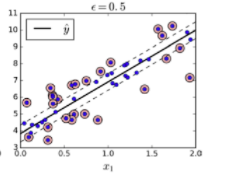
SVM 을 회귀에 적용하는 방법은, SVC 와 목표를 반대로 하는 것입니다
즉, 마진 내부에 데이터가 최대한 많이 들어가도록 학습하는 것이다.
마진의 폭은 epilson 이라는 하이퍼파라미터(절대상수)를 사용하여 조절이 가능합니다.

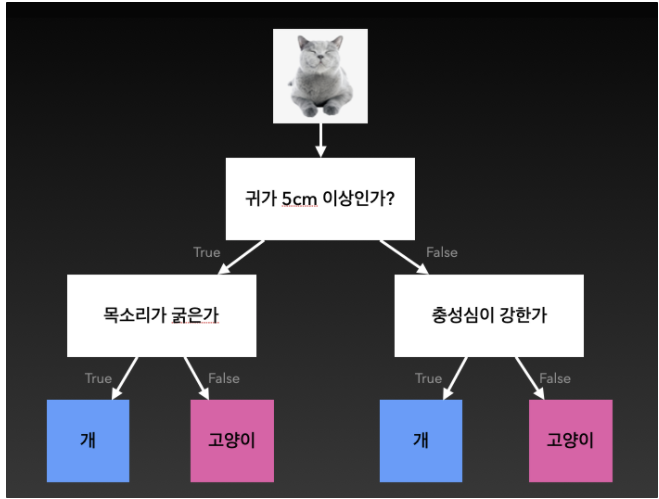
의사결정나무

의사결정나무는 회귀문제와 분류 문제에 모두 적용할 수 있습니다.
회귀문제는 회귀분석처럼 연속적인 변수에 대한 예측을 하는 것이고, 분류문제는 판변분석과 같이 어느 부류에 속하는 것인가를 예측하는 것입니다.

예를 들어보자.

우리가 자주하는 스무고개와 같은 방식으로 예, 아니오를 반복하며 추론하는 방식입니다. 생각보다 성능이 좋아 간단한 문제를 풀 때 자주 사용한다.