Nearest Neighbor Classifier

개념

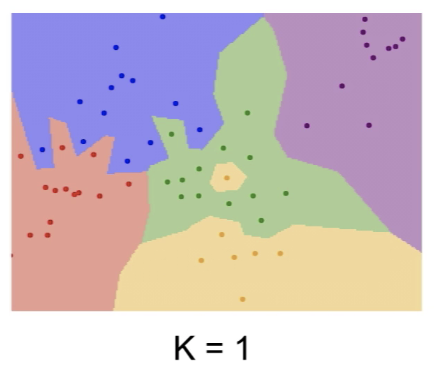
• test data point에 대해 가장 가까운 train data point를 찾고, label을 사용해 예측
• train 단계: 모든 train data-label pair를 기억
• predict 단계: test data에 대해 가장 유사한 train data의 label을 출력

def train(images, labels):
  # 모든 data와 label을 기억
  return model

def predict(model, test_images):
  # test image에 대해 가장 유사한 train image의 label 예측
  return test_labes

한계

• 학습에 $O(1)$, 예측에 $O(N)$의 시간 복잡도를 가짐.
• 학습이 오래 걸리더라도 예측이 빨라야 하는데, 그 반대임.

---

k-Nearest Neighbor Classifier

개념

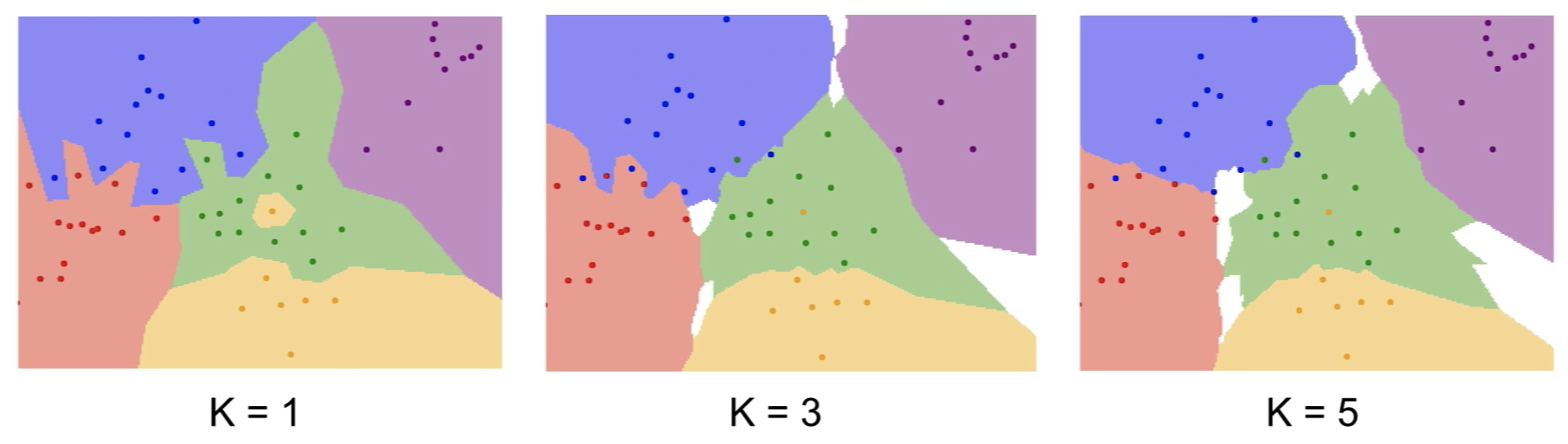
• test data point에 대해 가장 가까운 k개의 train data point를 찾고, label을 사용해 예측
• 다수결을 통해 label을 결정하므로 k는 홀수로 정함.
• k가 클수록 decision boundary가 smooth해지고 noise한 data를 잘 잡아내지만, computing time이 증가

한계

k-NN은 이미지에서 사용하지 않는데, 그 이유는 다음과 같음.

1) 거리는 정보를 제공하지 않음.

• 위 그림에서, 2~4의 변형 이미지들은 모두 원본 이미지와 동일한 L2 Distance를 가짐.
• 즉, L1, L2 거리는 이미지간의 유사도를 측정하는데 적절하지 않음.

2) 차원의 저주 (Curse of dimensionality)

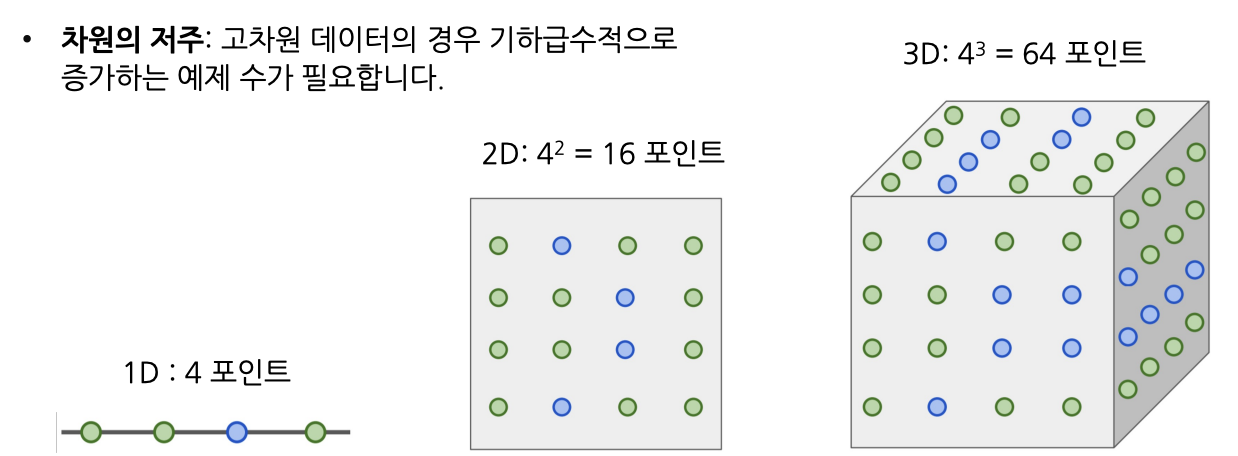
• k-NN은 train data로 공간을 적절히 잘 분할하는 작업이라 할 수 있음.
• 이를 위해선 전체 공간을 조밀하게 채울 수 있는 충분한 양의 train data가 필요함.
• 그러나, 차원이 증가함에 따라 공간을 채우기 위해 필요한 data양이 기하급수적으로 증가함.
• 고차원의 이미지인 경우, 모든 공간을 채울만큼의 이미지를 모으는 것이 현실적으로 불가함.

3) 느림.

---

Linear Classifier

개념

• 선형으로 어떠한 대상을 분류해주는 알고리즘
• 신경망(neural network)를 구성하는 가장 기본적인 요소
• 매개변수적 접근을 적용
  
  

매개변수적 접근 (Parameteric Approach)

• 모든 데이터를 저장하는 것이 아니라 파라미터 값만 저장하는 방식
• 학습 데이터의 정보를 요약해 파라미터 $W$에 모아줌.
• 예측 시 가중치 W만 필요로 하여 공간 효율성이 높음.
• 테스트 시 단일 행렬-벡터 곱 $Wx$으로 평가하여 모든 train data와 비교하는 것보다 빠름.

예시) CIFAR-10 dataset (32x32x3 pixels, 10 classes)

• $x$: 입력 이미지, $W$: 가중치
• $f(x, W) = Wx + b$ 를 통해 10개 클래스에 대한 점수를 계산
• 점수가 높다 = 해당 클래스에 속할 확률이 높다
  
  
  

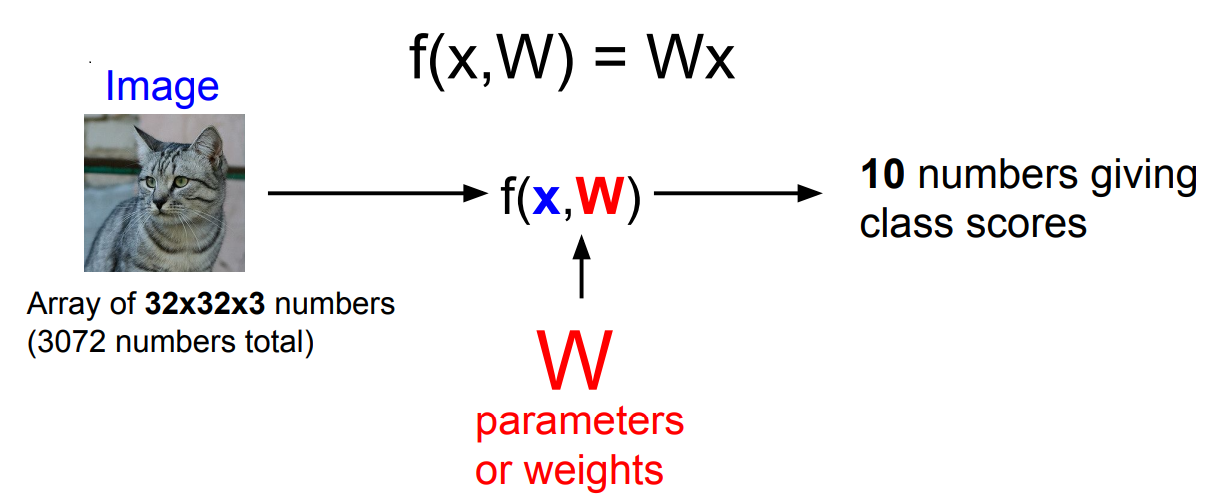
1) flatten

• 32x32x3 입력 이미지 -> (3072, 1) 열 벡터 $x$

2) weight $W$

• 열 벡터 $x$ (3072, 1)와 가중치 $W$를 내적해 10개의 숫자 (10, 1)를 얻어야 함.
• 따라서 $W$의 크기는 (10, 3072).

3) bias $b$

• dataset이 unbalance(e.g. 특정 클래스에 편중)할 경우, 특정 클래스에 우선권을 부여함.
• 입력 데이터 $x$에 무관함.
• $b$의 크기는 $f$의 크기와 같은 (10, 1).

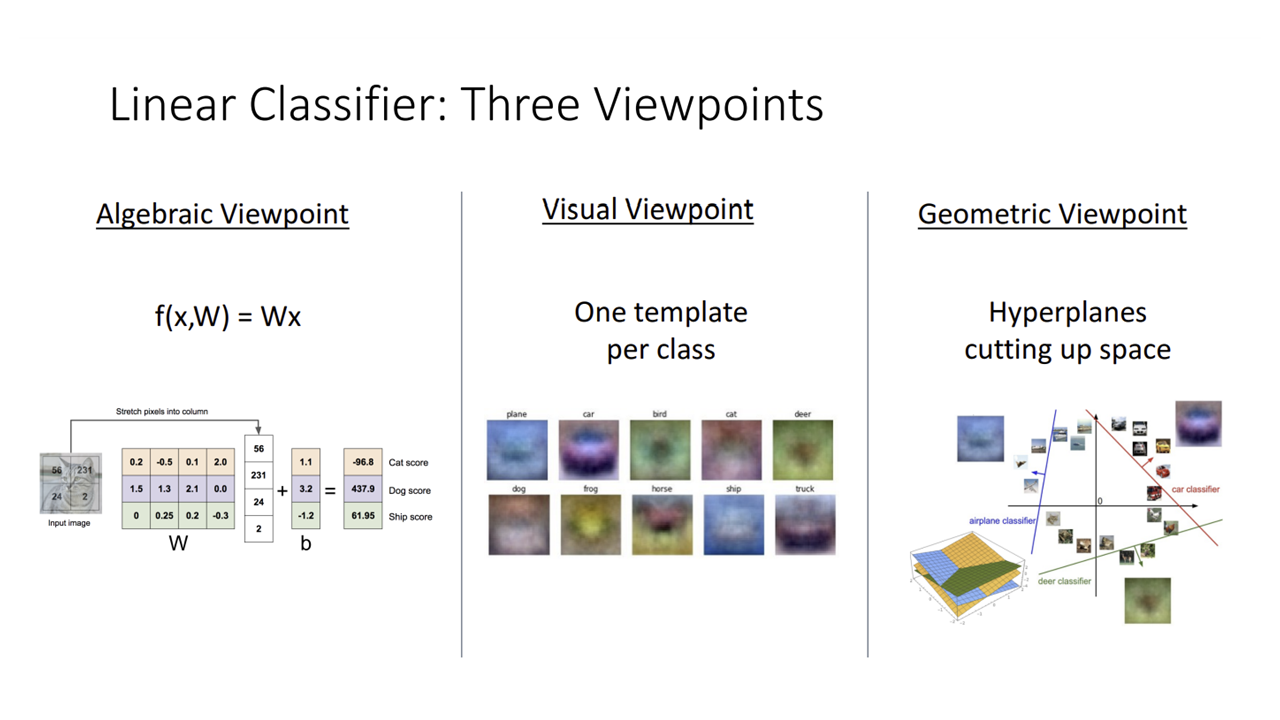
관점 1: 대수적 관점 (Algebric Viewpoint)

= Linear Classifier를 선형대수 계산으로 보는 관점

예시) 2x2 입력 이미지를 3개의 class로 분류하는 상황

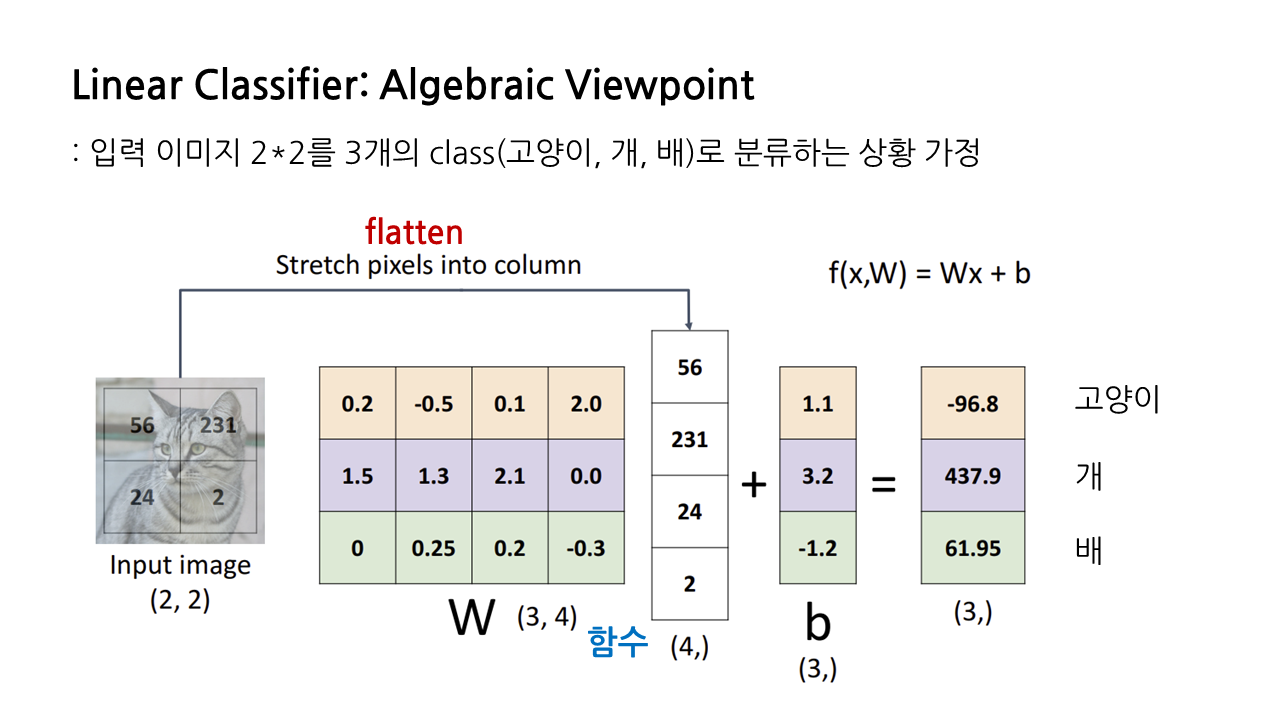
1) flatten

• 2x2 입력 이미지 -> (4, 1) 열 벡터 $x$

2) weight $W$

• 분류하고자 하는 class의 수가 3개, 열 벡터의 크기가 4
  -> $W$의 크기는 (3, 4).

3) 계산

• 행렬 $W$와 열 벡터 $x$ 사이에서 내적 연산을 수행한 뒤, $b$를 더해줌.
• 이렇게 구한 $f$는 각 class에 대한 점수를 나타냄.

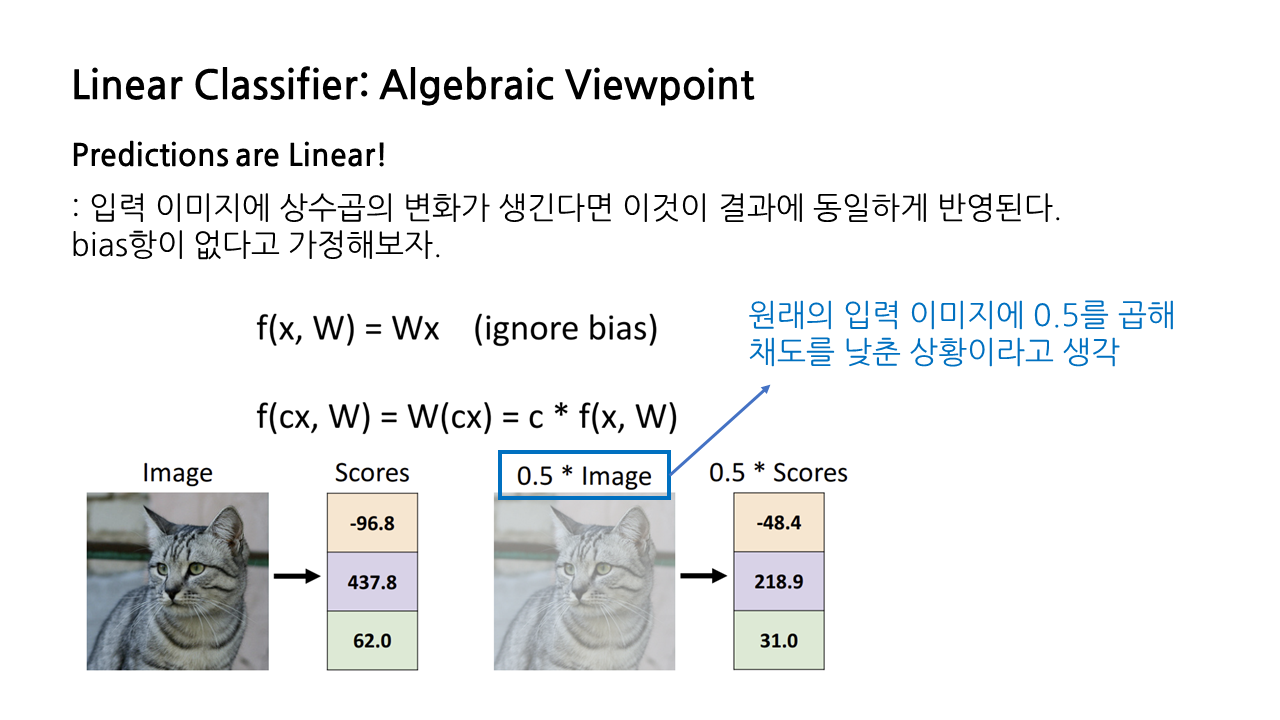
• 입력 이미지에 상수곱 $c$의 변화가 생겼을 때, 결과에도 선형적으로 반영됨.
• 예컨대 입력 이미지에 0.5를 곱해 채도를 낮추면, 점수 $f$도 0.5배가 됨.

관점 2: 시각적 관점 (Visual Viewpoint)

= 대수적 관점과 달리, 행렬 $W$의 각 행이 이미지와 동일한 shape를 가지도록 함.
-> 가중치 각각에 대한 시각화를 할 수 있음.
-> 각 class에 대한 템플릿이 생성됨.

• 대수적 관점에서와 같이, 벡터 간 내적 연산을 수행해 입력 이미지가 각 템플릿과 얼마나 잘 맞는지 계산함.
• 그러나 템플릿을 생성한다는 특징은 Linear Classifier의 실패 요인과도 연결됨.
  

관점 3: 기하학적 관점 (Geometric Viewpoint)

예시 1) 입력 이미지가 '차'인지 아닌지 구별하는 상황

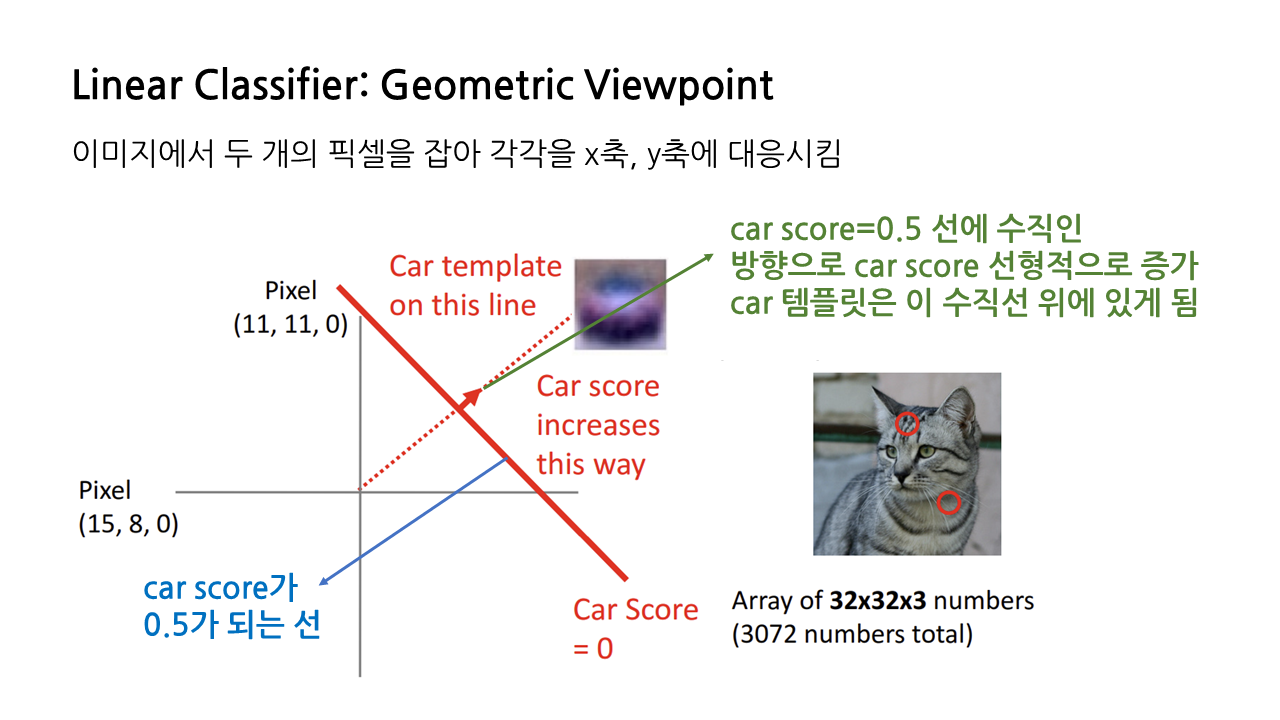
• 이미지에서 두 개의 픽셀을 잡아 각각 x, y축에 대응시킴.
• car score = 0.5인 수직선을 긋고, 이 선을 기준으로 오른쪽에 위치하면 차에 대한 점수가 높은 것으로, 왼쪽에 위치하면 차에 대한 점수가 낮은 것으로 판단함.
• 즉, car 템플릿은 car score = 0.5인 수직선의 윗부분에 있다고 볼 수 있음.

예시 2) 고차원으로의 확장

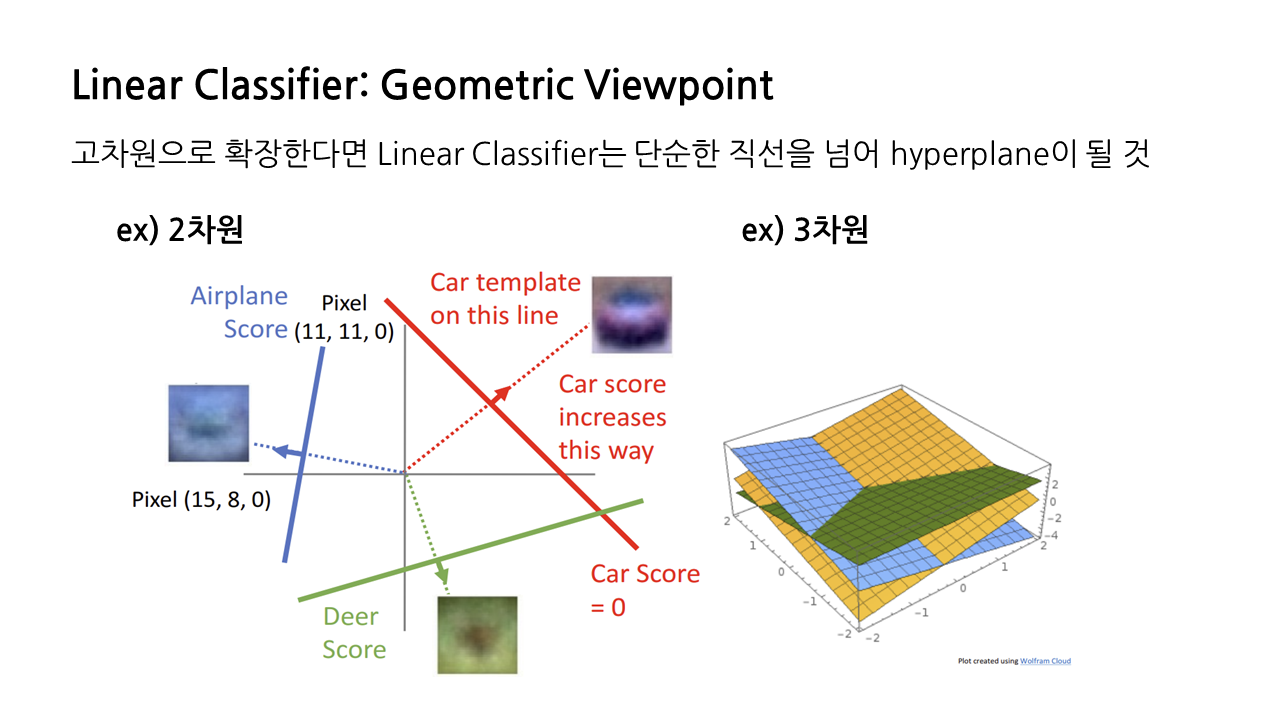
• 예시 1에서는 픽셀 두 개만을 고려한 2차원 상황이었음.
• 이를 고차원으로 확장하면 Linear Classifier는 직선을 넘어 Hyperplane으로 표현됨.

한계

1) 선형 분류가 불가능한 경우

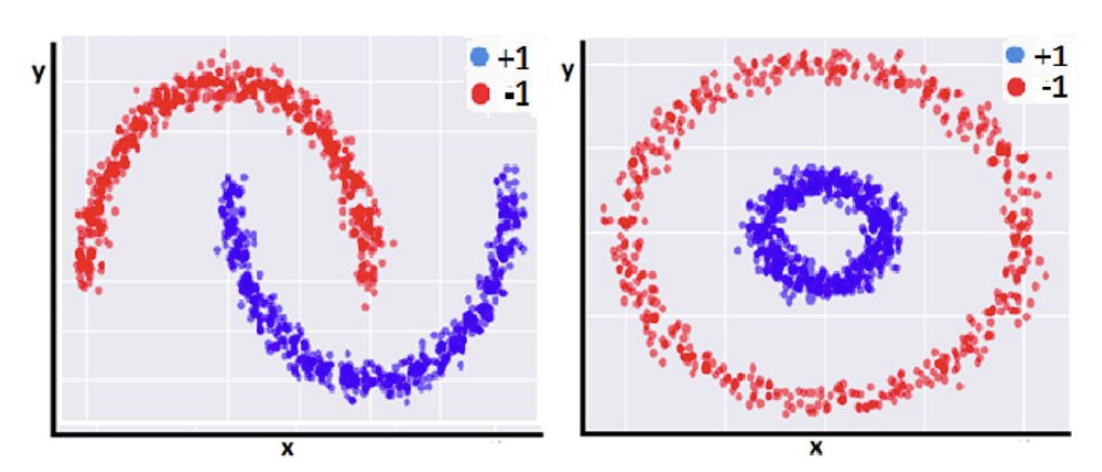
• 위 그림의 경우 하나의 선을 그어 빨간색, 파란색 영역을 구분하는 방법이 존재 X
• 즉, 복잡한 관계로 이루어진 두 개의 클래스들은 완벽히 분리할 수 없음.
  ->featurization 으로 해결

Featurization

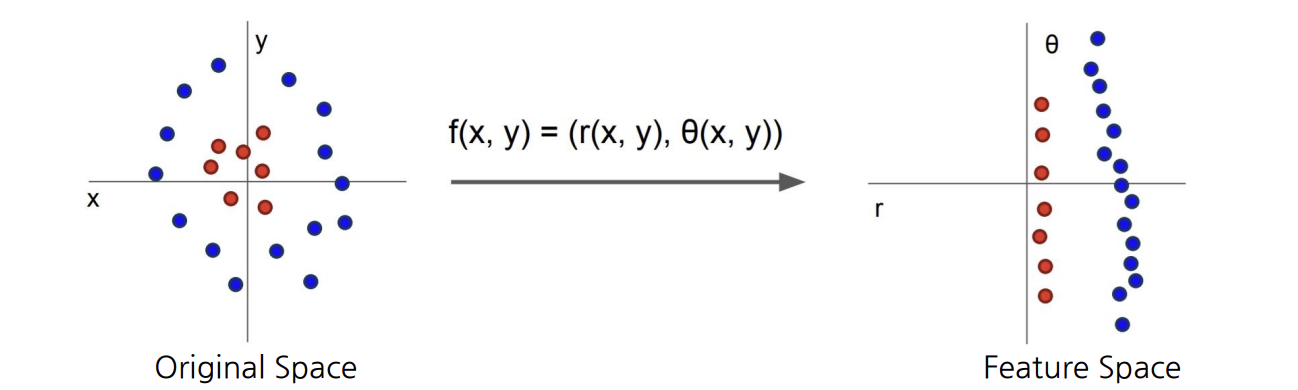
• 어떤 좌표계에서 data가 우리가 분류할 수 없는 어려운 형태로 분포되어있을 때, 해당 data point들을 다른 좌표계로 보내서 잘 분류될 수 있도록 함.
• 원본 data의 성질은 그대로 유지하되, 다른 좌표계 혹은 다른 embedding space로 옮겨 처리가 잘 되도록 함.
• 이렇게 처리된 data를 feature라고 함.

예시) 이미지 데이터를 featurization하는 고전적 기술

• pixel level의 입출력 관계를 mapping하는 대신 몇 가지 특징을 추출해 입력을 표현함.
• color histogram: 개구리 사진의 색 분포를 histogram으로 그림 -> 초록색이 많음
• HoG: 각 픽셀 당 색의 변화도를 map으로 나타냄.
• Clustered codebook: 각 patch가 어떤 패턴을 갖고 있는지로 이미지를 나타냄 e.g. 개구리의 눈, 발, 잎사귀...

-> 단점: 데이터마다 각각 다른 featurization 방법을 design, 적용해야 함 (=노가다)
-> 해결: data를 통해 featurization 방법을 배우자! (neural network)

2) '점수'의 한계

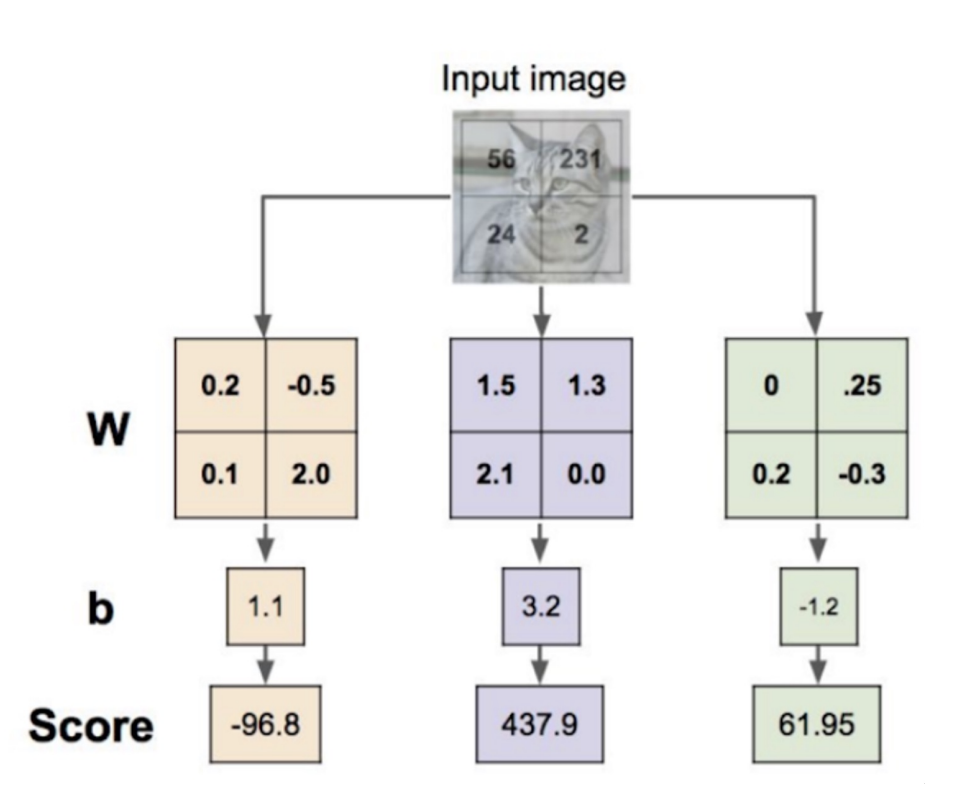
• 점수는 상한/하한의 제약이 없어 임의로 커질 수 있음.
• 또한 점수(예: 437.9)가 갖는 의미를 해석하기 어려움.
  -> 점수를 0~1로 제한해 확률로 해석하는 Softmax Classifier의 등장

---

Softmax Classifier

개념

• output인 점수를 0~1로 제한함으로써 해당 class에 속할 확률로 해석할 수 있음.
• 이진 분류에 사용되는 sigmoid 함수의 일반화된 함수인 softmax 함수를 사용 -> 다중 분류에 사용
• output 합이 1이 되도록 정규화하며, 이를 통해 각 클래스에 대한 확률 분포를 제공

Sigmoid 함수의 유도

2개의 class가 있다고 가정했을 때

• $S_1 > S_2$: 해당 이미지가 class 2보다 class 1에 속할 확률이 높음.
• $S_1 - S_2$이 클수록 $x \in C_1$일 확률이 더 높음.
• 마찬가지로 $S_2 - S_1$이 클수록 $x \in C_2$일 확률이 더 높음.

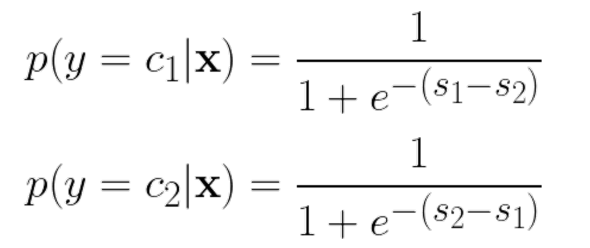
점수의 차이가 S(= $S_1 - S_2$)라고 주어질 때,

• 1에 가까울 수록 S가 커지고, 0에 가까울 수록 S가 작아지며,
• $S_1 = S_2$이면 S = 0.5이도록 하는 함수가 필요함
  -> sigmoid 함수 사용

Sigmoid 함수

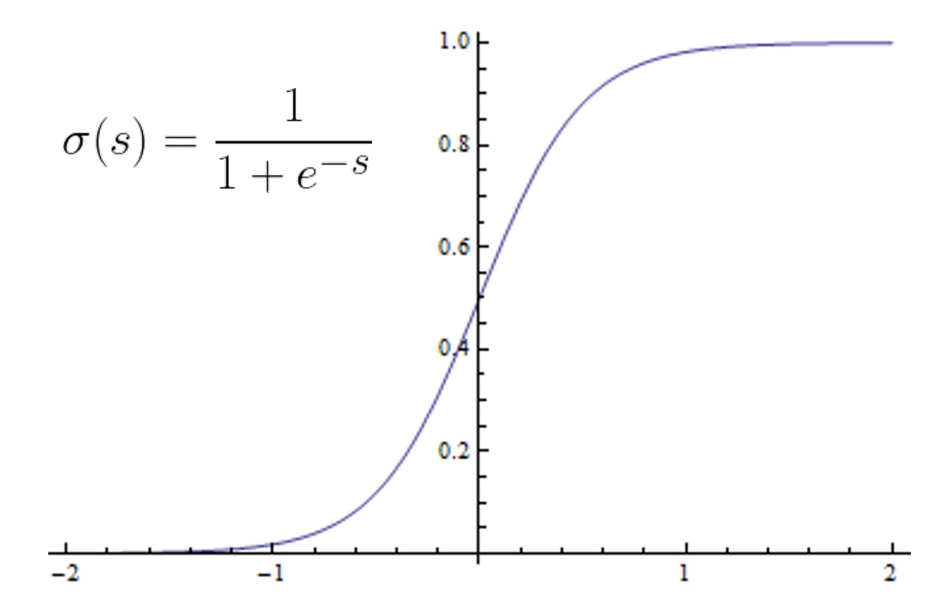
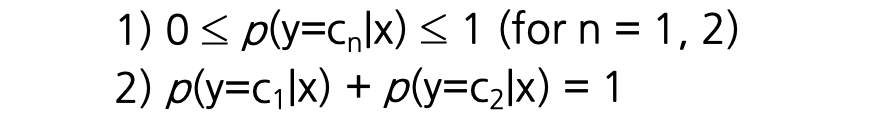
Softmax 함수

• sigmoid 함수를 class가 n>2인 경우에 대해 일반화한 함수

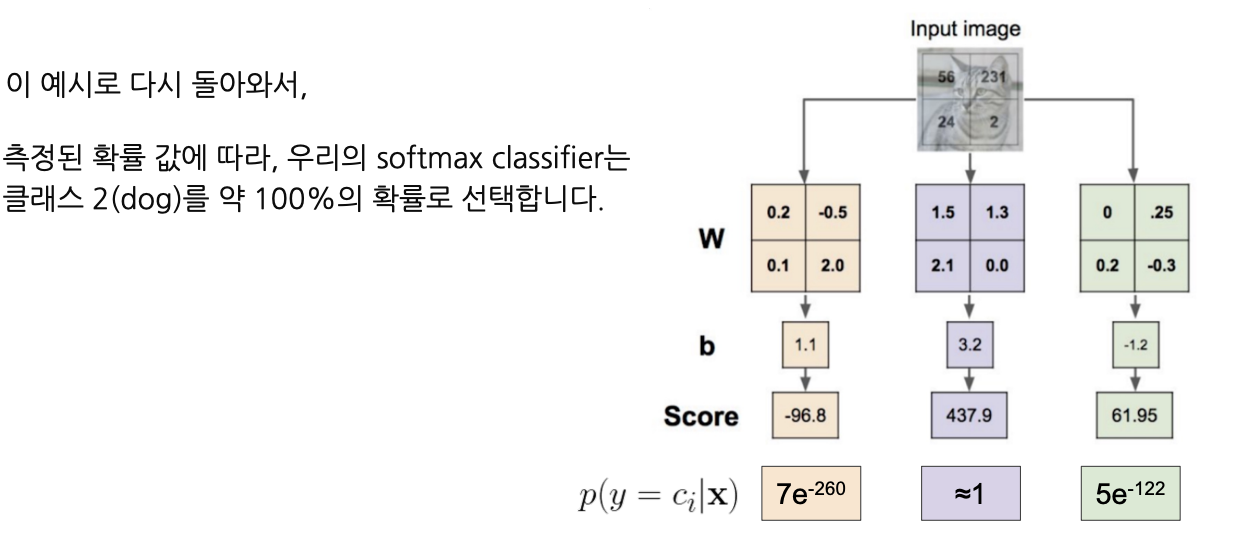
• Softmax 함수를 적용함으로써 Linear Classifier의 점수(의미가 불명확함..)를 확률(해석이 용이함!!)로 변환할 수 있음.
• Linear Classifier의 output으로 출력된 437.9에 Softmax를 적용하면 1에 가까운 값으로 변환됨.
  -> 즉, 입력 이미지가 class 2에 해당할 확률이 1(100%)에 가깝다고 해석할 수 있음.

---

Outro

더 읽어볼 것

K-Nearest Neighbors Demo
역시 명문대다

참고 자료

• https://web.eecs.umich.edu/~justincj/slides/eecs498/498_FA2019_lecture03.pdf
• https://gumgood.github.io/cs231n-2-2
• https://ydduri.tistory.com/4