[ML LifeCycle] 손실 함수(Loss Function)와 최적화(Optimization)

매개변수(가중치 $W$, 편향 $b$)의 값은 어떻게 정하면 좋을까?

1. 모델의 형식을 디자인한다. e.g. f(x, W) = Wx
2. 가중치 $W$의 값을 random하게 설정한다.
3. train data $x$를 입력하여 예측값 $\hat{y}$를 예측한다.
4. 예측값 $\hat{y}$을 실제값 $y$와 비교하여 현재 값이 얼마나 좋은지/나쁜지를 비교한다. (= 손실 함수)
5. 손실값(loss)에 따라 매개변수를 업데이트한다. (= 최적화)
   -> $\hat{y} \approx y$가 될 때까지 3~5의 과정을 반복한다.

---

손실 함수 (Loss Function)

• 해당 머신러닝 모델이 얼마나 좋은지/나쁜지 정량화하는 함수 $L(\hat{y}, y)$
• 손실함수는 다음과 같은 성질을 가져야 함.

1. $\hat{y} = y$인 경우: 모델에 페널티를 주지 말아야 하므로 손실은 (약) 0이어야 함.
2. $\hat{y} \approx y$인 경우: 작은 페널티를 주어 매개변수를 미세하게 조정해야 함.
3. $\hat{y}$와 $y$의 격차가 클 경우: 큰 페널티를 주어 매개변수를 크게 조정해야 함.

• 손실함수에는 Discriminative Setting과 Probabilistic Setting이 있으며, 실제로는 Probabilistic Setting이 많이 쓰임.

차별적 설정 (Discriminative Setting)

• 모델이 직접적으로 클래스 레이블이나 값을 예측하는 방식
• 즉, 입력 데이터를 받아 가장 가능성이 높은 class나 값을 출력

마진 기반 손실 (Margin-based Loss)

• Discriminative Setting에서 모델의 판별 성능을 강화하기 위해 사용되는 손실 함수의 종류
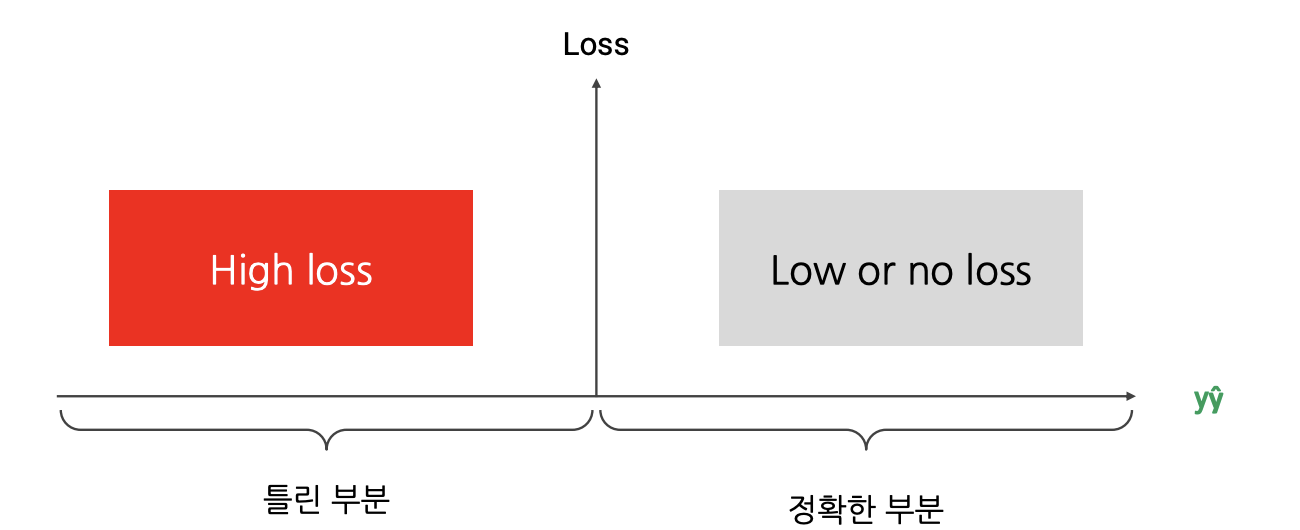
• 예측값 $\hat{y}$와 실제값 $y$의 곱 $y \hat{y}$으로 손실이 계산됨.
• 부호가 같으면 (= 분류가 정확하면) 손실이 작아지거나 0이 됨.
• 부호가 다르면 (= 분류가 틀렸으면) 손실이 커짐.
• 손실($y \hat{y}$)의 절댓값이 클수록 자신있는 예측, 작을수록 자신없는 예측임.
  

0/1 손실 (Zero-One Loss)

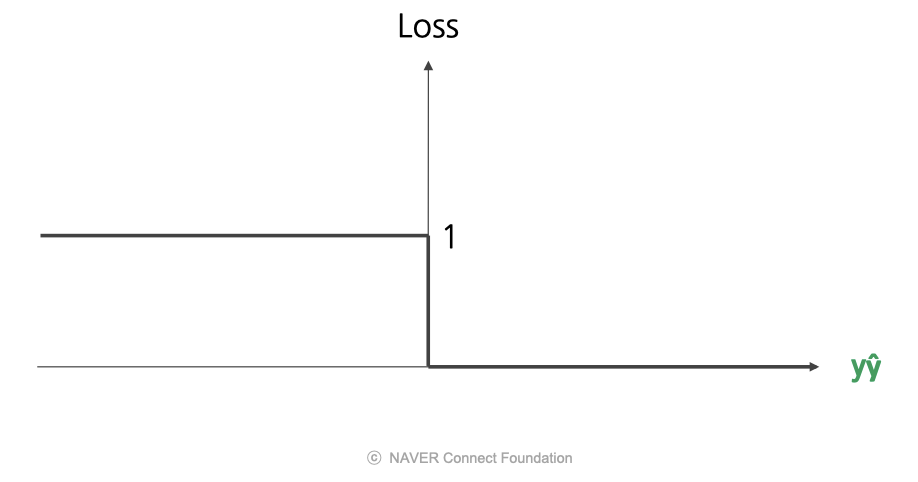
• $y \hat{y}$이 양수일 경우, 맞는 예측이므로 손실은 0을 줌.
• $y \hat{y}$이 음수일 경우, 틀린 예측이므로 손실은 1을 줌.
• 장점) 단순함
• 단점) $y \hat{y} = 0$인 지점에서 미분 불가

로그 손실 (Log Loss)

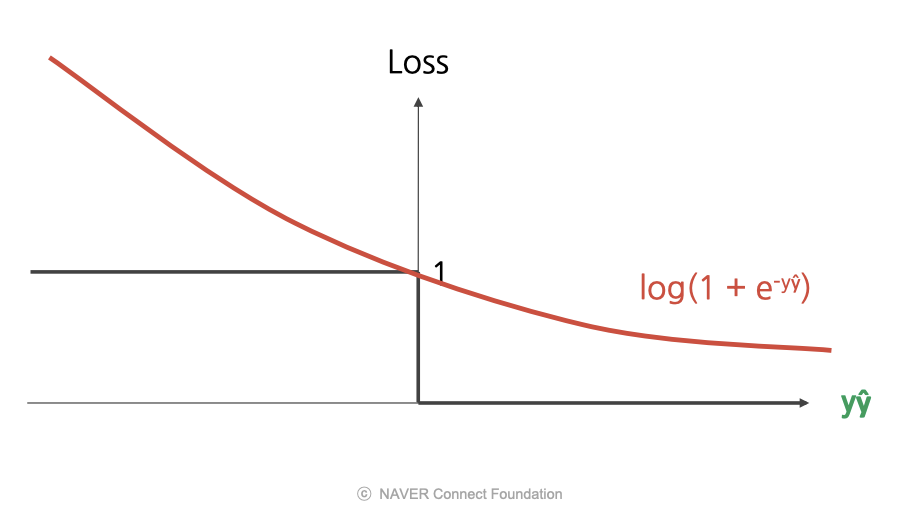
• $y \hat{y}$이 양수일 경우, 맞는 예측이므로 손실을 적게 줌.
• $y \hat{y}$이 음수일 경우, 틀린 예측이므로 손실을 크게 줌.
• 즉, 예측이 정확할수록 페널티가 작아짐.
• 장점) 연속 함수이므로 모든 지점에서 미분 가능
• 장점) 출력을 P(y|x)로 볼 수 있어 해석이 쉬움.

지수 손실 (Exp Loss)

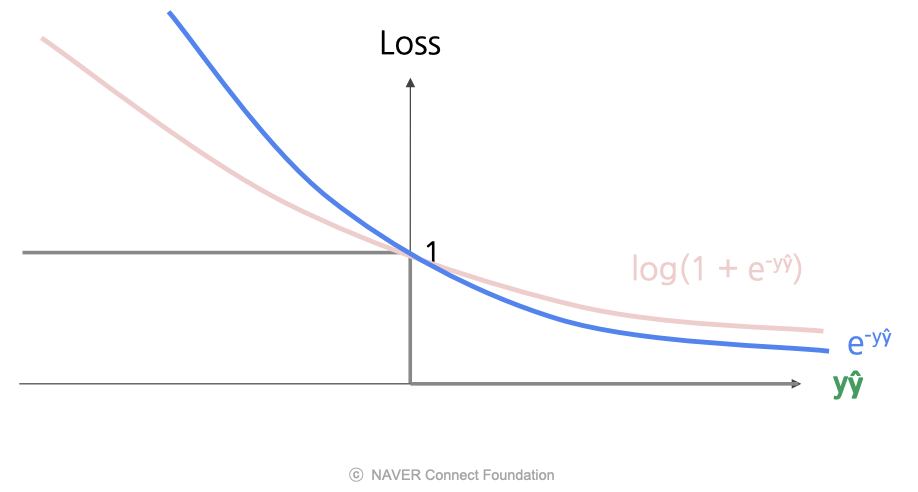
• 로그 손실과 유사하지만 더 극단적인 형태로, 로그 손실의 곡선보다 가파름.
• 잘못된 경우에는 더 엄격하게 페널티를 주고, 올바른 경우에는 적은 페널티를 줌.
• 장점) 로그 손실과 마찬가지로 모든 지점에서 미분 가능
• 단점) Outlier에 매우 큰 손실을 할당하므로 Outlier의 영향을 강하게 받음. (-> 노이즈가 많은 data에 적합 X)

Hinge 손실 (Hinge Loss)

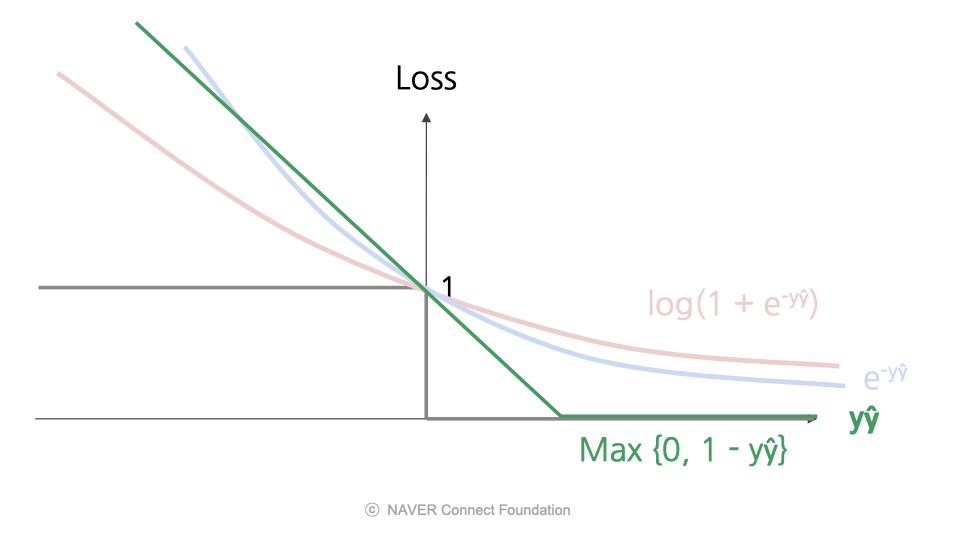
• 어느정도 자신있는 예측 + 맞는 예측 -> 손실을 주지 않음.
• 자신없게 예측 or 틀린 예측 -> 손실을 줌.
• 즉, 오류에 대한 페널티가 선형적으로 증가하며, 오차 범위 내에서 정답인 경우에도 약간의 페널티를 받음.
• 장점) 계산적으로 효율적임. (미분값이 0 혹은 1이라 미분을 하지 않아도 되므로)

마진 기반 손실의 비교

• 로그 손실, Hinge 손실이 널리 사용됨.
• 로그 손실은 출력을 P(y|x)로 볼 수 있어 해석이 쉬움.
• Hinge 손실이 계산적으로 더 효율적임.

확률적 설정 (Probabilistic Setting)

• 모델이 각 class에 속할 확률 분포를 예측하는 방식
• 즉, 입력 데이터가 주어졌을 때 각 클래스에 속할 확률을 계산

Cross Entropy, Kullback-Leibler (KL) 발산

https://hyunw.kim/blog/2017/10/26/Cross_Entropy.html
위 글 참고

---

최적화 (Optimization)

• 최적의 가중치 $W$ 및 편향 $b$를 찾는 과정
• 손실 함수 $L(\hat{y}, y)$의 값을 최소화하는 파라미터를 구하는 과정
• 예측값 $\hat{y}$과 실제값 $y$의 차이를 최소화하는 네트워크 구조와 파라미터를 찾는 과정
  
  

경사 하강법 (Gradient Descent)

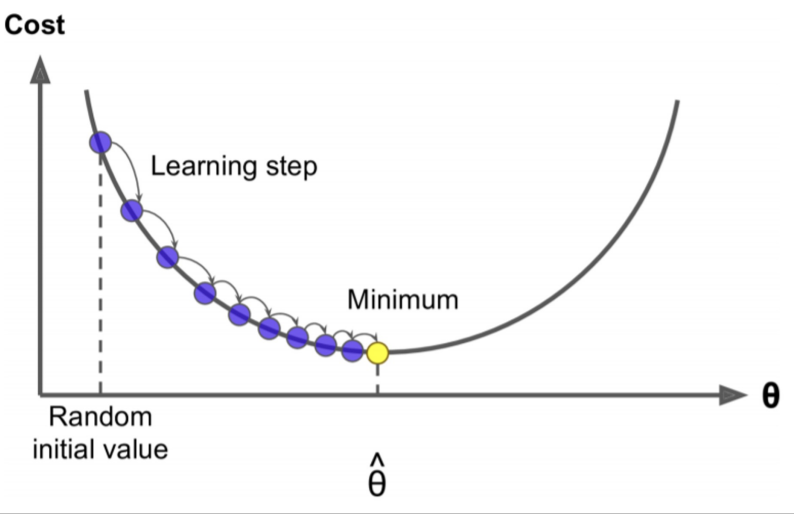
개념

• 가중치 혹은 편향에 대해, 임의의 초기값 $\theta$를 설정
• $\theta$의 현재값에 대해 손실함수 $J($\theta$)$의 기울기를 계산
• 기울기 값과 learnig rate의 곱만큼 $\theta$를 업데이트

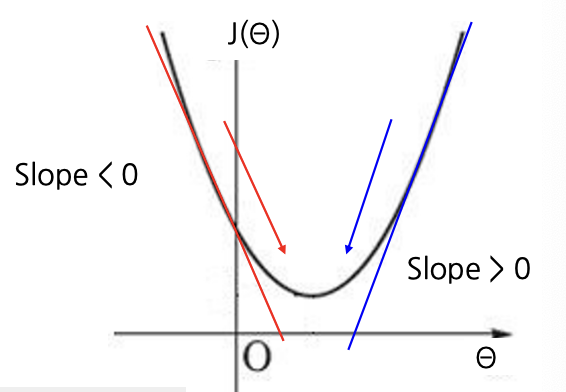
한계

1. Local Minimum에 빠지기 쉬움.
2. Saddle Point(안장점)을 벗어나지 못함.
3. 손실 함수가 미분 불가능하면 사용할 수 없음.
4. Global Minimum으로 수렴하는 속도가 상당히 느릴 수 있음.

확률적 경사 하강법 (Stochastic Gradient Descent)

개념

• 모든 train data에 대해 기울기를 계산하는 대신, 무작위로 sampling된 하위 집합 (= mini batch)에 대해서만 수행
• 일반적으로 32, 64, 128, 256, ..., 8192 크기의 mini batch로 수행
  -> 최적의 크기는 문제, 데이터, 하드웨어에 따라 다름)
• batch size가 클수록 안정적으로 업데이트, but 오래 걸림

---

Outro

더 읽어볼 것

• https://hyunw.kim/blog/2017/10/26/Cross_Entropy.html

참고 자료

• Margin-based Loss
  
• 최적화 개념과 경사 하강법