문제

풀이과정

오랜만에 다시 시작하는 알고리즘 문제, 문제에 대한 이해 보다도 이향계수자체에 대해 몰라서, 수학적 이론 부터 찾아봤던 문제였습니다. 먼저 해당 문제를 풀기 위해서는 이항 계수와, 파스칼의 삼각형에 대한 이론이 필요합니다.

이항정리

이항 정리는 두개의 항이라는 뜻 이며, 항을 옮긴다는 뜻이다.
먼저 제곱 공식에 대해 이야기 해보자.

해당 식이 저렇게 나오는 데에는 이러한 과정을 거친다. 먼저 해당 식은 이러한 형태로 바꾸는 것이 가능하다.

그 다음 해당 식에서 나타날 수 있는 총 경우의 수에 대해 이야기 해보자.
총 3가지의 경우의 수가 나타난다.

• $a$ 끼리 곱해진 경우
• $ab$ 끼리 곱해진 경우
• $ba$ 끼리 곱해진 경우
• $b$ 끼리 곱해진 경우

또한 해당 식을 $a$ 기준으로 콤비네이션 화 하면 이렇게도 표현할 수 있다.

• $a$ 끼리 곱해진 경우 => $_2C_2$
• $ab$ 끼리 곱해진 경우 => $_2C_1$
• $ba$ 끼리 곱해진 경우 => $_2C_1$
• $b$ 끼리 곱해진 경우 => $_2C_0$

$a$, $b$ 두가지 수 가운데, $a$ 로만 2번 뽑는 경우, $a$ 와 $b$ 하나씩 뽑는 경우, $b$ 로만 뽑는 경우를 모두 더한 것이 바로 제곱 공식이 되는 것이다.

이 방식대로 $(a+b)^n$ 에 대한 점화식을 세워보면 이러한 식이 만들어진다.

파스칼의 삼각형

한편 파스칼의 삼각형을 통해 이항정리의 성질을 나타내는 것이 가능하다. 다음의 그림을 보도록 하자.

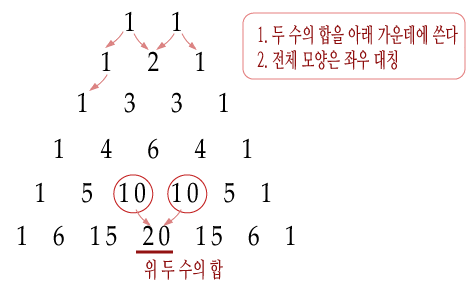
규칙은 간단하다. 맨 윗줄에 두개의 1을 써두고 아래로 내려가면서 두 수의 합을 게속 적어간다. 이를 이항 정리와 비교해보면..

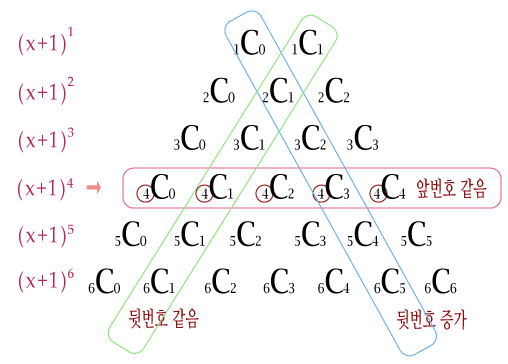
위의 그림을 토대로 규칙이 보이는가, 아래의 수들은 위의 수를 더한 값이 위의 두 수 의 가운데 부분에 나타난다. 이것이 바로 파스칼의 삼각형의 이항정리의 성질이다. 참고로 $_nC_r$ 로 파스칼의 삼각형 형태를 나타내보자면 이런식으로 나타낼 수 있다.

오답

최대 수가 1000 이었기에 단순 조합으로도 풀이가 가능하다고 생각했다. 어디서 찾아보니 이러한 식은 팩토리얼 식 구성이 나타나며 당연히 시간초과가 나올 수 밖에 없다고 한다.

import java.util.Scanner;

public class Main {
	static int N;
	static int K;
	static int[] arr;
	static boolean[] visited;
	static int ans;
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		N = sc.nextInt();
		K = sc.nextInt();
		
		arr = new int[N+1];
		for(int i=0; i<arr.length; i++) {
			arr[i] = i;
		}
		
		visited = new boolean[N+1];
		ans = 0;
		comb(1, 0);
		System.out.println(ans);
	}
	private static void comb(int num, int cnt) {
		// TODO Auto-generated method stub
		if(cnt>=K) {
			ans = ++ans % 10007;
			return;
		}
		
		for(int i=num; i<arr.length; i++) {
			visited[i] = true;
			comb(i+1, cnt++);
			visited[i]= false;
		}
	}
}

아직도 조합, 순열, 팩토리얼이 각각 어떻게 이루어지는 지 잘 이해가 가지 않는다.

정답

위의 이론들을 기반으로 DP 를 통해 계산을 하니 정답으로 인정이 되었다.

import java.util.Scanner;

public class Main {
	static int N;
	static int K;
	static int[] arr;
	static boolean[] visited;
	static int ans;
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		N = sc.nextInt();
		K = sc.nextInt();
		
		arr = new int[N+1];
		for(int i=0; i<arr.length; i++) {
			arr[i] = i;
		}
		
		visited = new boolean[N+1];
		ans = 0;
		comb(1, 0);
		System.out.println(ans);
	}
	private static void comb(int num, int cnt) {
		// TODO Auto-generated method stub
		if(cnt>=K) {
			ans = ++ans % 10007;
			return;
		}
		
		for(int i=num; i<arr.length; i++) {
			visited[i] = true;
			comb(i+1, cnt++);
			visited[i]= false;
		}
	}
}