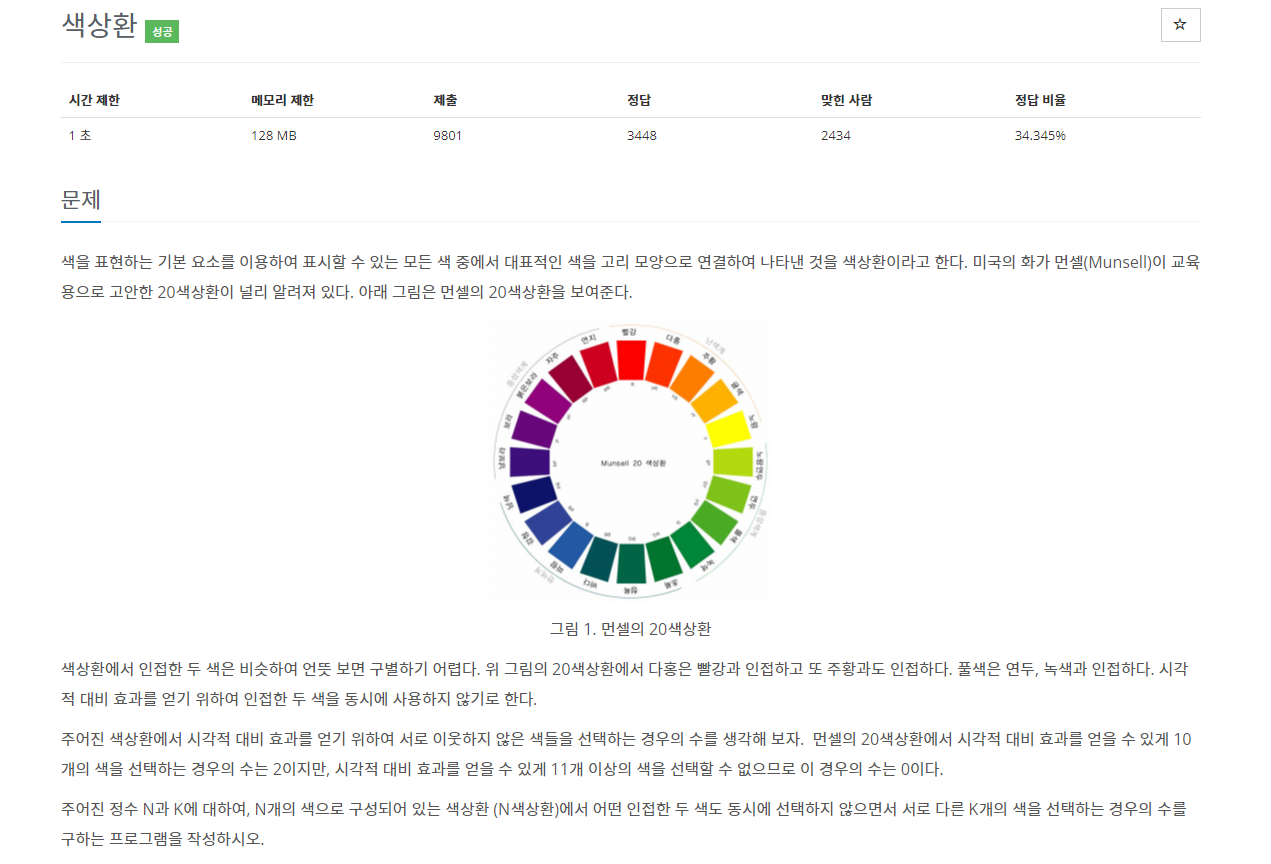
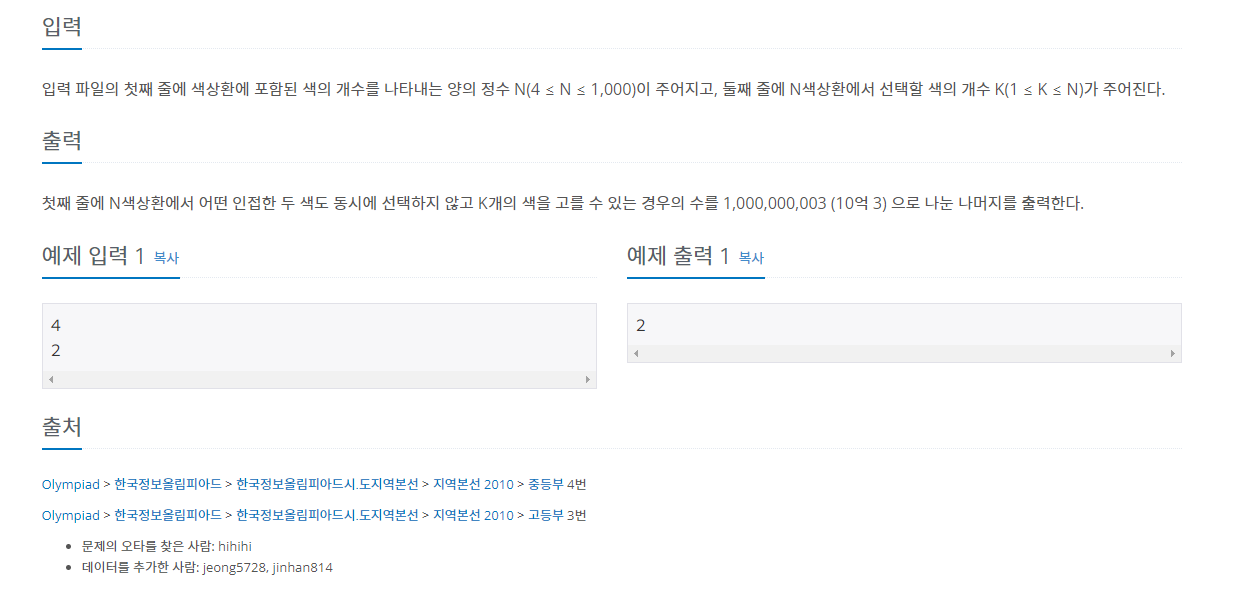
문제

풀이과정

전형적인 DP 문제. 자신에 인접한 색을 제외한 $K$ 개수 만큼의 경우의 수를 $N$ 에서 찾아야한다. 처음엔 인접하다길래 그래프인가 싶었지만, $_nC_k$ 의 모든 경우를 탐색해야하므로, 완탐시 시간초과가 날 수 있다고 예상. 분명 누적하여 진행하는 공식이 있을거라고 추측했다.

수학이랑 친하지 않은 편이라, 늘 DP 문제에서는 점화식을 세우기보다는 일일히 작성해보며 규칙을 찾곤 한다.

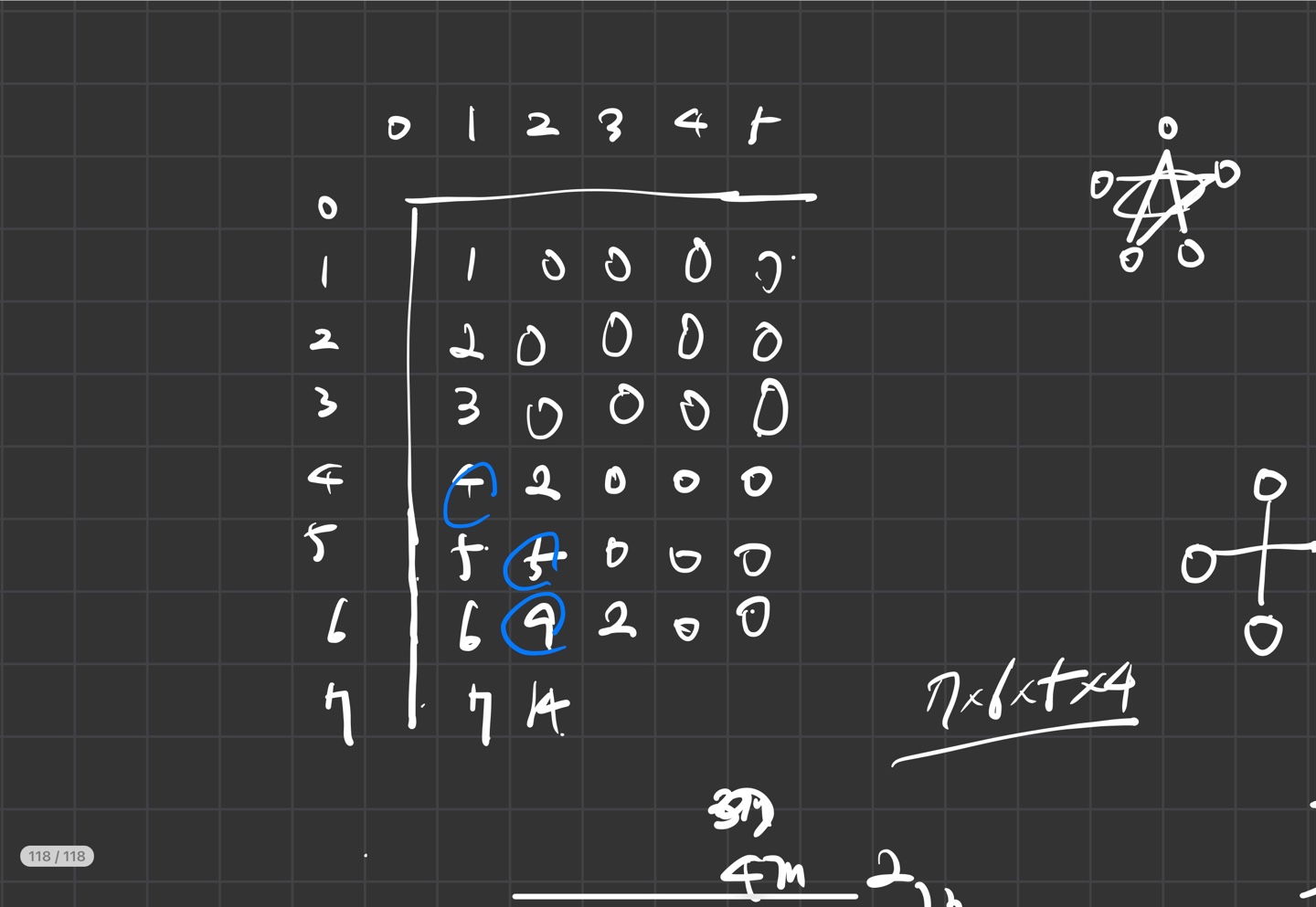
규칙 1

$N$은 색의 총 갯수, $K$ 는 뽑아야 하는 가짓수라고 한다면, 일단 $K=1$ 인 경우에는 자신만 뽑히니 $N$ 가지의 경우의 수가 나온다.

규칙 2

$N/2$ 보다 $K$는 클 수 없다. $N=2$ 인데 3가지 경우의 수를 뽑을 순 없지 않은가? 또한 인접한 수는 제외되기 때문에, 자신과 인접한 2가지 수를 제외하면 $N$ 은 적어도 4 이상이어야 한다.

점화식

이를 기반으로, 직접 그려가며 확인해본 결과 다음과 같은 규칙을 발견할 수 있었다.

오답

출력 값은 반드시 1e9+3 을 나눈 나머지 값으로 나오게 하라고 하였다. 1e9+3 으로 나머지 값을 찾으니 double 값을 나타내게 되어서, 이를 int 화 시켰더니 다른 답이 나오게 되었다.

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int N = sc.nextInt();
        int K = sc.nextInt();

        int[][] dp = new int[N+1][K+1];

        for(int i=1; i<dp.length; i++) dp[i][1] = i;

        for(int i=4; i<=N; i++) {
            for(int j=2; j<=K; j++) {
                dp[i][j] = (dp[i-2][j-1] + dp[i-1][j]) % (int) 1e9+3;
            }
        }
        System.out.println(dp[N][K]);
    }
}

$N=4$, $K=2$ 를 가지고 디버깅을 진행해본 결과 $N=4$, $K=2$는 2 가 나와야 하는데, 5 의 값이 나왔다.

정답

1e9+3 을 전체적으로 int화 시키니 답이 제대로 나왔다. 어떤 부분이 다른 건지는 잘 모르겠다. 점화식을 세우는 것도 그렇지만, 이러한 부분에서 시간을 많이 뺏기는 것이 아쉬웠다.

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int N = sc.nextInt();
        int K = sc.nextInt();

        int[][] dp = new int[N+1][K+1];

        for(int i=1; i<dp.length; i++) dp[i][1] = i;

        for(int i=4; i<=N; i++) {
            for(int j=2; j<=K; j++) {
                dp[i][j] = (dp[i-2][j-1] + dp[i-1][j]) % (int) (1e9+3);
            }
        }
        System.out.println(dp[N][K]);
    }
}

언제쯤 수학이랑 친해지려나...