기본적인 PCA 공부를 다시 해봣다... 앞서 정리하고 있던 이상탐지 리뷰 논문에서 이상탐지 방법론 중에 하나로 PCA를 통한 차원축소 후, 이 차원 축소 PC 값을 이상탐지에 사용하는 걸 얘기하고 있었다. 오랜만에 기억도 되살릴 겸 정리해보고 있다.

PCA(Principal Component Analysis)

애정하는 rastgo's blog 에 잘 정리되어 있어서, 따로 정리하지 않고 쏵 오랜만에 읽어 보았다.

중요한 점을 정리하자면,

✅ 선형변환한 데이터의 분산이 클 수 있게(즉 데이터가 PC 축에 최대한 퍼지도록) PC 축을 잡아야 한다.
✅ PCA 수행 방법 :

• 1) 기존 데이터 X 의 공분산행렬 계산
• 2) 공분산행렬의 고유값과 고유벡터 계산
• 3)고유값의 크기 순서대로 고유벡터를 나열
• 4) 정렬된 고유벡터 가운데 일부 선택
• 5) 해당 고유벡터와 X내적

✅PCA의 목적은 원데이터 행렬 X의 분산을 최대한 보존하는 데 있기 때문에 Z의 분산 또한 최대화되어야 합니다.

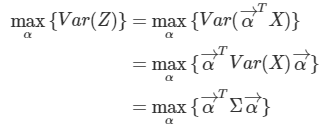
✅ 공분산행렬 Σ의 서로 다른 고유벡터끼리는 서로 직교(orthogonal)함을 확인할 수 있습니다.
✅ 원데이터를 공분산 행렬의 고유벡터로 사영하기 전에는 변수 간 연관성이 있었더라도 PCA 변환에 의하여 좌표축이 바뀐 데이터들은 서로 무상관(uncorrelated)이게 됩니다.

Kernel Principal Component Analysis

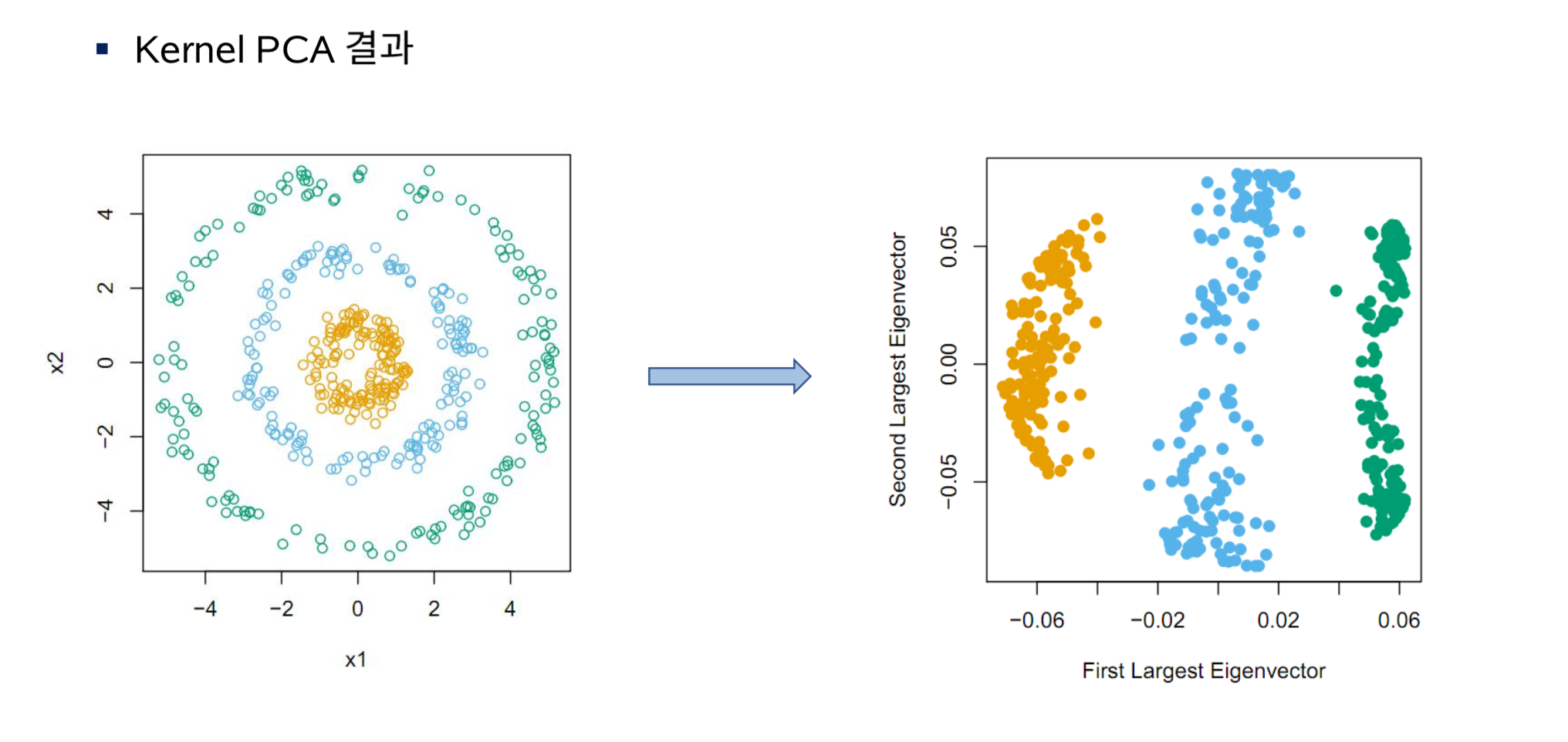
• Kernel PCA의 기본 아이디어: 표준 내적 대신 비선형 커널 함수 𝑘를 사용함으로써, 고차원 공간 𝐹에서 PCA를 암묵적으로 수행합니다. 이 고차원 공간 𝐹는 입력 공간과 비선형적으로 관련되어 있습니다.
• 커널 함수의 역할: 비선형 관계를 고려하여 데이터의 구조를 더 잘 반영할 수 있도록 합니다.

1) Linear PCA: 입력 공간에서 표준 내적을 사용하여 주성분을 찾습니다.
2) Kernel PCA: 비선형 커널 함수를 사용하여 입력 공간을 고차원 피처 공간으로 매핑하고, 그 공간에서 PCA를 수행합니다.

간단 수식

우선 데이터를 기존 D차원에서 더 고차원인 M차원으로 변환한 ɸ(x)를 상정합니다. ɸ(x)에 PCA를 적용하면 아래와 같이 식이 전개됩니다.

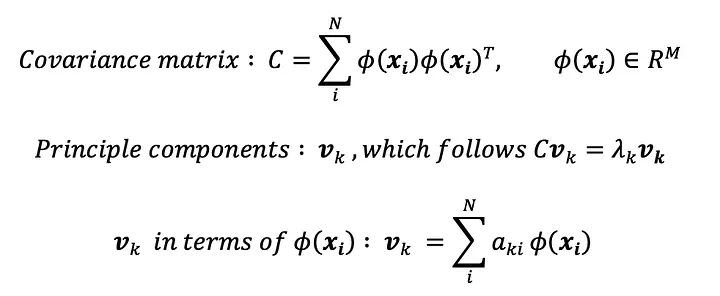
마지막 식을 ɸ(x)에 대해 풀면 연산이 굉장히 복잡해지지만, 커널트릭은 이를 ‘커널 함수’라고 불리는 k(x, x) 로 대체해 매우 간단한 연산으로 치환시킵니다. 중간 유도과정은 생략하고 우리가 찾고자 하는 주성분 v를 구하는 식으로 정리하면 아래와 같습니다.

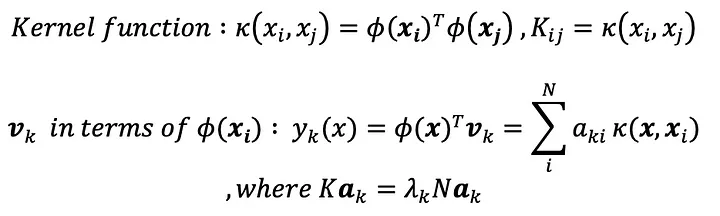
즉, 커널함수를 통해 ɸ(x)를 명시적으로 구하지 않고서도 데이터를 고차원으로 옮긴 후 PCA를 적용한 값을 구할 수 있다는 게 커널PCA의 핵심입니다.

커널함수로는 대표적으로 2가지를 사용합니다. 다항커널함수(Polynomial kernel function)과 가우시안 또는 RBF커널함수입니다.

❗ 실제로 피처 공간 𝐹로 명시적으로 매핑하는 것은 불가능하며, Kernel PCA는 고차원 문제를 해결하기 위해 커널 함수 𝑘를 사용 => Kernel PCA는 매우 높은 차원의 공간에서 내적을 계산하는 대신, 커널 함수 평가를 통해 효율적으로 주성분 분석을 수행합니다.

Kernal PCA 코드

# Kernel PCA with Polynomial kernel
def poly_kpca(X, degree, n_components, coef0=1):
 K = (np.dot(X, X.T) + coef0) ** degree
 N = K.shape[0]
 one_n = np.ones((N, N)) / N
 K = K - one_n.dot(K) - K.dot(one_n) + one_n.dot(K).dot(one_n)
 eigvals, eigvecs = eigh(K)
 pc = np.column_stack((eigvecs[:, -i] for i in range(1, n_components + 1)))
 return pc
pc = poly_kpca(X, 5, 2) #degree=5로 설정
x1 = pc[:,0]
x2 = pc[:,1]
plt.figure(figsize=(6,6))
plt.scatter(x1[y==100], x2[y==100], c='b', alpha=0.5, label='Class1')
plt.scatter(x1[y==30], x2[y==30], c='r', alpha=0.5, label='Class2')
plt.legend()
plt.show()

🔖 Reference
참고1
참고2