부캠 시작 4일차, AI를 위한 통계, 수학 강의들을 들었다. 원래 전공이 응용통계학이기에 전에 것들을 복습하는 관점에서 영상을 보았다.

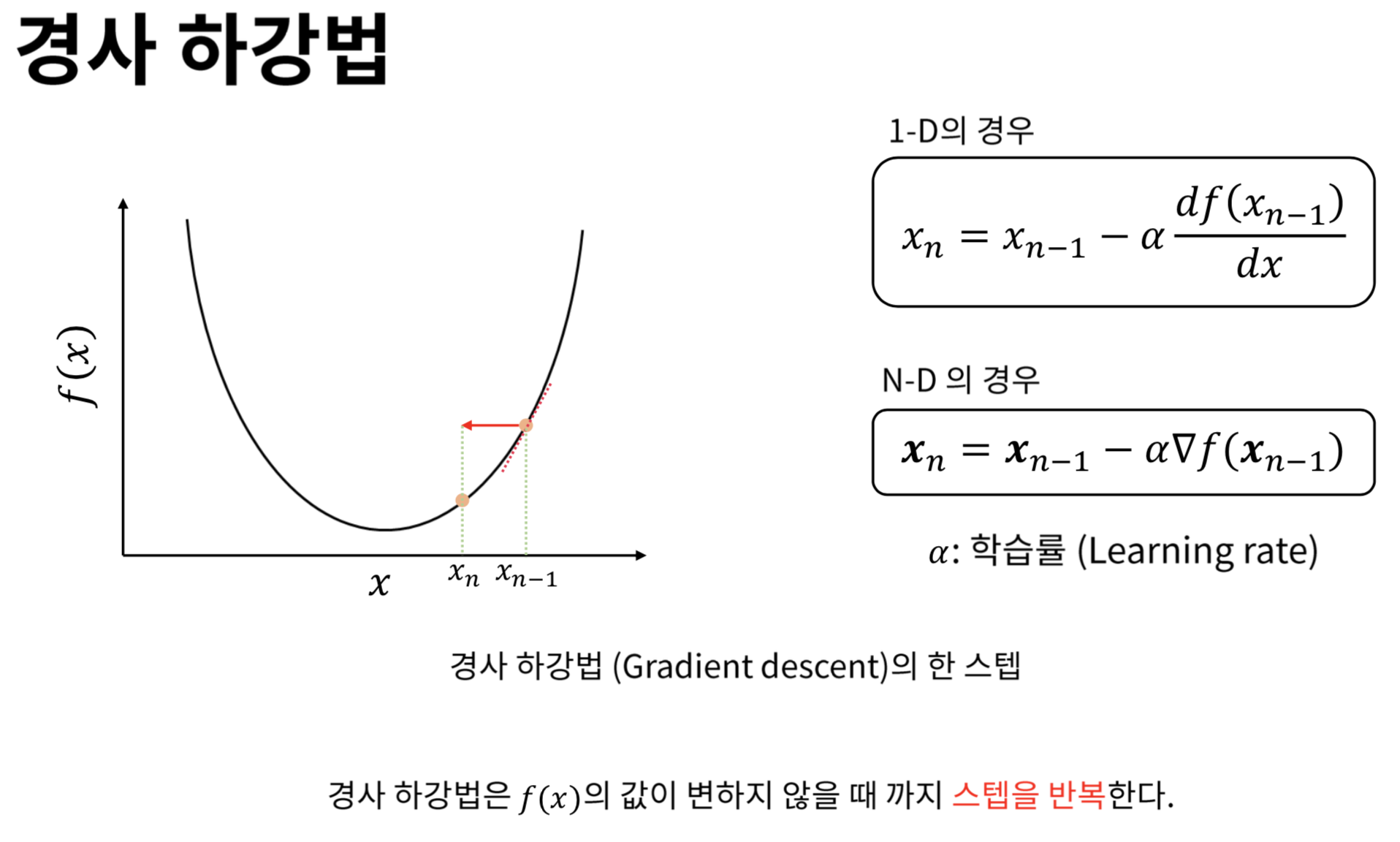
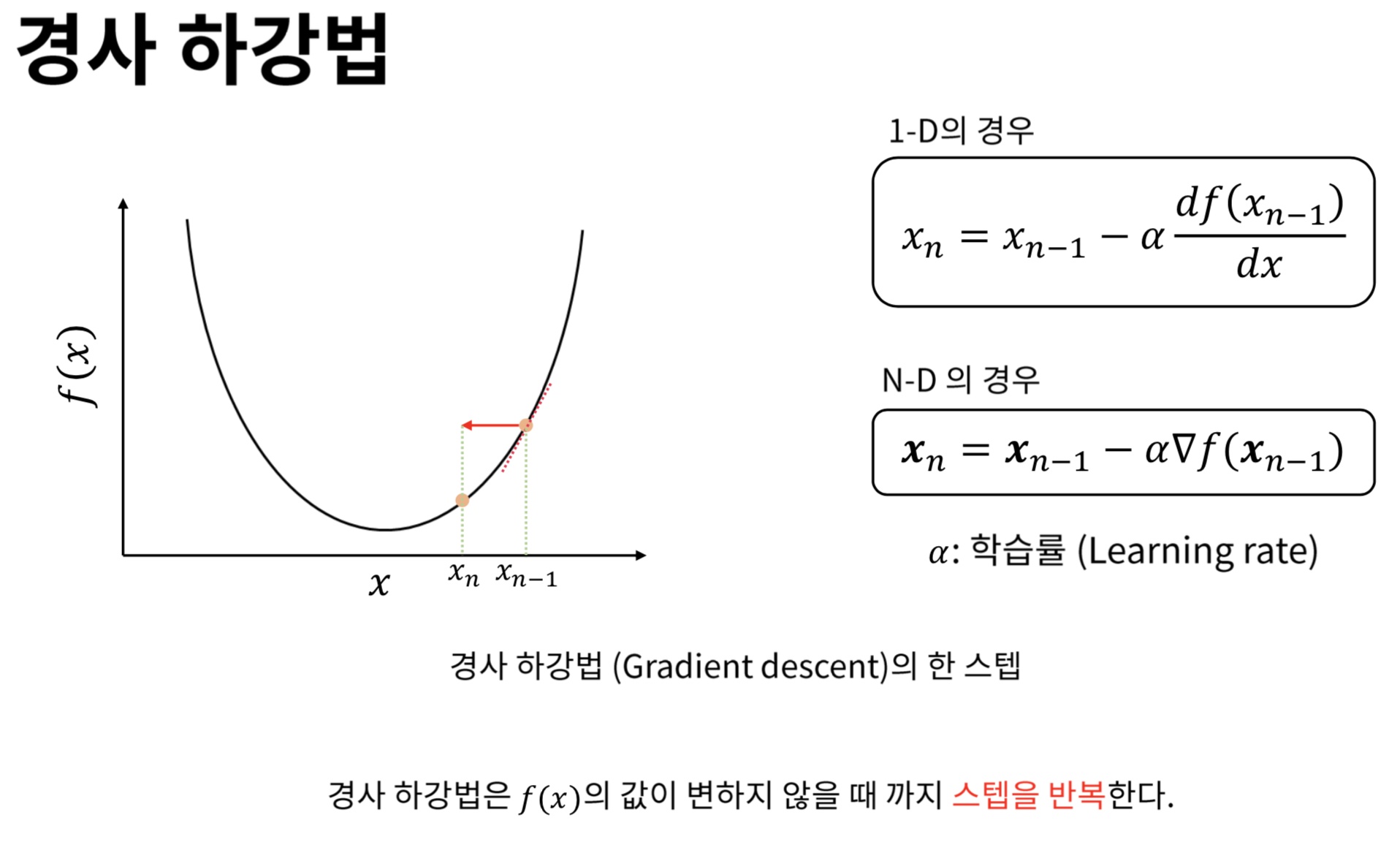
경사하강법, 딥러닝 학습 방법에 대해서 배웠는데 기억에 남기고 싶거나 중요한 내용들을 다시 한 번 정리해보려고 한다.

📖공부내용 간단 정리

경사상승법, 경사하강법의 차이

경사상승법, 목적함수의 극대값 찾기

경사상승법 : 기존 값(x)에 미분값(gradient)를 더해주는 것

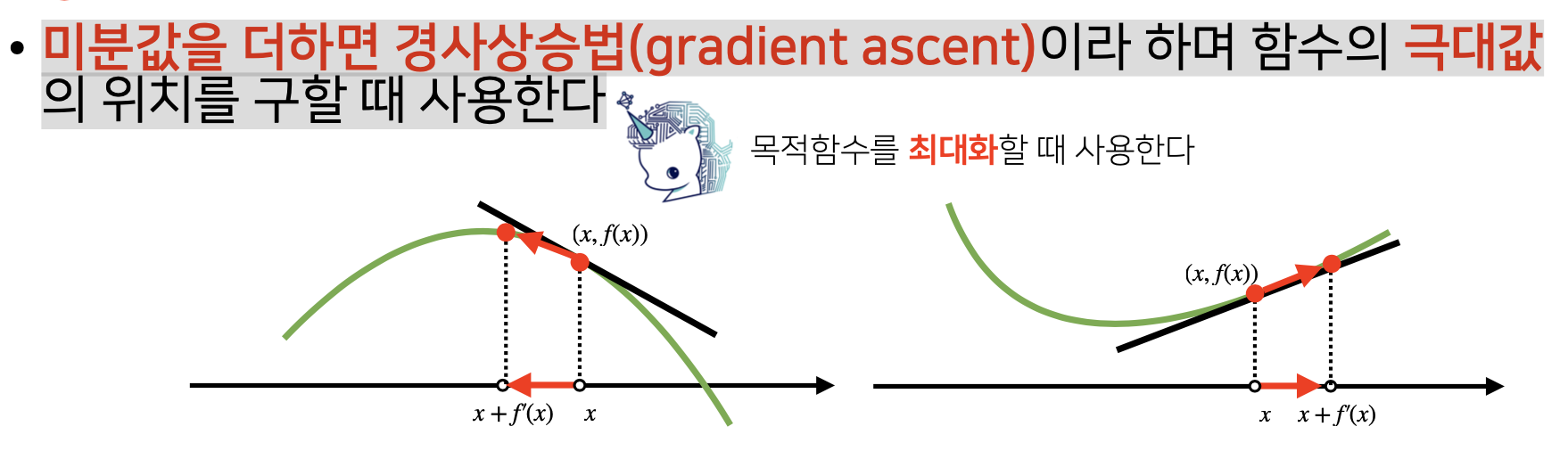
1) 미분값이 양수 (gradient 값, 즉 f'(x)가 양수)
미분값이 양수라는 것은 그림이 오른쪽처럼 증가하는 위치에 x값이 놓여있기에, 최대 값을 찾으려면 x + f'(x)를 해서 x + f'(x) > x 가 되어 x 값이 우측으로 이동하고 목적함수의 값이 극대값을 향해 가게 된다. (=>함수값이 증가함)

2) 미분값이 음수 (gradient 값, 즉 f'(x)가 음수)
미분값이 음수라는 것은 그림이 왼쪽처럼 감소하는 위치에 x값이 놓여있기에, 최대 값을 찾으려면 x + f'(x)를 해서 x + f'(x) < x 가 되어 x 값이 좌측으로 이동하고 목적함수의 값이 극대값을 향해 가게 된다. (=>함수값이 증가함)

결론적으로 경사상승법은 미분값을 기존값(x)에 더해주면서, 미분값의 부호와 상관없이 함수값이 증가하여 극대값을 향해 가도록 함.

경사하강법, 목적함수의 극소값 찾기

경사하강법 : 기존 값(x)에 미분값(gradient)를 빼주는 것

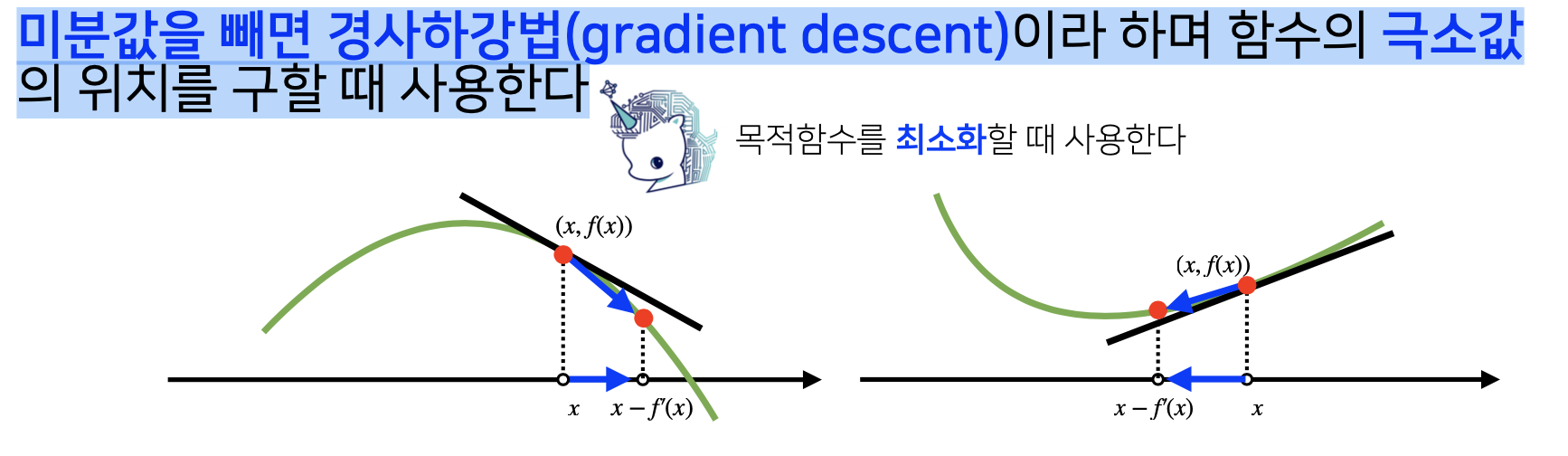
1) 미분값이 양수 (gradient 값, 즉 f'(x)가 양수)
미분값이 양수라는 것은 그림이 오른쪽처럼 증가하는 위치에 x값이 놓여있기에, 최솟값을 찾으려면 x - f'(x)를 해서 x - f'(x) < x 가 되어 x 값이 좌측으로 이동하고 목적함수의 값이 극소값을 향해 가게 된다. (=>함수값이 감소함)

2) 미분값이 음수 (gradient 값, 즉 f'(x)가 음수)
미분값이 음수라는 것은 그림이 왼쪽처럼 감소하는 위치에 x값이 놓여있기에, 최댓값을 찾으려면 x - f'(x)를 해서 x - f'(x) > x 가 되어 x 값이 우측으로 이동하고 목적함수의 값이 극소값을 향해 가게 된다. (=>함수값이 감소함)

결론적으로 경사하강법은 미분값을 기존값(x)에 빼주면서, 미분값의 부호와 상관없이 함수값이 감소하여 극소값을 향해 가도록 함.

np.linalg.pinv을 이용한 선형회귀식