Transformer

LSTM이나 GRU 기반의 Seq2seq 모델의 추가적인 add on 모듈로서 attention을 사용했었다면, 시퀀스 데이터를 입력/출력으로 처리할 때 사용할 때 사용하는 LSTM이나 GRU 혹은 전반적인 RNN 모델 자체를 이제는 attention 모듈만을 사용하는 것으로 대체한 것이 바로 Transformer이다. 그래서 논문 제목이 "Attention is all you need"

1. Long-Term Dependency

• Long-Term Dependency 문제를 해결하기 위한 시도로 Bi-directional RNN 등이 있었다. 그러나 transformer는 long-term dependency 문제를 근본적으로 해결해주었다.

1) Bi-directional RNN

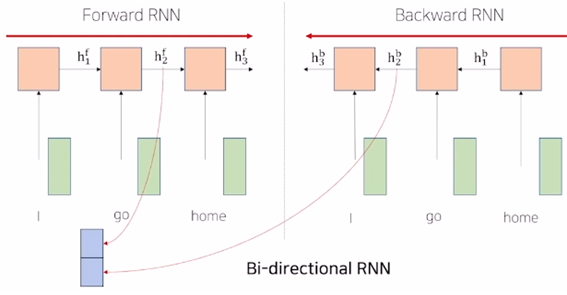
• forward RNN : I go home 이라는 문장에서 I에 대한 인코딩 벡터에 go와 home 에 대한 정보를 담을 수 없다.
• backward RNN : 정보를 오른쪽에서 왼쪽으로 인코딩한다. forward RNN과는 다른 별개의 파라미터를 가진다.
• ex) $h_2^b$에는 go 와 home에 대한 정보가 들어있다.
• forward RNN과 backward RNN 두 개의 모듈을 병렬적으로 만든다. go에 대한 단어의 hidden state vector인 $h_2^f$와 $h_2^b$ 두 개를 concat 해서 차원을 두배로 만든 벡터가 바로 go에 대한 encoding vector라고 볼 수 있다.

2) Transformer

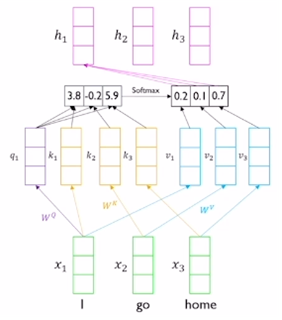
• 트랜스포머에서 제안된 attention 모듈은 RNN을 대체한다.
• Seq2seq with Attention에서 decoder의 hidden state vector에 해당하는 것이 바로 input 중에서 지금 인코딩하려는 벡터이다. (예를 들면 I)
• encoder의 각 word에 대한 hidden state vector에 해당하는 것이 I, go, home 각각에 대한 벡터이다.
• 즉 decoder 의 hidden state vector와 인코더의 hidden state vector의 구분 없이, 동일한 set의 벡터들 내에서 유사도를 계산할 수 있다는 측면에서 self-attention 모듈이라 부른다.
• 주어진 query가 어느 key와 유사도가 높은지 내적으로 구하고, 산출된 점수에 softmax를 취해 가중치를 얻는다. 이 가중치와 value 벡터의 선형결합으로 하나의 output vector를 얻는다. (유사도 계산 시 나 자신과의 유사도와 다른 벡터와의 유사도 모두 구하는 것이다.)
• 그런데 자신과의 내적은 다른 벡터와의 내적에 비해 대체로 유사도가 크게 나온다. 결국 자기 자신에 큰 가중치가 걸리는 attention vector의 양상이 나타날 것이다. 이런 부분을 개선하기 위해서 query, key, value를 만들 때 각각 다른 변환 행렬을 사용해준다.
• 모든 벡터가 다 query, key, value 벡터가 된다.

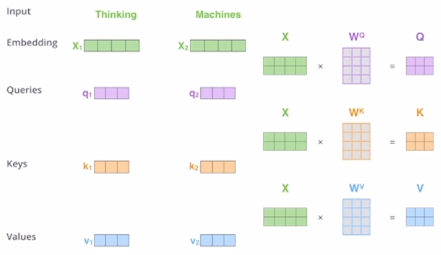
• 행렬 관점으로 보면 위와 같다. Q 행렬의 1행이 $q_1$에 해당한다.

Bi-directional RNN처럼 self-attention 모듈도 인코딩 벡터를 만들 때 모든 input 벡터를 다 적절하게 고려한다는 것을 알 수 있다. 그러나 중요한 차이점은 sequence 길이가 매우 길다 하더라도 self-attention 모듈을 적용해서 시퀀스 내의 각각의 워드들을 인코딩 벡터로 만들게 되면 어느 워드에 대해 인코딩 벡터를 만들든 항상 동일한 key 벡터와 value 벡터로 변환이 된다. 따라서 타임스텝의 gap이 굉장히 멀다 하더라도 내적에 의한 유사도만 높다면 정보를 손쉽게 가져올 수 있다. 먼 타임스텝의 정보를 가져오려면 여러 개의 RNN 모듈을 연속적으로 통과시킴으로써 정보의 손실/변형이 일어나는 문제 (Long-term dependency 문제)를 근본적으로 해결해준 것이 바로 transformer이다.

2. Scaled Dot-product Attention

Self-Attention을 수식으로 나타내면 다음과 같다.

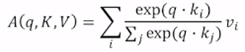
• input : a query $q$, and a set of key-value $(k, v)$ pairs to an output
• 쿼리, 키, 밸류, 아웃풋 모두 벡터이다.
• output은 value 벡터들의 가중 평균이다.
• 각 value의 weight는 query와, 그 query에 대응되는 key의 내적으로 계산된다.
• query와 key는 dimension이 같아야 한다. value의 차원은 꼭 같지 않아도 된다. vector에 대해서는 가중치만큼 상수배하여 가중평균을 얻기 때문이다.
• output vector는 value 에 대한 가중평균이므로 차원은 value 벡터와 동일하다.

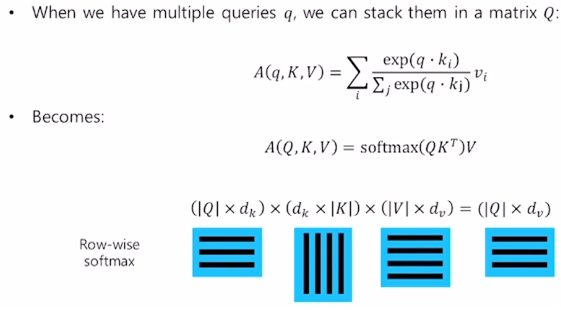
• $QK^T$에서 각 행은 각각의 query에 대한, 내적에 기반한 key들과의 유사도를 의미한다. i번째 행 j번째 열이라면 i번째 query와 j번째 key의 유사도를 의미한다.
• softmax를 행렬에 적용해줬을 경우 row-wise를 default로 생각한다. (즉 softmax 결과 각 행이 [0,2 0.1 0.4 0.3] 꼴로 나올 것이다.)
• softmax를 적용해 구한 가중치 행렬과 V(value 행렬)을 곱한 결과 각 행은 각 query에 대한 attention 모듈의 output 벡터(encoding vector)가 된다. (결과 행렬의 i행은 가중치 행렬의 i행과 V 행렬에 대한 row-wise 곱으로 생각할 수 있으므로 i번째 query에 대한 value 벡터들의 가중평균 벡터.)
• 이렇게 행렬 연산으로 바꿔서 병렬화해주면 gpu를 활용하여 매우 빠르게 연산 가능하다.

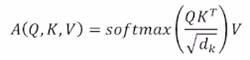
• dot-product를 수행할 때는 scaeld dot-product를 수행해야 한다. 내적에 참여하는 query와 key의 차원(dimension)에 따라 내적값의 분산이 좌지우지 될 수 있기 때문이다. 차원이 커질수록 분산이 커질 수 있다. 그리고 분산이 클수록 softmax를 통과시켜 얻은 가중치가 어느 한 key에만 몰리는 현상이 발생할 수 있다.
• 따라서 내적값의 분산을 일정하게 해줌으로써 학습을 안정화하기 위해 scaled dot-product를 수행한다. (query와 key의 dimension인 $d_k$의 제곱근 값으로 scaling을 해준 뒤 softmax를 통과시킨다.)
  $QK^T$의 각 요소를 $\sqrt{d_k}$로 나눠주는 것이다.
• softmax의 값이 한쪽으로 매우 치우치는 경우 학습 시에 gradient vanishing이 발생하여 학습이 전혀 되지 않기 때문에 scaled dot-product는 학습에도 굉장히 중요한 역할을 한다.
  
  

3. Multi-Head Attention

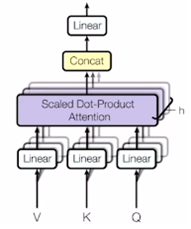
• self-attention 모듈을 좀 더 유연하게 확장.
• 동일한 Q, K, V에 대해 병렬적으로 여러 버전의 self-attention을 수행하는 것을 말한다.
• 그림의 중첩된 블록들이 Multi-Head Attention (이하 MHA)를 표현하고 있다.

1) MHA의 구조

• 여러 버전의 선형변환 행렬들이 존재한다. $i$번째 head에서는 $W_i^Q$, $W_i^K$, $W_i^V$를 사용하는 것이다.
• 동일한 쿼리 벡터에 대하여 서로 다른 버전의 어텐션의 개수만큼 서로 다른 버전의 인코딩 벡터들을 얻게 되고 이 벡터들을 모두 concatenate 함으로써 그 쿼리 벡터에 대한 최종적인 인코딩 벡터를 얻는다.
• attention을 수행하기 위한 서로 다른 선형변환 matrix들을 head라고 부르기 때문에 Multi-head Attention이라 한다.
• 각각의 head는 서로 다른 정보를 병렬적으로 뽑아내는 역할을 한다. 동일한 시퀀스에 대하여 여러 다른 측면의 정보를 가져와야 할 때 사용할 수 있다. (시간 정보, 장소 정보, 행동 정보 등)

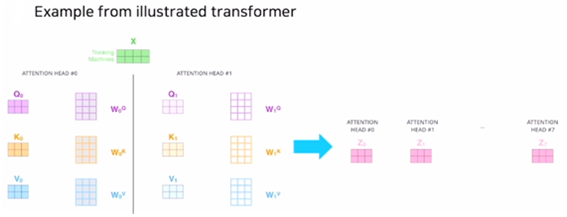
• 두 개의 쿼리
• query 벡터와 key 벡터의 차원은 3
• value 벡터의 차원 : 3
• 8개의 head 가 있는 MHA

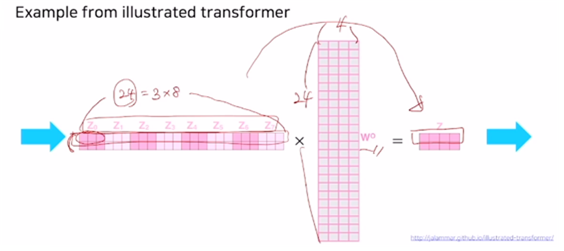
• concat 결과 하나의 쿼리에 대한 인코딩 벡터는 24(=3*8) 차원의 벡터가 된다.
• $W^O$는 최종 output인 Z로 줄여주는 또다른 선형변환 역할을 한다.

2) 계산 측면에서 요구되는 Attention 모듈의 메모리 요구량. (RNN 기반의 시퀀스 인코딩과 비교)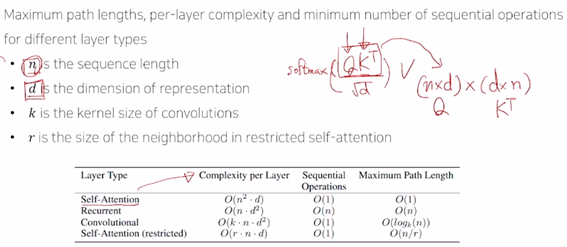

(1) 메모리 요구량

• self-attention에서 주된 계산을 차지하는 것은 $QK^T$ 부분이다. Q와 K의 차원이 위와 같다고 할 때 O($n^2$ $\cdot$ $d$)의 시간 복잡도를 가진다. 그러나 이러한 행렬 연산은 gpu core 수가 충분하다면 시퀀스가 아무리 길든(n이 아무리 크든), query 및 key 벡터의 차원이 아무리 크든(d가 아무리 크든) gpu가 가장 특화된 행렬 연산의 병렬화를 통해 core 수가 무한정 많다는 전제 하에 한번에 계산 가능하다. 그래서 sequential operation의 경우 O(1)이 된다.

• 반면 RNN은 O($n$ $\cdot$ $d^2$)이다.
  
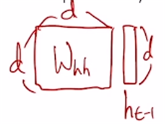
  vanilla RNN의 경우 위와 같이 d-차원의 벡터를 받아 d x d 행렬과 곱하여 d-차원의 벡터를 출력으로 내어주기 때문에 $d^2$번의 계산을 한다. 이것을 매 타임스텝마다 수행하므로 타임스텝 개수인 $n$에 $d^2$만큼의 곱만큼의 계산이 필요하다.

• 메모리 관점에서 볼 때, forward propagation, backpropagation 과정에서 발생하는 정보를 모두 다 메모리에 저장하고 있어야 backprop 과정에서 gradient를 계산할 때 저장한 값들을 사용할 수 있다.

• d라는 값은 임의로 정할 수 있는 하이퍼파라미터이다.
  그러나 n은 입력 데이터의 시퀀스가 길수록 우리가 임의로 고정된 값을 사용할 수 잇는 게 아니라서 가변값이 된다.
  따라서 RNN에서는 O($n$ $\cdot$ $d^2$)이지만 셀프 어텐션은 O($n^2$ $\cdot$ $d$)이므로 n의 값이 클 경우 셀프 어텐션이 RNN에서보다 훨씬 많은 메모리량을 필요로 한다. 즉 모든 쿼리와 모든 키 벡터들 간의 내적 값을 다 저장하고 있어야 하므로 메모리 양이 많이 필요하다.

(2) Seqeuntial Operation

• 이번에는 병렬화 측면에서 RNN와 self-attention을 보자. self-attention은 시퀀스 길이가 아무리 길더라도 gpu core 수가 충분히 뒷받침된다면 모든 계산을 동시에 수행할 수 있다. 따라서 복잡도는 O(1)이다.
• 그러나 RNN은 $h_{t-1}$을 계산해야만 재귀적으로 $h_t$를 계산할 수 있으므로 구조 상 병렬화가 불가능하다. 또한 backprop도 sequential해서 병렬화 불가하다. 따라서 sequential operation이 O(n)만큼의 복잡도를 가짐.
• 따라서 셀프 어텐션 모듈은 RNN보다 학습 속도는 빠르고 메모리 요구량은 많다.

(3) Maximum Path Length

• Lonng-term dependency와 직접적으로 관련이 있다. 최대 얼만큼의 타임스텝을 지나야 하는지를 의미한다.
• RNN의 경우 시퀀스의 가장 끝에 있는 단어가 가장 첫 단어의 정보를 참조할 경우 n만큼의 타임스텝을 지나야 하므로 O(n).
• Self-attention은 어텐션에 기반한 유사도를 계산함으로써 정보를 한 번에 얻기 때문에 long-term dependency 문제를 한번에 해결한다.
  
  

4. Block-Based Model